сибирский федеральный университет
 Скачать 337.72 Kb. Скачать 337.72 Kb.
|
                                 Федеральное государственное автономное Федеральное государственное автономноеобразовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Политехнический институт Кафедра электротехнических комплексов и электроэнергетических систем РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ по Теоретическим основам электротехники Вариант 3 Преподаватель ________ В.П.Довгун Студент гр.№ ФЭ17-03Б, 071722883 ________ В.Д. Вохмин Красноярск 2018 Расчетно-графическое задание № 1 Анализ резистивных цепей постоянного тока Для схемы, соответствующей номеру варианта, выполнить:
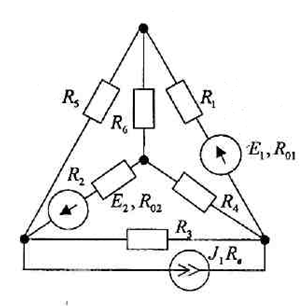 Задание 1 Записать уравнения по законам Кирхгофа. Решив полученную систему уравнений, определить токи и напряжения ветвей. Решение:
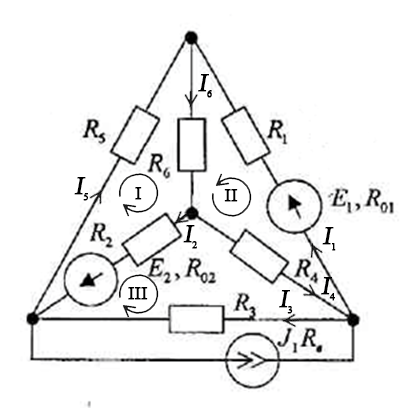
-I3+I2-I5=J I5+I1-I6=0 I6-I2-I4=0
I2R2+I5R5+I6R6=E2 I4R4+I1R1+I6R6=E1 I4R4+I3R3-I2R2= -E2
-I3+I2-I5=J I5+I1-I6=0 I6-I2-I4=0 I2R2+I5R5+I6R6=E2 I4R4+I1R1+I6R6=E1 I4R4+I3R3-I2R2=-E2
I1= 3,37 А I2=4,83 А I3=-2,6 А I4= -1,24 А I5=0,23 А I6=3,6 А
U12= I5R5=0,23×16= 3,67 В U23= I6R6=3,6×5=18 В U34= I4R4=1,24×7=8,65 В U42= I1R1- E1=3,67×18-70= -9,36 В U14= -I3R3=-2,6×5=13,02 В U31= I2R2- E2=4,83×10-70=-21,7 В
-2,6+4,83-0,23=2 0,23+3,37-3,6=0 3,6-4,83-(-1,24)=0 48,3+3,67+18=70 8,65+66,06+18=70 8,65-13,02-48,3=-70 Задание 2 Составить узловые уравнения цепи в матричной форме. Решив составленные уравнения, рассчитать токи во всех ветвях исходной цепи. Решение:
[Gy]*[ ��]=[J]
�� = Примем ��4=0
J =
I1=(��4-��2+E1)/R1=3,37 А I2=(��3-��1+E2)/R2=4,83 А I3=(��4-��1)/R3=-2,6 А I4=(��3-��4)/R4=-1,23 А I5=(��1-��2)/R5=0,23 А I5=(��2-��3)/R6=3,6 А Задание 3 Рассчитать ток в ветви с резистором 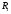 методом эквивалентного генератора. методом эквивалентного генератора.Решение:
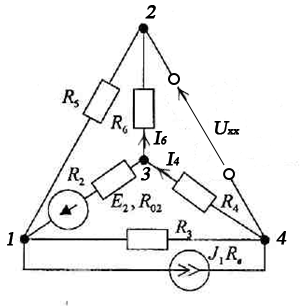 Eэкв=Uхх, где Uхх=I4R4+I6R6
J11= ��1G11-��3G13 J33=-��1G31+��3G33 , где G11=(1/(R5+R6))+(1/R2)+(1/R3)=0,348 Ом G13=G31=(1/(R5+R6))+(1/R2)=0,148 Ом G33=(1/(R5+R6))+(1/R2)+(1/R4)=0,29 Ом
J11=(E2/R2)-J1=5 А J33=-(E2/R2)=-7 А Тогда: I4=(��4-��1)/R4=3,06 А I6=(��3-��1)/(R5+R6)=-1,27 А Uхх=I4R4+I6R6=15,05 В
Преобразуем треугольник 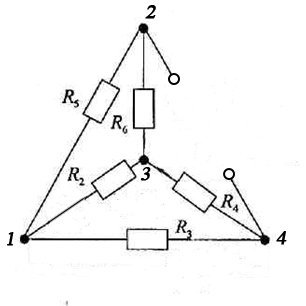 В звезду 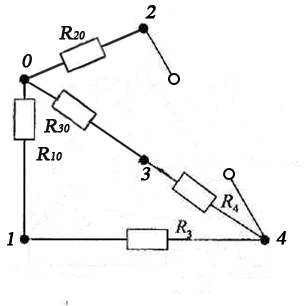 R20=(R5R6)/(R2+R5+R6)=2,58 Ом R30=(R2R6)/(R2+R5+R6)=1,61 Ом R10=(R2R5)/(R2+R5+R6)=5,16 Ом Тогда Rэкв=R20+(R4+R30)(R3+R10)/(R4+R30+R10+R3)=7,24 Ом Исходный ток I1=(E1+Eэкв)/(R1+Rэкв)=3,37 А Задание 4 Результаты расчетов свести в таблицу. Решение:
Задание 5 Составить баланс мощностей в исходной схеме (схеме с источниками напряжения и источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (мощность резистивных элементов). Решение:
∑Pист=∑Pнагр , где ∑Pист=E1I1+E2I2+Uj1J1
Uj1=I3R3+JRв=-7,02 В
∑Pист=560,2 Вт ∑Pнагр=I12R1+I22R2+I32R3+I42R2+I52R5+I62R6+J2Rв=560,17 Вт 560,2 Вт≈ 560,17 Вт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

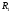 методом эквивалентного генератора.
методом эквивалентного генератора.