нирдарот. Документ 246 (2). Симметрическая группа
 Скачать 146.21 Kb.
|
6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановокПусть  — конечное множество из  элементов:  .Симметрическая группа  степени — группа всех биекций (взаимно-однозначных отображений)  множества в себя:  . Число элементов (подстановок) симметрической группы:  (число перестановок из ). Каждая биекция называется подстановкой (перестановкой) и записывается (природа элементов множества нас не интересует, значит можно считать, что элементы  — числа): Во второй строке записаны номера тех элементов, которым сопоставляются элементы из первой строки:  . Поэтому в написанной матрице столбцы можно как угодно переставлять, подстановка останется той же.Произведение двух подстановок  и  — результат проведения сначала первой из них, а затем второй (композиция отображений):  .Для этого представляют столбцы так, чтобы её первая строка совпадала со второй строкой ; тогда 1-ая строка есть первая строка  , а вторая строка — есть вторая строка .Некоторые математики иначе определяют произведение двух подстановок:  . (Это связано с тем, что произведение подстановок, по существу, означает композицию отображений, а математики не пришли к общему соглашению насчёт обозначения композиции отображений.) Соответственно, из-за этого меняется порядок умножения, в итоге результаты разнятся. Поэтому необходимо заранее обозначать композицию так, как будете её использовать.Пример. В данном примере показывается сама суть умножения подстановок. Первая строка первой подстановки «взаимно-однозначно отображается на» вторую строку второй подстановки. 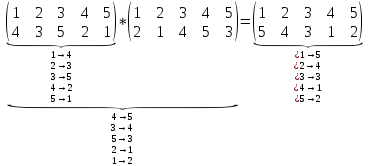 Пример.  Очевидно, что умножение перестановок ассоциативно, но не коммутативно. Нейтральный элемент — это тождественная подстановка  .Обратный к  это  , так как  .Таким образом, множество подстановок -го порядка — множество, на котором введена замкнутая ассоциативная бинарная операция «умножение», на этом множестве есть нейтральный элемент, и все элементы этого множества обратимы, следовательно, множество подстановок образует мультипликативную группу. Эта группа называется симметрической группой степени и обозначается . Очевидно, что это конечная группа, и что порядок этой группы (число её элементов) равен .Примеры. Запишем все  элементов (подстановок) симметрической группы  : ; Найти  и  :  Как видим  , то есть умножение подстановок некоммутативно.Найти обратную подстановку к  и проверить:  7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа ЦиклЦикл длины  — симметрическая группа степени , в которой элементы перемещены так, что  (или, что то же самое,  ), где все числа — разные,  . Цикл обозначается следующим образом: или  Причём набор таких элементов называется орбитой любого из чисел .Цикл независим, если у него нет общих чисел. Цикл длины 1 — это, очевидно, тождественная подстановка  ; в произведениях подстановок их можно не записывать.Теорема. Любую подстановку в можно записать в виде произведения независимых циклов. Разложение подстановки в произведение циклов длины  определено однозначно с точностью до порядка циклов.Доказательство. Очевидно, что отношение между числами «принадлежность одной -орбите» есть отношение эквивалентности:Рефлексивно, то есть  .Симметрично, то есть  .Транзитивно, то есть  .Данное отношение разбивает множество на классы эквивалентности по этому отношению. Каждый элемент принадлежит одному и только одному классу эквивалентности. Поэтому все числа  однозначно разбиваются на непересекающиеся классы эквивалентных между собой орбит, а подстановка представляется как произведение соответствующих циклов. Теорема доказана.Пример.  .Транспозиция — подстановка вида  , где  , сводящаяся к перестановке двух чисел между собой, или, что тоже самое, цикл длины 2.Любой цикл можно написать в виде произведения транспозиций:  Замечание. Транспозиции не коммутируют (как и перестановки). Пример.  .Пример.  .Пример.  .Пример.  .Нетрудно показать, что любую подстановку можно представить в виде произведения транспозиций. Такое представление не единственно (например, в примерах выше  ).Все подстановки подразделяются на 2 класса: чётные и нечётные. Если в матрице подстановки есть 2 столбца  , для которых  и  или  и  , то такая пара столбцов называется инверсией подстановки.Подстановка называется чётной или нечётной в зависимости от того, чётно или нечётно число инверсий в ней. Очевидно, что любая транспозиция является нечётной подстановкой: 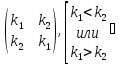 одна инверсия  нечётнаяТеорема. Если подстановка чётная, то при любом способе разложения её в произведение транспозиций число множителей (то есть транспозиций) чётно, а если нечётная — то число этих транспозиций нечётно. Следствие. Так как при перемножении чётных подстановок, очевидно, снова получается чётная подстановка, то множество всех чётных подстановок является подгруппой симметрической группы и называется знакопеременной группой и обозначается  . Причём порядок равен  .  состоит из одной подстановки: .  состоит из  подстановок и т. д.Пример. Подгруппа 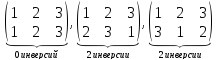симметрической группы состоит из 3-х подстановок: Произведение двух нечётных подстановок, очевидно, есть чётная подстановка, поэтому нечётные подстановки не образуют группу. Порядок подстановки — это наименьшее целое положительное число такое, что  .Пример. Докажем, что порядок подстановки  равен 5:  Теорема. Порядок подстановки равен НОК длин всех её независимых циклов. Также нетрудно показать, что порядок цикла равен длине цикла. Пример. Определить, является ли подстановка чётной или нечётной и разложить её в произведение транспозиций:  Сосчитаем число инверсий  . Инверсии — это пары столбцов , , , , , , . Поэтому (подстановка нечётная).Разложим её на циклы: Как видим, число транспозиций в произведении равно 5, то есть нечётно. Обратная операция: добавлена в середину только потому, что она равна . Другие подстановки (не равные ) в любое место добавлять нельзя, так как коммутативности нет. Порядок подстановки: . То есть . Проверим это. |