практика. Практикалық 1. Сиплекс дісі
 Скачать 22.82 Kb. Скачать 22.82 Kb.
|
|
Практикалық сабақ №1 Сызықтық программалаудың негізгі есебі. Жұмыстың мақсаты: есептерді шығару Сиплекс әдісіМысал Қойылған шектеулерде: x1 + x4 -2x5 =1, x2 -2x4 + x5 =2, x3+3x4 +x5 =3 сызықтық форманы L = -x4 +x5 минимумде: Шешу: Берілген жүйе ұйлесімді, себебі жүйенің матрицасы мен кеңейтілген матрица рангтары бідей және 3-ке тең.  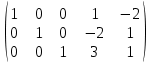 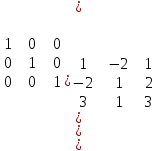 Салдарында үш базистық айнымалыларын қалған екі бос айнымалылары арқылы өрнектеуге болады. Біз x1, x2, x3 айнымалыларды x4, x5 арқылы өрнектейміз: 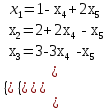 () ()Сызықтық форманы бос айнымалылар арқылы өрнектейміз: L = -x4 +x5 (есептің берілгені бойынша өрнектелген) Енді x4 =0, x5 =0 мәндеріндегі базистық айнымалылардың мәндерін табайық x1 =1, x2 =2 x3 =3 x4 =0, x5 =0 немесе (1,2,3,0,0). Бұл нүктедегі сызықтық форманың мәні L1 =0. Енді L форманың мәнін жоғарлатайық. x4 Мәнін өсірсек L мәні азаяды, себебі x4 таңбасы теріс, ал x5 мәнімен бірге форманың да мәні өседі. x5 мәнін x1 , x2 , x3 мәндері теріс болмайтындай және x4=0 ғылып өсірейік. () жүйесінің екінші теңдеуінен x5-тің мәнін 2-ге дейін көтеруге болатынын көреміз. Салдарында келесі мәндерге келеміз: x1 =5, x2 =0, x3 =1, x4 =0, x5=2 немесе (5,0,1,0,2). Бұл нүктедегі сызықтық форманың мәні L2=2 яғни өсті. Осы мақсатта жүйенің екінші теңдеуінен арқылы өрнектейміз: 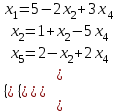 () ()L =2 -x2 +x4 L мәнін өсіру үшін x4 мәнін өсірейік. (**) жүйенің екінші теңдеуінен x3 теріс емес шартында x4 -ті x4=1/5 мәніне дейін өсіруге болатынын көреміз. Олай болса жаңа мұмкін шешімі x1 =28/5, x2=0 x3 =0, x4 =1/5, x5 =12/5 немесе (28/5,0,0,1/5,12/5) болады. Сызықтық форма мәні мұнда L3 =11/5. Келесі қадамда бос айнымалы ретінде x2, x3 алайық. Олар табылған шешімде нөлге тең. x1 , x4 , x5айнымалылары былай өрнектеледі: 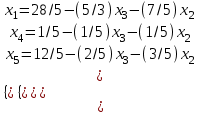 (***) (***)L = 11/5-(1/5)x3 –(4/5)x2 Соңғы формада айнымалылардың екеуіде теріс таңбамен болғандықтан L дің ең үлкен мәні xә =0, xі =0 мәндерінде қабылданады. Демек, (28/5,0,0,1/5,12/5) шешімі тиімді болады: Lmax = 11/5. №1 Берілген шектеулерде L(x)=12x1 +4x2сызықтық форманы минимумдау қажет. x1 + x2 2, x1³1/2, x2 4, x1 - x2£ 0 Шешу: x1 + x2 = 2, x1 =1/2, x2 = 4, x1 - x2 = 0 түзулермен шектелген облысты құрып, С(12,4) векторын сызайық. Осы вектордың бойымен L(x) түзуі оң бағытта жылжыса, оның мяні өседі, кері бағытта – кемиді. Осы себепте, оталған облясқа алғашқы кіріс нүктесінде сызықтық форманың – ең кіші, ал шығу нүктесінде – ең улкен мәні қабылданады. №2 Берілген шектеулердеL(x)=2x1 +2x2 сызықтық форманы минимумдау қажет 3x1 - 2x2³ -6, 3x1 + x2³ 3, x1£ 3 №3 Берілген шектеулердеL(x)=x1 +3x2+ x3 сызықтық форманы минимумдау қажет x2 + x3£ 3, x1 - x2³ 0 3x1 + x2£ 15, x2³ 1 №4 Берілген шектеулердесызықтық форманы минимумдау қажет L(x)=3x1 -6x2 + 2x3 3x1 + 3x2 + 2x3 £ 6, x1 + 4x2 +8x3 £ 8 |
