Лебедев О.И. ЛТ-019-з КР 9 вариант. Система уравнений по законам Кирхгофа

• Название: Система уравнений по законам Кирхгофа
• Дата: 24.03.2022
• Размер: 238.33 Kb.
• Имя файла: Лебедев О.И. ЛТ-019-з КР 9 вариант.docx
• Тип: Закон; #413736

Задание 1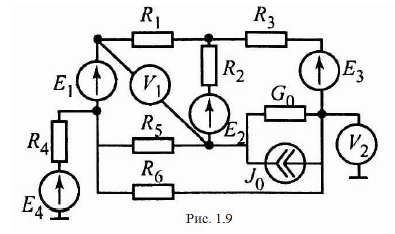



Рис. 1. Заданная цепь.

Исходные данные: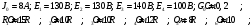



В ветви 4 тока нет, поэтому, в дальнейшем расчёте её не учитываем.



Рис. 2. Заданная цепь с выбранным направлением токов.

Система уравнений по законам Кирхгофа.

Цепь содержит У=4 узла и В=6 ветвей, не содержащих источника тока. Необходимое количество уравнений первого закона Кирхгофа: N_I=У-1=3. Необходимое количество уравнений второго закона Кирхгофа: N_II=В-У+1=3. Составляем эти уравнения: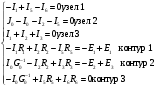



Расчёт методом узловых потенциалов.

Рассчитываем токи методом узловых потенциалов. Принимаем потенциал узла 0 равным нулю. Для остальных узлов составляем систему узловых уравнений: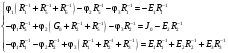



После подстановки получаем: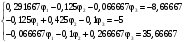



Отсюда определяем узловые напряжения: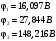



Далее определяем токи в ветвях схемы: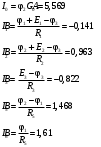



Напряжение на источнике тока: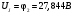



Проверка (узел 1):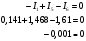



Расчёт токов методом контурных токов.

Составляем систему контурных уравнений: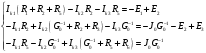



После подстановок получаем систему уравнений: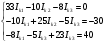



Из системы уравнений определяем контурные токи: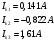



Далее определяем токи в ветвях: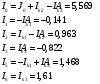



Токи, рассчитанные методом контурных токов, практически полностью совпали с токами, рассчитанными методом узловых потенциалов.

Рассчитываем показания вольтметров: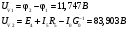



Расчёт баланса мощностей.

Мощность источников энергии: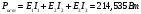



Мощность потребителей энергии: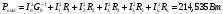



Мощность потребителей в точности совпала с мощностью источников.

Построение потенциальной диаграммы внешнего контура и определение точки заземления

Определяем потенциалы узлов: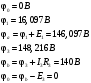





Рис. 3. Потенциальная диаграмма внешнего контура

Выбираем точку внешнего контура соединения с корпусом устройства таким образом, чтобы разность потенциалов между этой точкой и любой другой точкой внешней цепи была минимальной. Этому условию удовлетворяет точка "1".

Расчёт тока 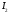методом эквивалентного генератора.

Методом контурных токов определим ток короткого замыкания. Составляем систему контурных уравнений (без резистора ):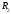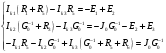



После подстановок получаем систему уравнений: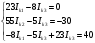



Отсюда определяем контурные токи и ток короткого замыкания: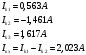



Методом узловых напряжений определим напряжение холостого хода. Составляем систему контурных уравнений (без второй ветви):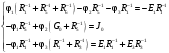



После подстановки получаем: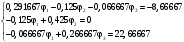



Отсюда определяем узловые напряжения и напряжение холостого хода: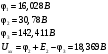



Внутреннее сопротивление эквивалентного генератора: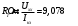



Ток в ветви: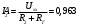



Задание 2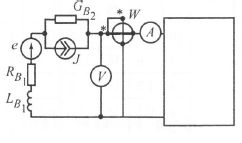



Рис. 4. Схема цепи.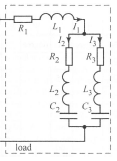



Рис. 5. Схема нагрузки.

Исходные данные: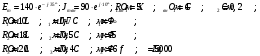

1. 
   Определяем реактивные сопротивления ветвей нагрузки: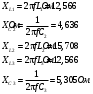
   

2. 
   Определяем полные комплексные сопротивления ветвей: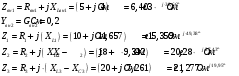
   

3. 
   Определим полное сопротивление нагрузки: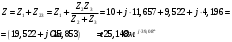
   

4. 
   Составляем расчётную схему (рис. 6)
   

Рис. 6. Схема замещения

5. 
   Определяем токи в схеме замещения методом узловых потенциалов.
   

Составляем систему узловых уравнений: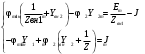



После подстановки получаем: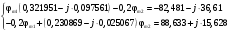



Определяем узловые потенциалы: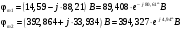



Определяем токи в схеме замещения: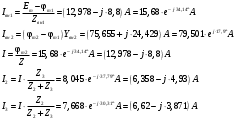



Напряжение на источнике тока: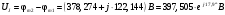



Падения напряжения на сопротивлениях нагрузки: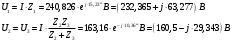



Падение напряжения на нагрузке: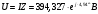



Падение напряжение на внутреннее сопротивление источника ЭДС: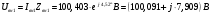

6. 
   Определяем показания приборов: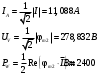
   

7. 
   Составляем баланс мощностей.
   

Мощность источников энергии: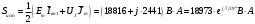



Активная и реактивная мощности источников: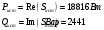



Коэффициент мощности: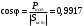



Мощность приёмников энергии: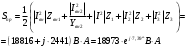



Активная и реактивная мощности приёмников: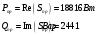



Активная и реактивная мощности приёмников и источников совпали. Следовательно, расчёт выполнен верно.

8. 
   Строим векторную диаграмму.
   

• 
  На комплексной плоскости строим векторы токов и составляем в векторной форме уравнения 1-гозакона Кирхгофа: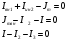
  

• 
  В векторной форме составляем уравнение 2-го закона Кирхгофа: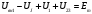
  

Рис. 7. Векторная диаграмма токов и напряжений.

9. 
   Мгновенные значения тока, напряжения и мощности на нагрузке.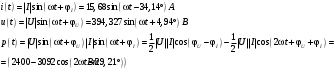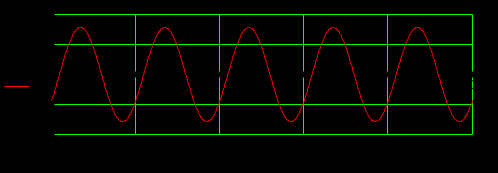
   

Рис. 8. График тока в нагрузке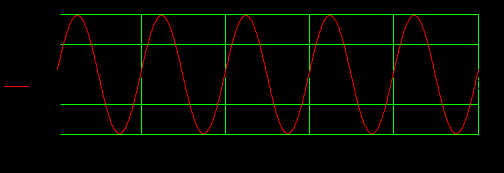



Рис. 9. График напряжения на нагрузке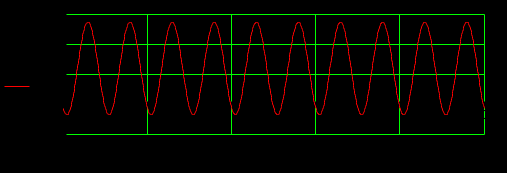



Рис. 10. График активной мощности в нагрузке.