Лаба 1. Билеты. Системы и языки программирования система программирования

Название	Системы и языки программирования система программирования
Анкор	Лаба 1
Дата	04.11.2022
Размер	0.78 Mb.
Формат файла
Имя файла	Билеты .docx
Тип	Документы #770452
страница	2 из 3

1 2 3

Алфавит[править | править код]

Современные языки программирования рассчитаны на использование ASCII, то есть доступность всех графических символов ASCII является необходимым и достаточным условием для записи любых конструкций языка.
Семантика языка — это смысловое значение слов. В программировании — начальное смысловое значение операторов, основных конструкций языка и т. п.

Пример:

Первый код:

i=0; while(i<5){i++;}

Второй код:

i=0; do{i++;} while(i<=4);
Синтаксис языка программирования — набор правил, описывающий комбинации символов алфавита, считающиеся правильно структурированной программой (документом) или её фрагментом. Синтаксису языка противопоставляется его семантика. Синтаксис языка описывает «чистый» язык, в то же время семантика приписывает значения (действия) различным синтаксическим конструкциям.

Каждый язык программирования имеет синтаксическое описание как часть грамматики.

18. СПОСОБЫ ОПИСАНИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ. ТРАНСЛЯЦИЯ.
Спецификация — это максимально точное определение языка, его синтаксиса и семантики. Спецификация — весьма строгий и сухой документ, который не может служить учебником по программированию. Она обычно содержит не слишком много примеров, не дает рекомендаций по применению тех или иных конструкций, а лишь определяет их форму и смысл.
Средства описания языков программирования. Как уже указывалось, язык программирования должен иметь алфавит, синтаксис и семантику. Правила, определяющие структуру текста, составляют синтаксис (грамматику). Правила, позволяющие извлекать из текста смысл, называются семантикой языка.

Для описания синтаксиса языка используется так называемый метаязык (язык для описания языка). В качестве метаязыка используют либо металингвистические формулы Бэкуса—Наура, либо синтаксические диаграммы. Джон Бэкус разработал специальную систему определений для языков программирования. Например, определяя элемент «цифра», он указывал:

<цифра> ::=0|1|2|3|4|5|6|7|8|9.

Этот способ записи назвали нормальной формой Бэкуса, или БНФ. Датский астроном П. Наур внес некоторые уточнения, и форму стали называть формой Бэкуса—Наура, но сокращенное название БНФ осталось.

В БНФ каждое понятие определяется с помощью одной металингвистической формулы, в левой части которой указываются определяемые понятия, а в правой — описываются все допустимые структуры языка, соответствующие этому понятию. Левая и правая части формулы связываются знаком ::=, который читается «по определению есть». При перечислении дополнительных вариантов структур в правой части используется знак |, имеющий смысл «или». Все определяемые понятия языка программирования заключаются в угловые скобки < >, а неопределяемые исходные понятия языка называются лексемами. Лексемы могут использоваться в правой части формулы.

Например, определить понятие <целое число>, если алфавит языка программирования включает арабские цифры и знаки арифметических операций. Сначала определим понятие <циф- ра> (см. ранее). Затем введем понятие <целое без знака>, описав его следующей формулой:

<целое без знака> ::= <цифра> | <целое без знака> <цифра>
Трансля́тор — программа или техническое средство, выполняющее трансляцию программы^[1][2].

Компиляция и интерпретация.

Трансля́ция програ́ммы — преобразование программы, представленной на одном из языков программирования, в программу, написанную на другом языке. Транслятор обычно выполняет также диагностику ошибок, формирует словари идентификаторов, выдаёт для печати текст программы и т. д.^[1]

Язык, на котором представлена входная программа, называется исходным языком, а сама программа — исходным кодом. Выходной язык называется целевым языком.

Существует несколько видов трансляторов^[2].

Диалоговый транслятор — транслятор, обеспечивающий использование языка программирования в режиме разделения времени.
Синтаксически-ориентированный (синтаксически-управляемый) транслятор — транслятор, получающий на вход описание синтаксиса и семантики языка, текст на описанном языке и выполняющий трансляцию в соответствии с заданным описанием.
Однопроходной транслятор — транслятор, преобразующий исходный код при его однократном последовательном чтении (за один проход).
Многопроходной транслятор — транслятор, преобразующий исходный код после его нескольких чтений (за несколько проходов).
Оптимизирующий транслятор — транслятор, выполняющий оптимизацию создаваемого кода. См. оптимизирующий компилятор.

Цель трансляции — преобразование текста с одного языка на язык, понятный адресату. При трансляции компьютерной программы адресатом может быть:

устройство — процессор (трансляция называется компиляцией);
программа — интерпретатор (трансляция называется интерпретацией).

Виды трансляции:

компиляция;
в исполняемый код
в машинный код
в байт-код

Достоинства компиляции:

компиляция программы выполняется один раз;
наличие компилятора на устройстве, для которого компилируется программа, не требуется.

Недостатки компиляции:

компиляция — медленный процесс;
при внесении изменений в исходный код, требуется повторная компиляция.

Интерпретация — процесс чтения и выполнения исходного кода. Реализуется программой — интерпретатором.

Интерпретатор может работать двумя способами:

читать код и исполнять его сразу (чистая интерпретация^[6]);
читать код, создавать в памяти промежуточное представление кода (байт-код или p-код), выполнять промежуточное представление кода (смешанная реализация^[6]).

В первом случае трансляция не используется, а во втором — используется трансляция исходного кода в промежуточный код.

Интерпретатор моделирует машину (виртуальную машину), реализует цикл выборки-исполнения команд машины. Команды машины записываются не на машинном языке, а на языке высокого уровня. Интерпретатор можно назвать исполнителем языка виртуальной машины.
Достоинства интерпретаторов по сравнению с компиляторами:

возможность работы в интерактивном режиме;
отсутствие необходимости перекомпиляции исходного кода после внесения изменений и при переносе кода на другую платформу.

Недостатки интерпретаторов по сравнению с компиляторами:

низкая производительность (машинный код исполняется процессором, а интерпретируемый код — интерпретатором; машинный код самого интерпретатора исполняется процессором);
необходимость наличия интерпретатора на устройстве, на котором планируется интерпретация программы;
обнаружение ошибок синтаксиса на этапе выполнения (актуально для чистых интерпретаторов).

19. ТИПЫ ДАННЫХ, СПОСОБЫ ЗАДАНИЯ ТИПА. КОНСТАНТЫ И ПЕРЕМЕННЫЕ. ИДЕНТИФИКАТОРЫ.
Тип данных (тип) — множество значений и операций над этими значениями

Тип данных характеризует одновременно:

множество допустимых значений, которые могут принимать данные, принадлежащие к этому типу;
набор операций, которые можно осуществлять над данными, принадлежащими к этому типу.

По другой классификации типы делятся на самостоятельные и зависимые. Важными разновидностями последних являются ссылочные типы, частным случаем которых, в свою очередь, являются указатели. Ссылки (в том числе и указатели) представляют собой несоставной зависимый тип, значения которого являются адресом в памяти ЭВМ другого значения.

Логический тип

Целочисленные типы

Числа с плавающей запятой

Строковые типы

Идентификационные типы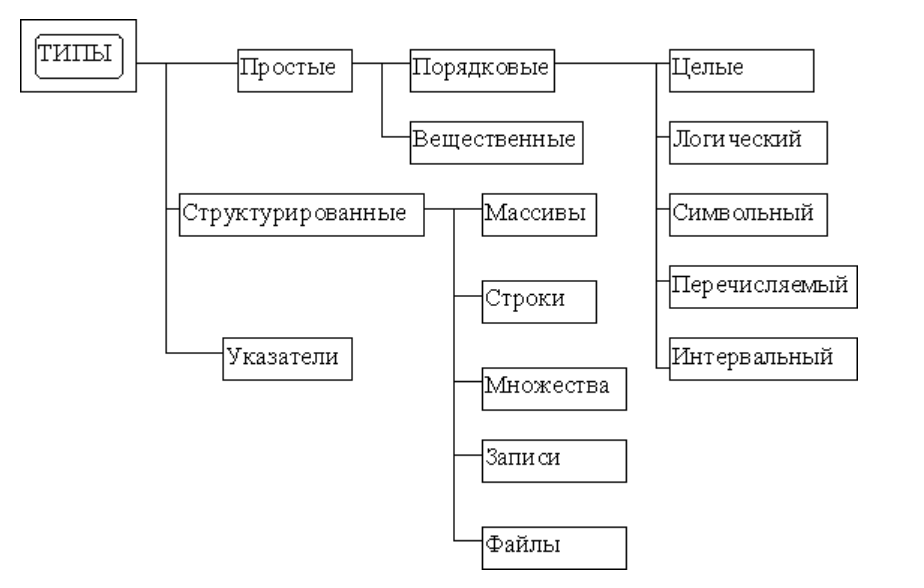

Идентификатором является последовательность букв, цифр и знаков подчеркивания, которая начинается с буквы или символа подчеркивания и не содержит пробелов. Идентификаторы выступают в качестве имен констант, переменных, процедур, функций, модулей и др. Идентификатор может иметь произвольную длину, однако значимыми являются только 63 символа.
Переменной называют элемент программы, который предназначен для хранения, коррекции и передачи данных внутри программы.
Константа - это идентификатор, обозначающий некоторую неизменную величину определенного типа. Константы, как и переменные, должны объявляться в соответствующем разделе программы.
Целочисленные константы.

Вещественные константы.

Строковые константы.
symb = '?'; apostroph =''''; {символьная}

limit = 2.4E-10; {вещественная с показателем степени}

money: real = 57.23; {типизированная вещественная}

20. СТРУКТУРИРОВАННЫЕ ТИПЫ ДАННЫХ. ВЫРАЖЕНИЯ, ОПЕРАЦИИ, ОПЕРАТОРЫ.
Структурированными данными называют такие данные, которые состоят из других типов данных. Структурированные типы данных определяют наборы однотипных или разнотипных компонент. К ним относятся, в частности, переменные типов: Array - массивы (табличные данные); String – строковые величины; Record – данные типа запись; Set – данные типа множество; File – данные типа файл.
Массивы – это набор значений одного типа. Они удобны, когда нам нужно что-то перечислить.
Выражения

Программа оперирует с данными. Числа можно складывать, вычитать, умножать, делить. Из разных величин можно составлять выражения, результат вычисления которых – новая величина. Приведем примеры выражений:

X * 12 + Y // значение X умножить на 12 и к результату прибавить значение Y

val < 3 // сравнить значение val с 3

-9 // константное выражение -9

Выражение, после которого стоит точка с запятой – это оператор-выражение. Его смысл состоит в том, что компьютер должен выполнить все действия, записанные в данном выражении, иначе говоря, вычислить выражение.

x + y – 12; // сложить значения x и y и затем вычесть 12

a = b + 1; // прибавить единицу к значению b и запомнить результат в переменной a

Выражения – это переменные, функции и константы, называемые операндами, объединенные знаками операций. Операции могут быть унарными – с одним операндом, например, минус; могут быть бинарные – с двумя операндами, например сложение или деление.

С помощью операторов можно складывать, вычитать и делать много других операций с переменными. Операторами являются +, -, *, / и другие. Да даже; является оператором, говорящим, что выражение завершено.
Оператор — это элемент языка, задающий полное описание действия, которое необходимо выполнить. Каждый оператор представляет собой законченную фразу языка программирования и определяет некоторый вполне законченный этап обработки данных.
После того как мы записали наше выражение, например сложения,
int a = 127;

int b = -12;

a + b;

Операция присваивания

Присваивание – это тоже операция, она является частью выражения. Значение правого операнда присваивается левому операнду.

x = 2; // переменной x присвоить значение 2

cond = x < 2; // переменной cond присвоить значение true, если x меньше 2,

// в противном случае присвоить значение false

3 = 5; // ошибка, число 3 неспособно изменять свое значение

Последний пример иллюстрирует требование к левому операнду операции присваивания. Он должен быть способен хранить и изменять свое значение. Переменные, объявленные в программе, обладают подобным свойством. В следующем фрагменте программы
Выражение задаёт порядок выполнения действий над данными и состоит из операндов (констант, переменных, обращений к функциям), круглых скобок и знаков операций. Операции делятся на унарные (например, -с) и бинарные (например, а+b)
21. АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ОПЕРАТОРЫ. ПРОГРАММИРОВАНИЕ ВВОДА И ВЫВОДА ИНФОРМАЦИИ.
Основными арифметическими операциями являются: сложение ('+'), вычитание ('-'), умножение ('*') и деление ('/'). Порядок выполнения операций в выражении соответствует их приоритету. Операции с одинаковым приоритетом в выражении выполняются слева направо.
Среди логических операций следует выделить операции 'и' ('and'), 'или' ('or'), отрицание 'не' ('not') и сложение по модулю 2 ('xor'). В языке Си логические операции обозначаются следующим образом: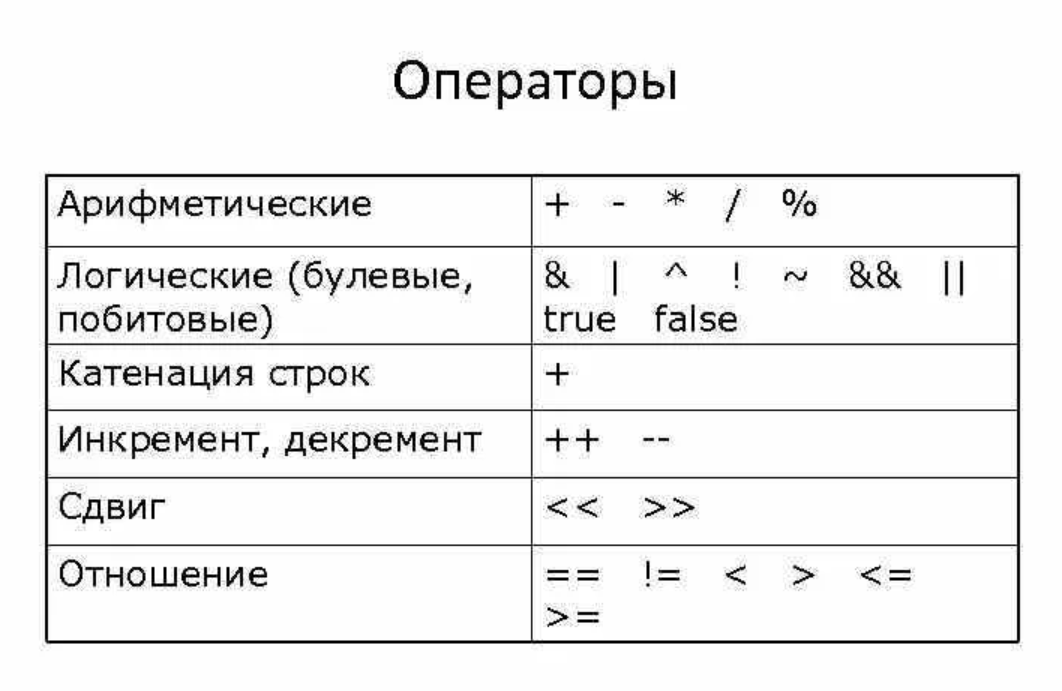

В С++ определены следующие логические операции || (или), && (и), ! (не). Логические операции выполняются над логическими значениями true (истина) и false (ложь). В языке С ложь — 0, истина — любое значение

0. В таблице 2.6 приведены результаты логических операций
Функции и операторы ввода/вывода информации

	Библиотека stdio.h	Библиотека iostream
Вывод	Функция printf();	Оператор cout
Ввод	Функция scanf();	Оператор cin

22. ПОДПРОГРАММЫ, МЕТОДЫ ПЕРЕДАЧИ ПАРАМЕТРОВ ПРИ ИСПОЛЬЗОВАНИИ ПОДПРОГРАММ. ОСНОВЫ ОБЪЕКТНО-ОРИЕНТИРОВАННОГО ПРОГРАММИРОВАНИЯ. ИНКАПСУЛЯЦИЯ, НАСЛЕДОВАНИЕ, ПОЛИМОРФИЗМ.
Подпрограмма (англ. subroutine) — поименованная или иным образом идентифицированная часть компьютерной программы, содержащая описание определённого набора действий. Подпрограмма может быть многократно вызвана из разных частей программы. В языках программирования для оформления и использования подпрограмм существуют специальные синтаксические средства.
Подпрограммы изначально появились как средство оптимизации программ по объёму занимаемой памяти — они позволили не повторять в программе идентичные блоки кода, а описывать их однократно и вызывать по мере необходимости. К настоящему времени данная функция подпрограмм стала вспомогательной, главное их назначение — структуризация программы с целью удобства её понимания и сопровождения.

Выделение набора действий в подпрограмму и вызов её по мере необходимости позволяет логически выделить целостную подзадачу, имеющую типовое решение.

Даже в тех случаях, когда в подпрограмму выделяется однократно производимый набор действий, это оправдано, так как позволяет сократить размеры целостных блоков кода, составляющих программу, то есть сделать программу более понятной и обозримой.

Преимущества разбиения программы на подпрограммы включают:

Декомпозиция комплексной программной задачи на простые шаги: это один из двух основных инструментов структурированного программирования и структур данных
Уменьшение дублированного кода
Возможность повторного использования кода в других программах
Разделение крупной программной задачи между различными программистами, или различными стадиями проекта
Сокрытие деталей реализации от пользователей подпрограммы
Улучшение прослеживания

Существует несколько способов передачи параметров в подпрограмму.

Передача параметров по значению. Формальному параметру присваивается значение фактического параметра. В этом случае формальный параметр будет содержать копию значения, имеющегося в фактическом, и никакое воздействие, производимое внутри подпрограммы на формальные параметры, не отражается на параметрах фактических.

Передача параметров по ссылке. В формальный параметр может быть помещён сам фактический параметр (обычно это реализуется путём помещения в формальный параметр ссылки на фактический). При этом любое изменение формального параметра в подпрограмме отразится на фактическом параметре — оба параметра во время вызова подпрограммы суть одно и то же. Параметры, передаваемые по ссылке, дают возможность не только передавать параметры внутрь подпрограммы, но и возвращать вычисленные значения в точку вызова. Для этого параметру внутри подпрограммы просто присваивается нужное значение, и после возврата из подпрограммы переменная, использованная в качестве фактического параметра, получает это значение.

Передача параметров по имени. В формальный параметр может быть помещено произвольное выражение. При этом вычисление этого выражения произойдёт внутри подпрограммы в тот момент, когда потребуется его значение. Если это значение фигурирует несколько раз, то и вычисляться оно будет тоже несколько раз. Параметры, передаваемые по имени, дают возможность писать довольно универсальные подпрограммы. Такой способ передачи параметров используется, к примеру в языках Алгол или Алгол 68.

Передача параметров через стек. Это фактически разновидность передачи параметра по значению «с ручным приводом», в данном случае отсутствует понятие формальных и фактических параметров. Все параметры лежат на стеке, причём их типы, количество и порядок не контролируются компилятором. Данный подход реализован в языке Форт.

Основные принципы ООП.

Инкапсуляция - сокрытие реализации

Инкапсуляция – это свойство системы, позволяющее объединить данные и методы, работающие с ними, в классе и скрыть детали

реализации от пользователя.

Инкапсуляция неразрывно связана с понятием интерфейса класса. По сути, всё то, что не входит в интерфейс, инкапсулируется в классе.
Наследование - создание новой сущности на базе уже существующей.

Наследование – это свойство системы, позволяющее описать новый класс на основе уже существующего с частично или полностью заимствующейся функциональностью. Класс, от которого производится наследование, называется базовым или родительским. Новый класс – потомком, наследником или производным классом.
Необходимо отметить, что производный класс полностью удовлетворяет спецификации родительского, однако может иметь дополнительную функциональность. С точки зрения интерфейсов, каждый производный класс полностью реализует интерфейс родительского класса. Обратное не верно.
Действительно, в нашем примере мы могли бы произвести с новыми автомобилями все те же действия, что и со старым: увеличить или уменьшить скорость, повернуть, включить сигнал поворота. Однако, дополнительно у нас бы появилась возможность, например, включить противотуманные фонари.
Полиморфизм - возможность иметь разные формы для одной и той же сущности
Полиморфизм – это свойство системы использовать объекты с одинаковым интерфейсом без информации о типе и внутренней структуре объекта.
Например, если вы читаете данные из файла, то, очевидно, в классе, реализующем файловый поток, будет присутствовать метод похожий на следующий: byte[] readBytes( int n );

Предположим теперь, что вам необходимо считывать те же данные из сокета. В классе, реализующем сокет, также будет присутствовать метод readBytes. Достаточно заменить в вашей системе объект одного класса на объект другого класса, и результат будет достигнут.
При этом логика системы может быть реализована независимо от того, будут ли данные прочитаны из файла или получены по сети. Таким образом, мы абстрагируемся от конкретной специализации получения данных и работаем на уровне интерфейса. Единственное требование при этом – чтобы каждый используемый объект имел метод readBytes.

23. ШИФРЫ ЗАМЕНЫ И ПЕРЕСТАНОВКИ, ИХ СВОЙСТВА, КОМПОЗИЦИИ ШИФРОВ. КРИПТОСТОЙКОСТЬ ШИФРОВ, ОСНОВНЫЕ ТРЕБОВАНИЯ К ШИФРАМ.

Шифр простой замены

Очередной шифр, относящийся к группе одноалфавитных шифров подстановки. Ключом шифра служит перемешанный произвольным образом алфавит. Например, ключом может быть следующая последовательность букв: XFQABOLYWJGPMRVIHUSDZKNTEC.
При шифровании каждая буква в тексте заменяется по следующему правилу. Первая буква алфавита замещается первой буквой ключа, вторая буква алфавита — второй буквой ключа и так далее. В нашем примере буква A будет заменена на X, буква B на F.
При расшифровке буква сперва ищется в ключе и затем заменяется буквой стоящей в алфавите на той же позиции.

B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
b	e	x	g	w	i	q	v	l	o	u	m	p	j	r	s	t	n	k	h	f	y	z	a	d	c

Расшифровка – анализ частоты использования букв, триграммы ing, the, and и т.д.

Перестановочный шифр

Помимо шифров подстановки, широкое распространение также получили перестановочные шифры. В качестве примера опишем Шифр вертикальной перестановки.
В процессе шифрования сообщение записывается в виде таблицы. Количество колонок таблицы определяется размером ключа. Например, зашифруем сообщение WE ARE DISCOVERED. FLEE AT ONCE с помощью ключа 632415.
Так как ключ содержит 6 цифр дополним сообщение до длины кратной 6 произвольно выбранными буквами QKJEU и запишем сообщение в таблицу, содержащую 6 колонок, слева направо:

Для получения шифртекста выпишем каждую колонку из таблицы в порядке, определяемом ключом: EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE.
При расшифровке текст записывается в таблицу по колонкам сверху вниз в порядке, определяемом ключом.
1. Шифры перестановки

Определение преобразования - перестановка

Шифрование перестановкой заключается в том, что символы открытого текста переставляются по определенному правилу в пределах некоторого блока этого текста. Рассмотрим перестановку, предназначенную для шифрования сообщения длиной n символов. Его можно представить с помощью таблицы

где i₁ - номер места шифртекста, на которое попадает первая буква открытого текста при выбранном преобразовании, i₂ - номер места для второй буквы и т. д.

В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней те же числа, но в произвольном порядке. Такая таблица называется перестановкой степени n.

Зная перестановку, задающую преобразование, можно осуществить как шифрование, так и расшифрование текста. В этом случае, сама таблица перестановки служит ключом шифрования.

Число различных преобразований шифра перестановки, предназначенного для шифрования сообщений длины n, меньше либо равно n

Композиции шрифтов

Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т.е. последовательное шифрование исходного текста с помощью двух или более методов.

Стойкость комбинированного шифрования S не ниже произведения стойкостей используемых способов

S >= S1*S2*...*S_k

Виды комбинированных методов шифрования

· Подстановка+перестановка;

· Подстановка+гаммирование;

· Перестановка+гаммирование;

· Гаммирование+гаммирование.

Гаммирование –наложение гаммы (символы некоторой специальной последовательности) на исходный текст.
Циклические операции шифрования – несколько раз.
Криптостойкость шифров
Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять криптоанализу. Стойким считается алгоритм, успешная атака на который требует от атакующего обладания недостижимым на практике объёмом вычислительных ресурсов или перехваченных открытых и зашифрованных сообщений либо настолько значительных затрат времени на раскрытие, что к его моменту защищённая информация утратит свою актуальность.
Об абсолютной стойкости (или теоретической стойкости) говорят в случае, если криптосистема не может быть раскрыта ни теоретически, ни практически даже при наличии у атакующего бесконечно больших вычислительных ресурсов. Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено Клодом Шенноном и опубликовано в работе «Теория связи в секретных системах»^[1]. Там же определены требования к такого рода системам:

ключ генерируется для каждого сообщения (каждый ключ используется только один раз)
ключ статистически надёжен (то есть вероятности появления каждого из возможных символов равны, символы в ключевой последовательности независимы и случайны)
длина ключа равна или больше длины сообщения
исходный (открытый) текст обладает некоторой избыточностью (что является критерием оценки правильности расшифровки)

К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:

• достаточная криптостойкость (надежность закрытия данных);
• простота процедур шифрования и расшифрования;
• незначительная избыточность информации за счет шифрования;
• нечувствительность к небольшим ошибкам шифрования и др.

В той или иной мере этим требованиям отвечают:

• шифры перестановок;
• шифры замены;
• шифры гаммирования;
• шифры, основанные на аналитических преобразованиях шифруемых данных.

24. ТЕОРЕТИЧЕСКАЯ СТОЙКОСТЬ ШИФРОВ, СОВЕРШЕННЫЕ И ИДЕАЛЬНЫЕ ШИФРЫ.
Стойкость шифра – это способность шифра противостоять атакам на него. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов, недостижимого объёма перехваченных открытых и зашифрованных сообщений или же такого времени раскрытия, что по его истечению защищенная информация будет уже не актуальна, и т. д.

Теоретическая стойкость

При анализе теоретической стойкости шифров отвлекаются от объема реальных затрат на дешифрование. Основным критерием является возможность получения на основе шифртекста вероятностной информации об открытом тексте или используемом ключе. Для теоретически стойких (совершенных) шифров сама задача дешифрования становится бессмысленной.

Практическая стойкость

Центровым понятием в практической стойкости по Шеннону является рабочая характеристика шифра, представляющая собой средний объем работы W(N), необходимый для определения ключа по криптограмме, состоящей из N букв, причем N>L₀(объем перехвата перевалил за расстояние единственности), измеренный в удобных элементарных операциях.

Ценность большинства данных со временем снижается, поэтому важно, чтобы рабочая характеристика шифра превышала по стоимости защищаемую информацию.

Сложность взлома алгоритмов классифицируется по категориям:

· Полное вскрытие. Криптоаналитик находит ключ k, такой, что D_k(x)=y.

· Глобальная дедукция. Криптоаналитик находит альтернативный алгоритм A, эквивалентный D_k(x) без знания k.

· Случайная (или частичная) дедукция. Криптоаналитик находит (крадет) открытый текст для перехваченного шифрованного сообщения.

· Информационная дедукция. Криптоаналитик добывает некоторую информацию о ключе или открытом тексте. Такой информацией могут быть несколько битов ключа, сведения о форме открытого текста и пр.
Совершенные шифры по К. Шеннону

Об абсолютной стойкости (или теоретической стойкости) говорят в случае, если криптосистема не может быть раскрыта ни теоретически, ни практически даже при наличии у атакующего бесконечно больших вычислительных ресурсов. Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено Клодом Шенноном и опубликовано в работе «Теория связи в секретных системах»^[1]. Там же определены требования к такого рода системам:

ключ генерируется для каждого сообщения (каждый ключ используется только один раз)
ключ статистически надёжен (то есть вероятности появления каждого из возможных символов равны, символы в ключевой последовательности независимы и случайны)
длина ключа равна или больше длины сообщения
исходный (открытый) текст обладает некоторой избыточностью (что является критерием оценки правильности расшифровки)

Идеальный шифр – это шифр, который полностью скрывает в шифрованном тексте все статистические закономерности открытого текста. Схема шифрования называется абсолютно стойкой (безусловно защищенной), если шифрованный текст не содержит информации, достаточной для однозначного восстановления открытого текста.

25. БЛОКОВЫЕ ШИФРЫ. ПОТОКОВЫЕ ШИФРЫ.
Симметри́чные криптосисте́мы (также симметричное шифрование, симметричные шифры) (англ. symmetric-key algorithm) — способ шифрования, в котором для шифрования и дешифрования применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в тайне обеими сторонами, должны осуществляться меры по защите доступа к каналу, на всем пути следования криптограммы, или сторонами взаимодействия посредством криптообъектов, сообщений, если данный канал взаимодействия под грифом «Не для использования третьими лицами». Алгоритм шифрования выбирается сторонами до начала обмена сообщениями.
Алгоритмы шифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами. Главным принципом в них является условие, что передатчик и приемник заранее знают алгоритм шифрования, а также ключ к сообщению, без которых информация представляет собой всего лишь набор символов, не имеющих смысла.

Классическими примерами таких алгоритмов являются симметричные криптографические алгоритмы, перечисленные ниже:

Простая перестановка
Одиночная перестановка по ключу
Двойная перестановка
Перестановка «Магический квадрат»

Бло́чный шифр — разновидность симметричного шифра^[1], оперирующего группами бит фиксированной длины — блоками, характерный размер которых меняется в пределах 64‒256 бит. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Фактически, блочный шифр представляет собой подстановку на алфавите блоков, которая, как следствие, может быть моно- или полиалфавитной.^[2] Блочный шифр является важной компонентой многих криптографических протоколов и широко используется для защиты данных, передаваемых по сети.
Блочный шифр состоит из двух парных алгоритмов: шифрования и расшифрования.^[8] Оба алгоритма можно представить в виде функций. Функция шифрования E (англ. encryption — шифрование) на вход получает блок данных M (англ. message — сообщение) размером n бит и ключ K (англ. key — ключ) размером k бит и на выходе отдает блок шифротекста C (англ. cipher — шифр) размером n бит:

{\displaystyle E_{K}(M):=E(K,M):\{0,1\}^{k}\times \{0,1\}^{n}\to \{0,1\}^{n}.}

Большинство блочных шифров являются итеративными. Это означает, что данный шифр преобразует блоки открытого текста (англ. plaintext) постоянной длины в блоки шифротекста (англ. ciphertext) той же длины посредством циклически повторяющихся обратимых функций, известных как раундовые функции.^[10] Это связано с простотой и скоростью исполнения как программных, так и аппаратных реализаций. Обычно раундовые функции используют различные ключи, полученные из первоначального ключа:

{\displaystyle C_{i}=R_{K_{i}}(C_{i-1})}

,

где C_i — значение блока после i-го раунда, C₀ = M — открытый текст, K_i — ключ, используемый в i-м раунде и полученный из первоначального ключа K.
Пото́чный^[1][2] или Пото́ковый шифр^[3] — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному’?????????????&
^6+9*874ольшинство существующих шифров с секретным ключом однозначно могут быть отнесены либо к поточным, либо к блочным шифрам. Но теоретическая граница между ними является довольно размытой. Например, используются алгоритмы блочного шифрования в режиме поточного шифрования (пример: для алгоритма DES режимы CFB и OFB).

26. КРИПТОГРАФИЧЕСКИЕ ХЕШ-ФУНКЦИИ, ИХ СВОЙСТВА И ИСПОЛЬЗОВАНИЕ В КРИПТОГРАФИИ.
Хеш-функция (англ. hash function от hash — «превращать в фарш», «мешанина»^[1]), или функция свёртки — функция, осуществляющая преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины, выполняемое определённым алгоритмом. Преобразование, производимое хеш-функцией, называется хешированием. Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования называется «хешем», «хеш-кодом».

К криптографическим хеш-функциям предъявляются следующие требования:

1. Сопротивление поиску первого прообраза: при наличии хеша {\displaystyle h}

должно быть трудно найти какое-либо сообщение {\displaystyle m}

, такое что {\displaystyle h=hash(m)}

, Это свойство связано с понятием односторонней функции. Функции, у которых отсутствует это свойство, уязвимы для атак нахождения первого прообраза.

2. Сопротивление поиску второго прообраза: при наличии сообщения {\displaystyle m_{1}}

, должно быть трудно найти другое сообщение {\displaystyle m_{2}}

(не равное {\displaystyle m_{1}}

) такое, что {\displaystyle hash(m_{1})=hash(m_{2})}

. Это свойство иногда называют слабым сопротивлением поиску коллизий. Функции, у которых отсутствует это свойство, уязвимы для атак поиска второго прообраза.

3. Стойкость к коллизиям

Коллизией для хеш-функции называется такая пара значений {\displaystyle m}

и {\displaystyle m}

′, {\displaystyle m\neq m}

′, для которой {\displaystyle H(m)=H(m')}

. Так как количество возможных открытых текстов больше числа возможных значений свёртки, то для некоторой свёртки найдётся много прообразов, а следовательно, коллизии для хеш-функций обязательно существуют. Например, пусть длина хеш-прообраза 6 битов, длина свёртки 4 бита. Тогда число различных свёрток — {\displaystyle 2^{4}=16}

, а число хеш-прообразов — {\displaystyle 2^{6}=64}

, то есть в 4 раза больше, значит хотя бы одна свёртка из всех соответствует 4 прообразам.

4. Псевдослучайность: должно быть трудно отличить генератор псевдослучайных чисел на основе хеш-функции от генератора случайных чисел, например, он проходит обычные тесты на случайность.

Идеальной криптографической хеш-функцияей является такая криптографическая хеш-функция, к которой можно отнести пять основных свойств:

Детерминированность. При одинаковых входных данных результат выполнения хеш-функции будет одинаковым (одно и то же сообщение всегда приводит к одному и тому же хешу);
Высокая скорость вычисления значения хеш-функции для любого заданного сообщения;
Невозможность сгенерировать сообщение из его хеш-значения, за исключением попыток создания всех возможных сообщений;
Наличие лавинного эффекта. Небольшое изменение в сообщениях должно изменить хеш-значения, так широко, что новые хеш-значения не совпадают со старыми хеш-значениями;
Невозможность найти два разных сообщения с одинаковыми хеш-значениями.

На сегодняшний день подавляющую долю применений хеш-функций «берут на себя» алгоритмы MD5, SHA-1, SHA-256, а в России — ещё и ГОСТ Р 34.11-2012 (Стрибог).

SHA-256

Отдельно выделяется алгоритм SHA-256, который применяется в алгоритмах хеширования биткойна и других криптовалют. Как понятно из названия криптографической хеш-функции, выходной хеш составляет в длину 256 бит, соответствующую энтропию можно определить как множество значений от 1 до 2 в степени 256 — огромное число значений, что делает взлом и расшифровку крайне трудоёмким процессом, опирающимся на последовательный перебор.

Применение криптографических хеш-функций: ЭЦП, проверка парольной фразы, биткойн.

27. МЕТОДЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ, ИХ ИСПОЛЬЗОВАНИЕ В КРИПТОГРАФИИ.
Большое значение для криптографии имеет генерация истинно случайных (непредсказуемых) чисел. Случайные числа используются при генерации сеасовых ключей (а также открытых и закрытых ключей асимметричных алгоритмов), во многих криптографических протоколах. Многие приложения имеют уязвимости связанные именно с предсказуемостью генерируемых паролей, сеансовых ключей и т.д.
Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях.
Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди
Емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.
Генераторы псевдослучайных чисел стандартных библиотек ЯП по «зерну».

К ним предъявляются следующие требования:

Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.
Портируемость алгоритма на различные системы.
Скорость получения последовательности. Чем быстрее, тем лучше.
Повторяемость результата.

Линейный конгруэнтный генератор (LCG)

Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом.

const long randMax = 4294967296;

state = 214013 * state + 2531011;

state ^= state >> 15;

return (uint) (state % randMax);

XorShift

Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.

state ^= state << 13;

state ^= state >> 17;

state ^= state << 5;

return state;

Вихрь Мерсенна

Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно.

Перемешанный конгруэнтный генератор (PCG)

Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.
Одни из самых популярных хеш-функций — это MurMur3 и WangHash.

Наиболее распространены линейный конгруэнтный метод, метод Фибоначчи с запаздываниями, регистр сдвига с линейной обратной связью, регистр сдвига с обобщённой обратной связью.

Комбинированные подходы

Комбинированные подходы бывают двух типов:

Сочетание хеш-функции и генератора случайных чисел.
Иерархические генераторы.

Так как такие генераторы чаще всего применяются для генерации уникальных симметричных и асимметричных ключей для шифрования, они чаще всего строятся из комбинации криптостойкого ГПСЧ и внешнего источника энтропии (и именно такую комбинацию теперь и принято понимать под ГСЧ).
Почти все крупные производители микрочипов поставляют аппаратные ГСЧ с различными источниками энтропии, используя различные методы для их очистки от неизбежной предсказуемости.
В персональных компьютерах авторы программных ГСЧ используют гораздо более быстрые источники энтропии, такие, как шум звуковой карты или счётчик тактов процессора. Сбор энтропии являлся наиболее уязвимым местом ГСЧ. Эта проблема до сих пор полностью не разрешена во многих устройствах (например, смарт-картах), которые таким образом остаются уязвимыми, текущее время в миллисекундах, свободное количество памяти, размер жесткого диска, шумы токов.
Для ряда криптографических преобразований используют случайные первичные состояния либо целые последовательности.
Последовательность называется криптографически надежной псевдослучайной последовательностью, если вычислительно неосуществимо предсказать следующий бит, имея полное знание алгоритма и аппаратуры и всех предшествующих битов потока.

28. СИСТЕМЫ ШИФРОВАНИЯ С ОТКРЫТЫМИ КЛЮЧАМИ. КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ.
Криптографическая система с открытым ключом (разновидность асимметричного шифрования, асимметричного шифра) — система шифрования и/или электронной подписи (ЭП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для проверки ЭП и для шифрования сообщения. Для генерации ЭП и для расшифровки сообщения используется закрытый ключ^[1]. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.
Асимметричное шифрование с открытым ключом базируется на следующих принципах:

Можно сгенерировать пару очень больших чисел (открытый ключ и закрытый ключ) так, чтобы, зная открытый ключ, нельзя было вычислить закрытый ключ за разумный срок. При этом механизм генерации является общеизвестным.
Имеются надёжные методы шифрования, позволяющие зашифровать сообщение открытым ключом так, чтобы расшифровать его можно было только закрытым ключом. Механизм шифрования является общеизвестным.
Владелец двух ключей никому не сообщает закрытый ключ, но передает открытый ключ контрагентам или делает его общеизвестным.

Если необходимо передать зашифрованное сообщение владельцу ключей, то отправитель должен получить открытый ключ. Отправитель шифрует свое сообщение открытым ключом получателя и передает его получателю (владельцу ключей) по открытым каналам. При этом расшифровать сообщение не может никто, кроме владельца закрытого ключа.

В результате можно обеспечить надёжное шифрование сообщений, сохраняя ключ расшифровки секретным для всех - даже для отправителей сообщений.

Этот принцип можно объяснить через бытовую аналогию «замо́к — ключ от замка́» для отправки посылки. У участника A есть личный замок и ключ от него. Если участник А хочет получить секретную посылку от участника Б, то он публично передаёт ему свой замок. Участник Б защёлкивает замок на секретной посылке и отправляет её участнику А. Получив посылку, участник А открывает ключом замок и получает посылку.

Знание о передаче замка и перехват посылки ничего не дадут потенциальному злоумышленнику: ключ от замка есть только у участника А, поэтому посылка не может быть вскрыта.
Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций {\displaystyle f(x)}

, что по известному {\displaystyle x}

довольно просто найти значение {\displaystyle f(x)}

, тогда как определение {\displaystyle x}

из {\displaystyle f(x)}

невозможно за разумный срок.
Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркла о распространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи — Хеллмана,

1 2 3