Сапаргалиев Е. МТ11(3) КР. Сызыты тдб немесе арж кірісіне гармоникалы сер берген кезде
 Скачать 374.05 Kb. Скачать 374.05 Kb.
|
|
Сызықтық ТДБ немесе АРЖ кірісіне гармоникалық әсер берген кезде: ауыспалы процесс біткен кезде, шығыс сипаттаманың да түрі периодтық функция болады: АРЖ еріксіз тербеліс режимінде болады [1]. W(j)өрнегін нақты P() және жорамал Q() бөліктеріне бөлуге болады: мұнда: P(), Q(), A(), () - бойынша полиномдар. кесте. ТДБ-дың динамикалық параметрлерінің мәндері
Сонымен, жиілік өзгерген кезде P,Q, A, шамалары да өзгереді. Сондықтан осы шамалар үшін де жиіліктік сипаттамаларды құруға болады. Осыған сәйкес: P() – нақты жиіліктік сипаттама (НЖС); Q() – жорамал жиіліктік сипаттама (ЖЖС); Aж () – амплитудалық жиіліктік сипаттама (АЖС); ж () – фазалық жиіліктік сипаттама (ФЖС). Сипаттамалар арасындағы қатынас төмендегідей өрнектермен анықталады: 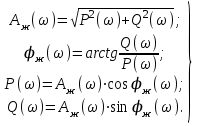 (6) (6)Онда: Бұл өрнектен аламыз: (6) өрнегін пайдалана отырып, аламыз: 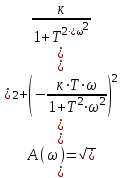 - АЖС; - АЖС;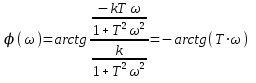 - ФЖС. - ФЖС. 2-кесте Инерциялы буынның жиіліктік сипаттамаларының есептелген мәндері
Инерциалы буынның жиіліктік сипаттамалыарының графиктері 1, 2, 3, 4 – суреттерде көрсетілген. Инерциалы буынның АФЖС – ын P() және Q() мәндері бойынша декарт координатында (5 – сурет) A() және () мәндері бойынша поляр координатында құруға болады. 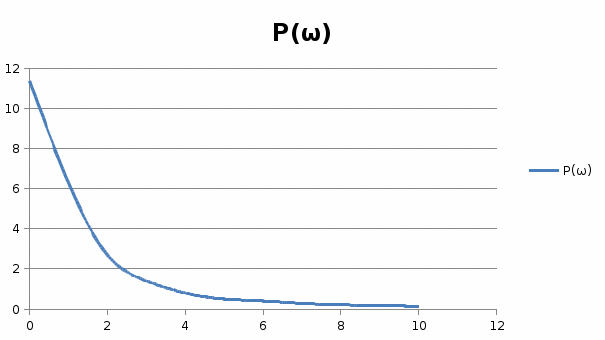 1 – сурет. Нақты жиіліктік сипаттама 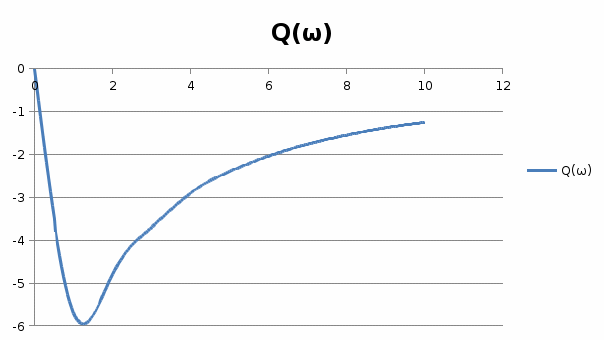 2 – сурет. Жорамал жиіліктік сипаттама 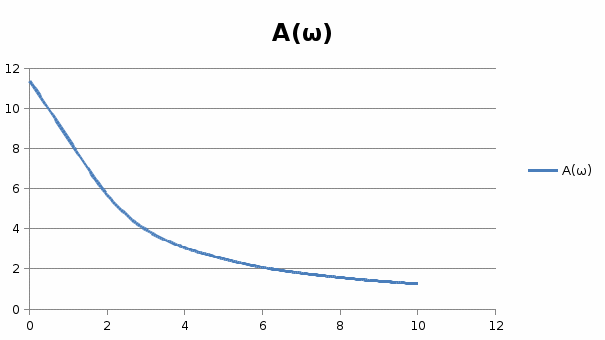 3 – сурет. Амплитудалық жиіліктік сипаттама 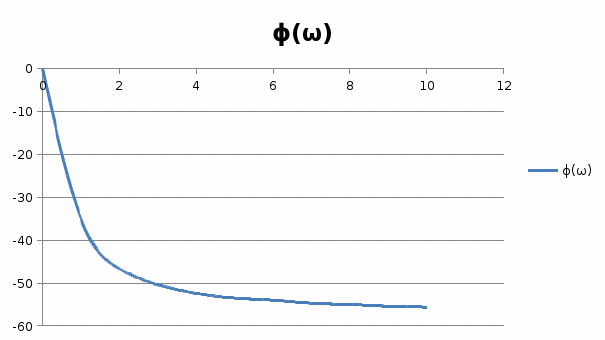 4 – сурет. Фазалық жиіліктік сипаттама 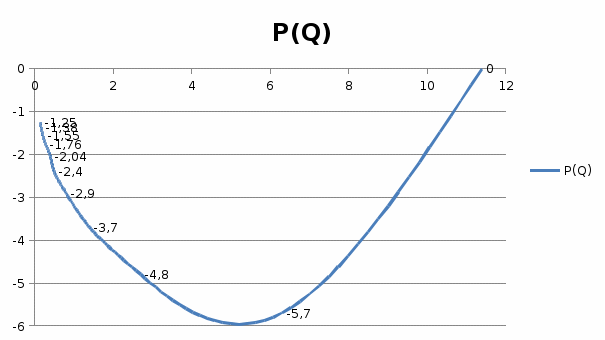 5 – сурет. Декарт координатында салынған амплитуда – фазалық жиіліктік сипаттама Басқада ТДБ – дың ЖС – лары жоғарыда берілген әдістеме бойынша құрылады. Бұл тақырыпты баянды ету үшін студенттер ӨЖ – 1 орындайды [2]. 2.Жүйенің жиіліктік сипаттамаларын есептеу және құру Берілген нұсқа үшін сандық мағынаны есептеу арқылы: 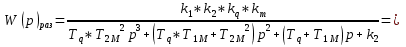 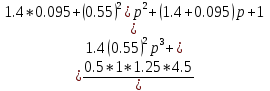 p=jωқоямыз, өзгерте отырып мынаны аламыз: Бөлгішке байланысты алымы мен бөлімін кешенді санға көбейтеміз және бөлеміз: Бұдан алатынымыз: 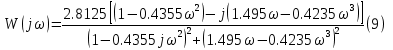
3-кесте. Есептеудің қорытындысы 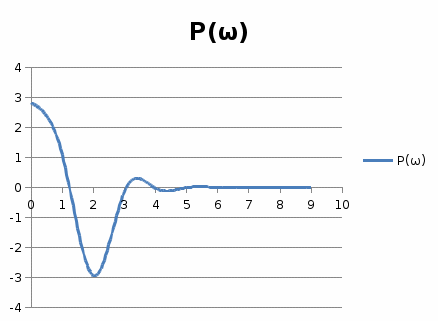 6 – сурет. Нақты жиіліктік сипаттама 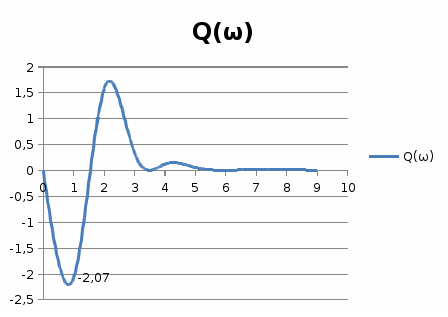 7-сурет Жорамал жиіліктік сипаттама 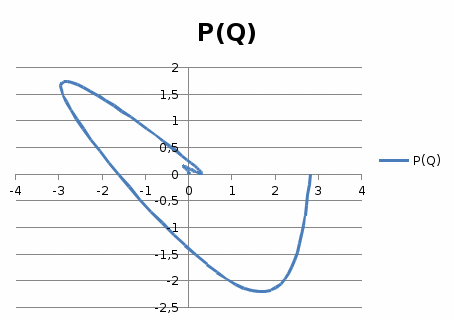 8-сурет Декарт координатында салынған амплитуда – фазалық жиіліктік сипаттама Жүйенің тұрақтылығын Гурвиц және Михайлов өлшемі бойынша анықтау үшін тұйық ортаға арналған сипаттамалы теңдеуді табу қажет. Алшақ тұрған жүйе үшін алдын-ала тапсыру функциясы алынды. Теріс кері байланысқан тұйықталған АС үшін тапсыру функциясы тең болады: 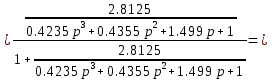 мұндағы бөлгіш АС тұйықталған жүйесі үшін сипаттамалы есептеу болып табылады, яғни 2.1 Михайлов өлшемі бойынша тұрақтылықты анықтаймыз Тұйықталған АЖ сипаттамалы есептеуіне р операторының орнына jωмәнін қоямыз: ωЄ(0,∞) шегінде ω әртүрлі мәнін бере отырып, берудің комплексті коэффициентінің годограф нүктесінің R(ω) , J(ω) координатасын табамыз. 4-кесте Михайлов критерийсі бойынша есептеудің қорытындысы
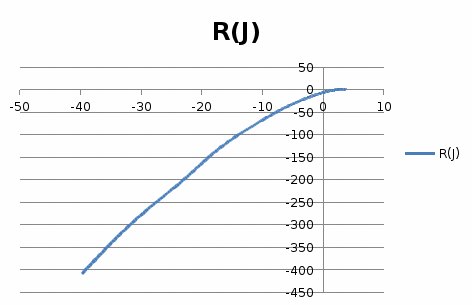 9-сурет Михайлов критерийсі бойынша сұлба Тұрақтылық шарттың математикалық түрде жазылуы дегеніміз – ауыспалы процестің басынан, уақыт шексіздікке ұмтылған кезде, мұнда  123n 123n0 . . . . . . . . . . 0 0 . . . . . . . . . . . Кесте құрудың ережесі келесі: - бас диагональ бойынша 1 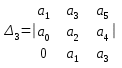 ; …… ; ……Тұрақтылықтың Гурвиц критерийі бойынша барлық Бұл шарт – жеткілікті шарт та болады. Одан жоғары ретті жүйе үшін, сипаттамалық теңдеудің барлық коэффициенттері оң болуы шарты орындалуынан басқа, келесі теңсіздіктер орындалу қажетті және жеткілікті болады: үшінші ретті жүйе үшін: төртінші ретті жүйе үшін: бесінші ретті жүйе үшін: 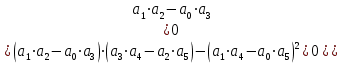 (19) (19)алтыншы ретті жүйе үшін: 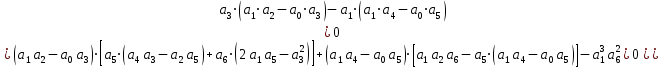 (20) (20)Гурвиц критерийі бойынша АРЖ тұрақтылығын бағалаңыз егер, оның сипаттамалық теңдеуі келесі түрге ие : 0,4235 Үшінші ретті теңдеу үшін, Гурвиц критерийі бойынша, тұрақтылықтың шарты болып теңдеу коэффициенттерінің оң болуы ғана емес: сонымен қатар, теңсіздік орындалу қажет: Сонымен, жүйе тұрақсыз. 2.3 Вышнеградский критерийсі бойынша тұрақтылықты анықтаймыз. Сипаттамалы есептеу үшінші тәртіпке ие бұл критерий жүйенің тұрақтылығын анықтау кезінде қолданылады. Біздің жүйеде үшінші тәртіптегі сипаттамалы есептеу Есепті р3 бірге тең болатындай етіп өзгерту керек. Бұл үшін сипаттамалы есептеудің барлық мүшелерін 0,5915-ке бөлеміз және бұдан шығатыны: мұндағы Осы берілген мән бойынша Х және У табамыз. Х-тің формуласы: У-тіңформуласы: 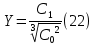 Берілген мәндерді орнына қоямыз: Бұдан алатынымыз: Яғни ХУ 3.Тербеліс буынын табу ТДБ-дың динамикалық параметрлерінің мәндерінің ішінен тербеліс буынының формуласын жазамыз: W (p)= 1-кесте бойынша мәндерді алып, берілген (23) формулага қоямыз. Бұдан шығатыны: Мұндағы ал, тең. 5-кесте Тербеліс буыны бойынша есептеудің қорытындысы
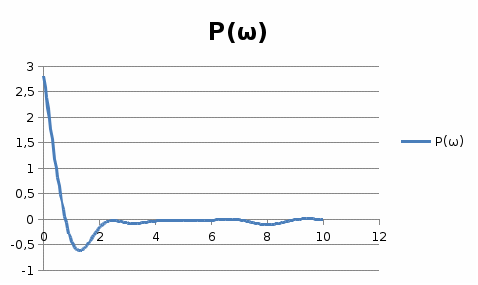 10-суретНақты жиіліктік сипаттама 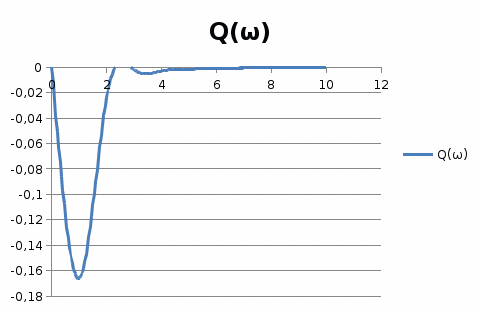 11-сурет Жорамал жиіліктік сипаттама 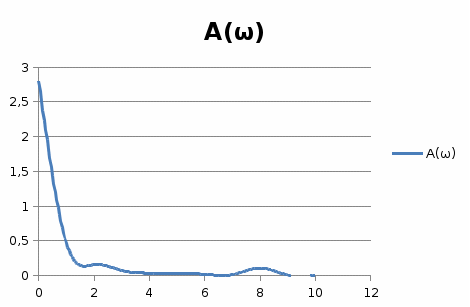 12-сурет Амплитудалық жиіліктік сипаттама 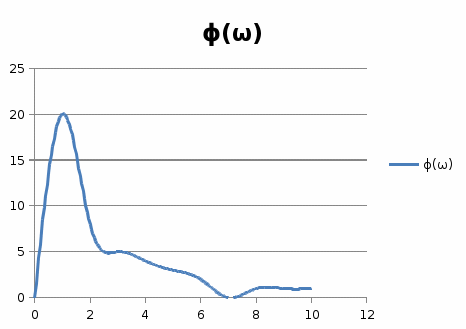 13-сурет Фазалық жиіліктік сипаттама 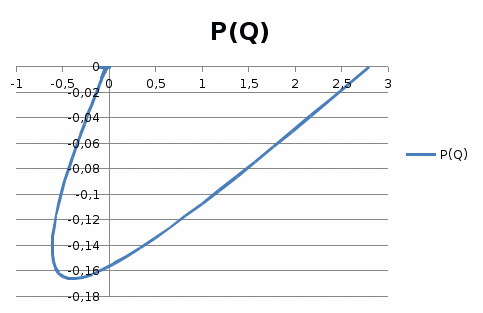 14-сурет Декарт координатында салынған амплитуда – фазалық жиіліктік сипаттама 4. Автоматты реттеу жүйесінің жиіліктік сипаттамаларын есептеу мен құру АРЖ-ның динамикалық параметрлері мен құрылымдық сұлбасы 6,7 - кестелерде көрсетілген. АРЖ - нің жиіліктік сипаттамаларын құру үшін 1.1- бөлімдегі кезеңдерді орындау қажет. Тек бұл жерде жүйеге тиісті кезеңдерді орындап, тапсырмада талап етілген сипаттамаларды алу керек 6-кесте. АРЖ-ның құрылымдық сұлбалары 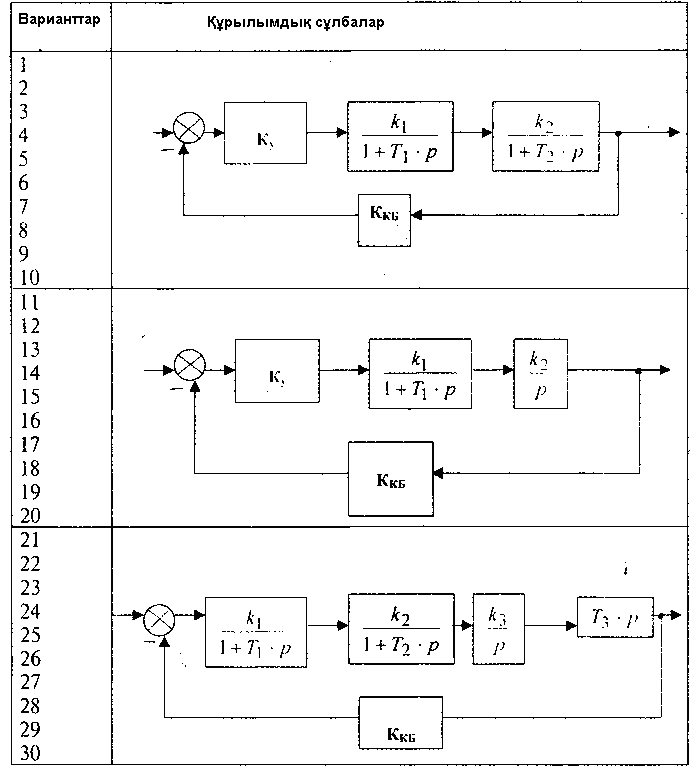 7-кесте. АРЖ-ның динамикалық параметрлерінің мәндері
2-нұсқаның мәнін қойып, құрылымдық сұлба бойынша есепті шығарамыз. 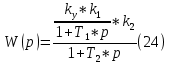 Берілген мәндерді формулаға қоямыз, бұдан ал, W(p)=jωқоямыз, бұдан шығатыны яғни Р(ω) және Q(ω) мынаған тең 8-кесте Автоматты реттеу жүйесінің жиіліктік сипаттамаларының нәтижесі
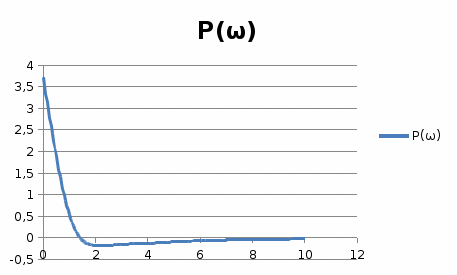 15 – суретНақты жиіліктік сипаттама 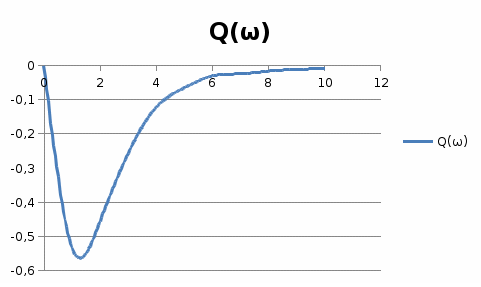 16-сурет Жорамал жиіліктік сипаттама 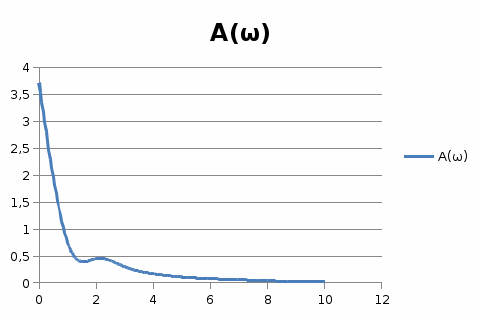 17-сурет Амплитудалық жиіліктік сипаттама 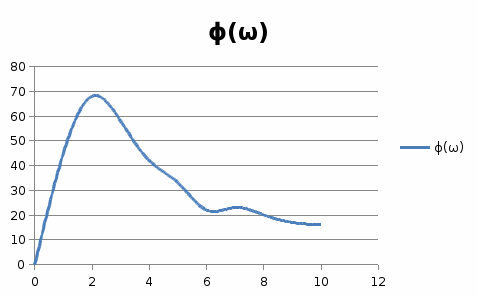 18-сурет Фазалық жиіліктік сипаттама 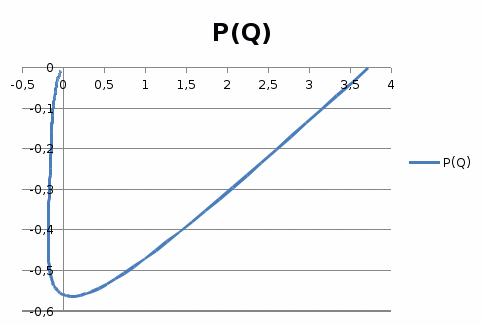 19-сурет Декарт координатында салынған амплитуда – фазалық жиіліктік сипаттама | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
