Скалярное произведение векторов (без доказательства). Скалярное произведение векторов. Определение
 Скачать 97.53 Kb. Скачать 97.53 Kb.
|
|
Скалярное произведение векторов. Определение. Скалярным произведением двух ненулевых векторов 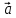 и и 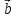 называется число, равное произведению длин этих векторов и косинуса угла между ними, называется число, равное произведению длин этих векторов и косинуса угла между ними, т.е. | 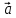 | |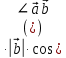 . .Скалярным произведение нулевого вектора на любой вектор называется число нуль. Обозначения: ( 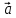 , , 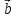 ) или ) или 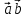 или или 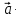 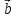 или или 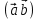 . .Свойства скалярного произведения. Длина любого вектора равна корню квадратному из скалярного произведения данного вектора на себя, | 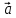 | |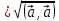 . Доказательство самостоятельно. . Доказательство самостоятельно.Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда их скалярное произведение равно нулю. Доказательство в одну сторону ( 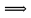 ) ) Доказательство в другую сторону ( 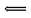 ) ) Доказано. Коммутативность: для любых векторов 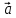 и и 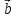 выполняется ( выполняется (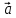 , , 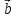 ) = ( ) = (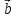 , , 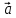 ) )Доказательство самостоятельно. В декартовой системе координат скалярное произведение векторов вычисляется по формуле: ( 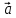 , , 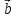 ) = ) = 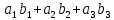 , где , где 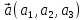 и и 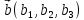 . .Доказательство … Для любых векторов 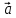 , , 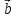 и произвольного числа α выполнено: и произвольного числа α выполнено: (α 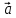 , , 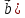 = α( = α(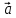 , , 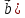 Доказательство… Для любых векторов 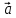 , , 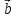 , , 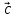 выполнено: выполнено: 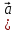 + + 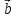 , , 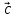 ) = ) = 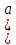 , , 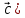 + ( + (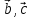 ) ) |
