Подготовка к лр 7н. Скатывание тела с наклонной плоскости
 Скачать 28.66 Kb. Скачать 28.66 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ИВТ отчет по лабораторной работе №1 по дисциплине «Механика» Тема: Скатывание тела с наклонной плоскости Выполнил: Группа № Преподаватель:
Цель работы. Проверить выполнимость основного уравнения динамики вращательного движения (уравнения моментов) и закона сохранения механической энергии в опыте по скатыванию круглых тел с наклонной плоскости. Приборы и принадлежности. Установка, представляющая собой наклонную плоскость(1); винт (2), при помощи которого можно менять угол плоскости α к горзионту; шкала, которая изменяет угол α (3); полый и сплошной цилиндры разных масс (4); электромагнит (5) для удержания цилиндра в верхней части плоскости; секундомер СЭ-1 (при нажатии на СЭ-1 кнопки «Пуск» магнит отключается и включается секундомер, а при нажатии кнопки «Стоп» магнит включается); линейка (6), с помощью которой измеряется пройденное цилиндром расстояние, закреплённая вдоль плоскости; датчик (7), закреплённый вдоль плоскости, который выключает секундомер в момент касания цилиндром финишной точки; тумблер «плоскость/удар» для регулирования режима работы установки ОСНОВНЫЕ РАСЧЁТНЫЕ ФОРМУЛЫ. Основной закон динамики вращательного движения (уравнение моментов. 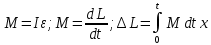 где 𝑀=∑𝑀𝑖 — результирующий момент всех внешних сил, действующих на него; L — момент импульса тела; I — момент инерции тела. Момент импульса тела. 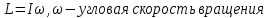 Моменты силы и импульса определяться как скалярные произведения M=r*F и L=r*p, где r — положение точки приложения силы F и импульса тела p относительно произвольной точки O. Момент инерции цилиндра относительно его центра масс. 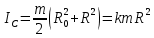 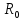 – радиус сплошного цилиндра, R – радиус полого, k=[1+(𝑅0/𝑅)2]/2 — коэффициент инерции тела. Для тонкостенного цилиндра – радиус сплошного цилиндра, R – радиус полого, k=[1+(𝑅0/𝑅)2]/2 — коэффициент инерции тела. Для тонкостенного цилиндра 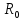 =0 и k=1/2. =0 и k=1/2.Теорема Штейнера. 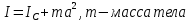 Если другая ось вращения тела параллельна оси, проходящей через центр массы тела, и смещена от неё на расстояние α, то момент инерции тела относительно новой оси рассчитывается по теореме Штейнера. Если тело катится по поверхности, то момент инерции относительно точки О касания тела и поверхности по теореме Штейнера равен (𝛼=𝑅): 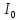 = =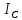 +𝑚 +𝑚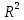 =(𝑘+1)𝑚 =(𝑘+1)𝑚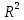 . .Момент силы тяжести 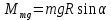 Ускорение скатывания тела 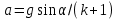 Считаем, что в точке О касания тела и плоскости нет проскальзывания, тогда мгновенная скорость в этой точки в любой момент времени равна 0. Ось вращения, проходящая через эту точку, будет называться мгновенной осью вращения. Для описания тела возьмём точку полюс в точке О, через которую проходит ось мгновенного вращения. Относительно этой точки силы N и Fтр равны 0, а момент силы тяжести равен 𝑀𝑚𝑔=𝑚𝑔𝑅sin𝛼. Момент инерции круглого тела относительно оси О равен 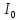 =(𝑘+1)𝑚 =(𝑘+1)𝑚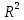 , угловое ускорение вращения тела 𝜀=𝛼/𝑅. Уравнение вращательного движения тела относительно оси, проходящей через точку О, 𝑀𝑚𝑔= , угловое ускорение вращения тела 𝜀=𝛼/𝑅. Уравнение вращательного движения тела относительно оси, проходящей через точку О, 𝑀𝑚𝑔=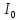 𝜀, примет вид 𝑚𝑔𝑅sin𝛼=(𝑘+1)𝑚 𝜀, примет вид 𝑚𝑔𝑅sin𝛼=(𝑘+1)𝑚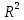 𝛼/𝑅 𝛼/𝑅Сила трения сцепления 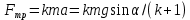 Если выбрать полюс в С(ЦМ тела), то моменты сил N и mg будут равны 0, момент силы трения сцепления будет равен 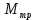 = =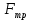 R. Момент инерции тела относительно оси С R. Момент инерции тела относительно оси С 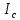 =𝑘𝑚 =𝑘𝑚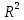 , а угловое ускорение 𝜀=𝛼/𝑅. Тогда уравнение вращательного движение , а угловое ускорение 𝜀=𝛼/𝑅. Тогда уравнение вращательного движение 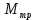 = =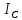 ε примет вид ε примет вид 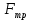 R=km R=km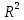 α/R. α/R.Найденная сила трения сцепления аналогична силе трения покоя. 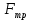 max = µN. N = µmgcosα => max = µN. N = µmgcosα => 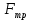 = kmgsinαk+1 ≤ µmgcosα = = kmgsinαk+1 ≤ µmgcosα = 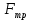 max. => µ≥ktgα/(k+1) max. => µ≥ktgα/(k+1)Кинетическая энергия 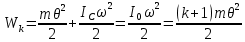 Для описания скатывания тела можно использовать энергетический метод. Скорость тела, скатившегося с высоты h, в основание наклонной плоскости 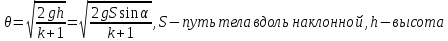 Работа силы нормальной реакции опоры равна N, а так же работа силы трения сцепления равны 0, следовательно 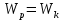 Время скатывания тела 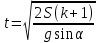 Если параметрам полого и сплошного цилиндра присвоить индексы 1 и 2 соответственно, а отношение отрезков как n= 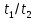 , то учитывая, что они прошли одинаковый путь, получим отношения их ускорений и скоростей , то учитывая, что они прошли одинаковый путь, получим отношения их ускорений и скоростей 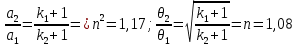 Эти соотношения также можно использовать для экспериментальной проверки правильности основного уравнения динамики вращательного движения. ПРОТОКОЛ НАБЛЮДЕНИЙ ЛАБОРАТОРНАЯ РАБОТА №7Н СКАТЫВАНИЕ ТЕЛА С НАКЛОННОЙ ПЛОСКОСТИ Таблица 1. Измерение
Выполнил Факультет Группа № “ ”_____________ ____ Преподаватель Вопросы к лабораторной работе№1 (Вар. 7н) по теме «СКАТЫВАНИЕ ТЕЛА С НАКЛОННОЙ ПЛОСКОСТИ» 13) Приведите три формы основного уравнения динамики вращательного движения. Как называются параметры, входящие в него? 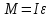 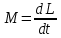 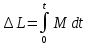 M — результирующий момент всех внешних сил, действующих на него L – момент импульса тела I – момент инерции тела ε – угловое ускорение t – время вращения 15) Как вычисляется кинетическая энергия тела, совершающего сложное поступательно-вращательное движение? Если тело одновременно участвует в поступательном и вращательном движениях, то его полная энергия определится по формуле: 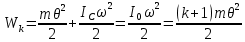 m – масса тела υ – линейная скорость 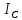 - известный момент инерции относительно оси, проходящей через центр масс тела - известный момент инерции относительно оси, проходящей через центр масс тела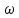 – угловая скорость – угловая скорость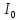 - момент инерции относительно точки О касания тела и поверхности - момент инерции относительно точки О касания тела и поверхности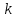 – коэффициент инерции тела – коэффициент инерции тела | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
