Сообщение. Сообщение к презентации. Слай в iii в
 Скачать 154.55 Kb. Скачать 154.55 Kb.
|
|
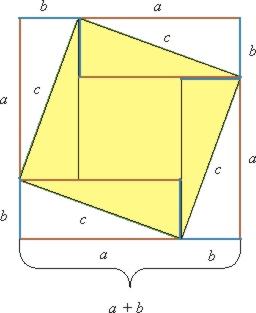
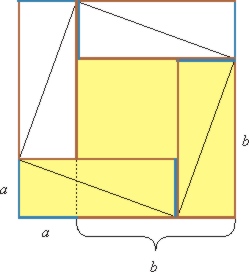
Слайд2. В III в. до н.э. Цинь Шихуанди, первый император династии Цинь, образовал единое государство. В годы его правления началось строительство Великой Китайской стены. Цинь предпринял меры по политическому и административному объединению страны: унифицировал единицы измерения, ввел единую денежную единицу, распространял единообразное письмо. В истории он известен циньским погромом: в 213 г. этот император приказал сжечь все классические книги, по‑видимому, для того, чтобы ликвидировать прежние традиции. Слайд3. Однако вскоре в династии Хань (II в. до н.э.‑II в. н.э.) древние книги начали восстанавливать. Ко II в. до н.э. относится изобретение бумаги (хотя традиционной датой изобретения бумаги из растительных волокон считается 105 г. н.э.), кисти для письма и рисования. Тогда же впервые в Китае начали проводить официальные экзамены при наборе государственных чиновников. Таким образом, математическому образованию уделялось серьезное внимание. В это же время были созданы наиболее древние из дошедших до нас сочинений — «Трактат об измерительном шесте» и самая известная книга — «Математика в девяти книгах» (окончательную редакцию которой сделал Чжан Цан во II в. до н.э.). Она была предназначена для чиновников, торговцев, землемеров, строителей. В ней помещено 246 задач с указаниями для их решения. Слайд4. Согласно китайскому «Трактату об измерительном шесте» (II в. до н. э.), теорема Пифагора для частного случая – треугольника со сторонами 3, 4, 5 – была известна в Китае еще в XII в. до н. э., а в общем случае – в VI в. до н. э. В комментариях к этой книге указывается, что доказательство теоремы основывалось на следующем чертеже:
На этом чертеже видно, что большой квадрат (a + b)2 больше, чем квадрат гипотенузы c2, на четыре прямоугольных треугольника c катетами a и b, т. е. на 2ab: (a + b)2 = c2 + 2ab. Значит, квадрат гипотенузы равен большому квадрату, уменьшенному на два прямоугольника со сторонами a и b, то есть закрашенной фигуре. А эта фигура, в свою очередь, равна сумме квадратов со сторонами a и b:
На том же чертеже можно увидеть и другое доказательство. Квадрат гипотенузы больше, чем маленький квадрат в центре (a – b)2, на те же четыре треугольника, или на два прямоугольника: c2 = (a – b)2 + 2ab Это нас снова приводит к той же закрашенной фигуре, равной сумме квадратов катетов Слайд5. Книга 1 “Измерение полей” – посвящена арифметике дробей и вычислению площадей различных плоских фигур. Книга 2 “Соотношение между различными видами зерновых культур” – посвящена решению задач на пропорции. В книге 3 “Деление по ступеням” – содержатся задачи на деление пропорционально данным числам. 4 книга “Шао Гуан” – посвящена нахождению стороны прямоугольника и квадрата по его площади, ребра куба по объему, а также определению диаметров круга и сферы. В книге 5 “Оценка работ” – измеряются объемы стен, рвов, каналов, плотин различной формы и определяется количество рабочих, необходимых для выполнения работ. В книге 6 “Пропорциональное распределение” – решается задача справедливого распределения налогов и поставок между уездами в зависимости от различных условий. В книге 7 “Избыток и недостаток” – решаются системы двух линейных уравнений с двумя неизвестными методом ложного положения. В восьмой книге “Фан Чэн” – решаются системы n линейных уравнений с n неизвестными. В девятой книге “Гоу-гу” решаются задачи на теорему Пифагора. Книги имеют различный математический уровень: они явно были написаны в разное время. Они являются итогом математических достижений Китая до начала нашей эры. В VII‑X вв. н.э., неоднократно дополненный и подвергшийся переработке, он сделался основным учебником для чиновников. Слайл6. Китайские иероглифические цифры возникли во II тысячелетии до н.э. и установились к III в. до н.э. Эти иероглифы применяются и в настоящее время. Система счисления — десятичная. В научных записях числа изображались различно расположенными, горизонтальными и вертикальными, палочками и кружочком. Арифметические действия производились на счетной доске с помощью палочек. Слайд7. При этом приходилось иногда вычитать из меньшего числа большее. Здесь впервые в истории математики появились отрицательные числа. Они выделялись на счетной доске палочками другого цвета или другой формы, а при письме записывались чернилами другого цвета. Позже их назвали «фу» и стали толковать как «долг», в отличие от положительных чисел «чжэн» («имущество»). Слайд8. В древних текстах дробь записывали по схеме « n-ых m». Сначала выполняется деление основной единицы на n частей, а затем берётся m таковых. Слайд9. Девятая книга «Математики в девяти книгах» была посвящена геометрическим задачам. При решении некоторых из них применялась теорема Пифагора. Вычислялись площади многоугольников, круга и его частей, кругового кольца, объемы прямоугольного параллелепипеда, прямой призмы, пирамиды с квадратным основанием. В Китае теорема Пифагора называлась правилом «гоу-гу»: термины «гоу» (исходно «крюк») и «гу» («ребро», «связка») обозначали горизонтальный (обычно меньший) и вертикальный (обычно больший) катеты. В классическом китайском трактате «Математика в девяти книгах» (II в. до н. э.) последняя книга называется «Гоу-гу» и посвящена задачам, решаемым с помощью теоремы Пифагора. Вот пример такой задачи. Слайд10. Имеется водоем со стороной в 1 чжан (10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?  Рис. 3. Задача о камыше, Китай, II в. до н. э. В самом трактате «Математика в девяти книгах» решение не дается, приводится только правило, по которому можно вычислить ответ, причем в общем виде: «Половину стороны водоема умножь самое на себя, надводную часть в 1 чи умножь самое на себя, вычти это из первого, остаток раздели на удвоенную надводную часть камыша, получишь глубину воды. Прибавь количество чи надводной части, получишь длину камыша». То есть, в алгебраических обозначениях, если сторона водоема равна 2a (10 чи), а надводная часть b (1 чи), то глубина водоема равна (a2 – b2) / 2b, а длина камыша (((a2 – b2) / 2b) + b) Слайд11. Пусть глубина водоема x чи. Тогда длина камыша (x + b) чи. По теореме Пифагора квадрат этой длины равен сумме квадратов глубины водоема и расстояния от центра до берега, т. е. (x + b)2 = x2 + a2, откуда x2 + 2bx + b2 = x2 + a2, 2bx + b2 = a2, x = (a2 – b2) / 2b, в полном соответствии с ответом, данным в трактате «Математика в девяти книгах». При подстановке конкретных чисел (a = 5, b = 1) получаем x = (25 – 1) / 2 = 12 (чи), а длина камыша, соответственно, x + b = 13 (чи). Китайская математика не была изолирована от развития математики в других странах. Имеются некоторые факты взаимного влияния математики Китая, Индии, стран ислама. Например, появление отрицательных чисел в Индии, десятичных дробей в Средней Азии, близость китайской и индийской нумераций и др. Связи между математиками Китая и Индии прослеживаются с первых веков н.э. и особенно усиливаются в период распространения буддизма, когда в Китае появляются индийские ученые. Древняя Индия Слайд12. В истории Индии имеется достаточно фактов, свидетельствующих о наличии экономических и политических связей с греческими, арабскими государствами и с Китаем. Естественно, эти связи повлияли на развитие ее культуры. В истории математики тоже отмечается распространение математических знаний в обоих направлениях. Например, в V в. появилась переводная греческая астрономическая литература. Слайд13. В I тысячелетии до н.э. появились священные книги брахманов «Веды» («Знания»). К VII‑V вв. до н.э. относятся первые индийские письменные математические памятники. Большинство трактатов индийцев написаны на санскрите — языке религиозных книг. Этот давно вымерший язык объединял многочисленные народы Индии, говорившие на различных языках. Некоторые сведения о математике древней Индии содержатся в комментариях к «Ведам». Одной из таких книг была «Сульва сутра» («Правила веревки»), относящаяся к VI‑V вв. до н.э. В ней излагаются способы построения культовых сооружений и связанные с ними математические правила: построение прямого угла, квадрата, прямоугольника, деление отрезка пополам. Слайд14. Наиболее известными математиками были Ариабхата I (V в.), Брахмагупта (VII в.), Бхаскара I (VII в.), Бхаскара II (XII в.). Для их работ характерны арифметико‑алгебраические разделы и вопросы астрономии. Уже в IV в. появились астрономо‑математические труды — «сиддханты» («учения»). Важнейшая из сиддхант была написана Брахмагуптой 628 г. («Усовершенствованное учение Брахмы»), состояла она из 20 книг. Большая часть этого сочинения была посвящена астрономии, но две книги отводились арифметике, алгебре и геометрии. Бхаскара II написал трактат «Сиддханта‑широмани» («Венец учения») из четырех частей, посвященный астрономии и математике. Арифметическая часть этого труда — книга «Лилавати» («Прекрасная»), оставалась образцовым учебником в течение столетий. Она неоднократно переиздавалась, была переведена на многие языки. Отметим и такое своеобразие индийских трактатов: некоторые из них были написаны в стихах, чтобы математические правила можно было заучивать наизусть. Слайд15. Наиболее известным достижением индийской математики является наша современная десятичная позиционная система счисления. Установлено, что начиная с VI в. до н.э. в Индии была распространена десятичная непозиционная система счисления — числа «брахми». Каждая единица, десятка, сотня, тысяча имела свой символ. Эта система позже была вытеснена позиционной записью, заимствованной у вавилонян и переделанной на десятичную. Первое ее применение относится к источнику 595 г. Еще раньше был введен нуль, обозначаемый словом «сунья» («пустое»). Он изображался точкой, позднее знаком 0, возможно, от греческого слова «ouden» («ничто»). В отличие от вавилонян, нуль ставился и в конце числа. Отныне любое число стало записываться с помощью десяти знаков. Десятичная система счисления была заимствована арабами (VII‑VIII вв.) и начала свое продвижение на Запад. Слайд16.Дроби в Индии тоже известны очень давно. Индийцы записывали дроби так, как это делается в настоящее время: числитель над знаменателем, только без дробной черты. Правила действий над дробями почти не отличаются от современных. Слайд17. Начиная с Брахмагупты индийские математики пользовались отрицательными числами, трактуя их как долг, а положительные числа — как имущество. Брахмагупта приводит все правила арифметических действий над отрицательными числами. Например, сумма двух имуществ есть имущество, двух долгов — долг, имущества и долга — их разность и т.д. Слайд18. Выдающимся достижением индийских математиков было создание развитой алгебраической символики. Неизвестную величину они назвали “йаваттават”, что означало столько сколько, в дальнейшем использовался символ “йа”. Если неизвестных было несколько, то использовались названия цветов: калака (ка) – черный, нилака (ни) – голубой, питака (пи) – желтый, панду (па) – белый, лохита (ло) – красный. Иногда неизвестное обозначалось 0. Символ сложения “йу”, “гу” – умножение, “бха” – деление. Вычитание обозначалось точкой над вычитаемым или знаком ’+’ сзади. x 2 – ва, x 3 – гха, x 4 – ва-ва, x 5 – ва-гха и т.д. Знака = не было Слайд19. Знания индийских математиков в области геометрии уступают их арифметическим и алгебраическим знаниям. Геометрические факты приводились без доказательства. Чаще всего это был чертеж со словами “Смотри”. Такого рода доказательство теоремы Пифагора приводит Бхаскара в книге “Венец знаний”. Брахмагупта считал, что площадь четырехугольника можно вычислить по формуле что на самом деле верно только для четырехугольника, вписанного в окружность. Известны также некоторые формулы объемов тел: Слайд20. Уже древнейшая из синдхат “Сультасутра” – “Принципы измерения хорд” познакомила индийцев с тригонометрией хорд александрийских астрономов. Хорда – джива (тетива) впоследствии было заменено термином полухорда – ардха-джива (полутетива). Арабские переводчики записали это арабскими буквами – джайбл, что означало пазуха, впадина, последнее на латынь было переведено как синус. Пользовались индусы и линией косинуса – котиджива. Индусам были известны некоторые формулы тригонометрии: Индусы пользовались тенью, отбрасываемой шестом (гномоном), для определения высот и расстояний. Эти вычисления привели потом математиков стран ислама к тангенсам и котангенсам, которые они называли тенями. Индусских математиков интересовали задачи на суммирование рядов: сумма треугольных чисел, квадратов и кубов. Например, они использовали ряд  Индийские математики предвосхитили не только конечные результаты, но и методы, приводящие к ним. Так в современных учебниках по математическому анализу ряд arctan x получают с помощью способа, сходного с индийским. подинтегральная функция раскладывается в степенной ряд, затем почленно интегрируется. Таким образом, в Индии математика является очень древней наукой, составляющей часть старинной культуры. В ней тоже, как и в Китае, преобладали вычислительно‑алгоритмические методы и отсутствовали попытки построения дедуктивных систем. К какой династии относят создание «Математика в 9 книгах» Династия Тан Династия Хань+ Династия Цинь Династия Суй 2. Как называлась арифметическая часть труда Бхаскара II Биджаганита Ганитадхья Лилавати+ Голадхья 3. Какая из книг «Математика в 9 книгах» посвящена нахождению стороны прямоугольника и квадрата по его площади, ребра куба по объему, а также определению диаметров круга и сферы Измерение полей Шао Гуан+ Оценка работ Гоу-гу 4. Чему равна сумма имущества и долга согласно индийскому математику Брахмагупта Имуществу Долгу Их разности + Нулю Как выделялись отрицательные числа в Древнем Китае? Отрицательные числа выделялись на счетной доске палочками другого цвета или другой формы, а при письме записывались чернилами другого цвета. Отличительная особенность письма дроби в Древней Индии? Индийцы записывали дроби так, как мы это делаем сейчас: числитель писали над знаменателем, но черту дроби не писали. Как называется основной учебник для чиновников Древнего Китая? «Математика в 9 книгах» О чем говорится в книге «Сульва сутра» ? В ней излагаются способы построения культовых сооружений и связанные с ними математические правила: построение прямого угла, квадрата, прямоугольника, деление отрезка пополам |