Электротехника. 07 Лекция. Сложение и вычитание синусоидальных функций с помощью комплексных чисел. Векторная диаграмма
 Скачать 138 Kb.
|
|
§4. Сложение и вычитание синусоидальных функций с помощью комплексных чисел. Векторная диаграмма. Сложим два тока i1 и i2 одинаковой частоты: 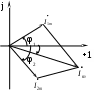 ;  ;   .  ;  ,    ;  , . .Векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе. §5. Закон Ома в комплексной форме для резистивного, индуктивного и ёмкостного элементов. А  . Резистивный элемент. Ток через R  .По закону Ома напряжение на R:  , (1)где амплитуды тока и напряжения связаны соотношением:  (2).Ток и напряжение на R совпадает по фазе. Разделив (2) на  , получим соотношение для действующих значений напряжения и тока для R: (3)В комплексной форме:  и  .Тогда закон Ома в комплексной форме: 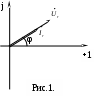  (4)Б. Индуктивный элемент. При прохождении синусоидального тока  через L, по закону электромагнитной индукции напряжение на L равно:  (5)Для амплитуд:  (6)Для действующих значений тока и напряжения (разделив для этого (6) на 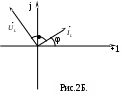): (7)   На рис.2А видно график мгновенных значений синусоидальных тока и напряжения на L. Синусоидальный ток iL отстаёт по фазе от синусоидального напряжения на π/2 – на четверть периода. Величина XL=ωL в (7) называют индуктивным сопротивлением (измеряется в Омах), а обратную величину bL=1/ωL – называют индуктивной проводимостью (измеряется в Ом-1 – См (сименсах)). В комплексной форме:  и  .На рис.2Б показана векторная диаграмма для L. Вектор комплексного значения тока  отстаёт по фазе от вектора комплексного значения напряжения  на четверть периода (π/2).Закон Ома в комплексной форме для L:  (8)или  (9)Величина jωL=jXL – называют комплексным сопротивлением индуктивного элемента, а обратная ей величина 1/ jωL=-jbL – комплексной проводимостью индуктивного элемента. В. Ёмкостной элемент. Если приложить к конденсатору напряжение не меняющееся во времени, то величина заряда на пластине равна: q=Cu (на другой пластине заряд –q), где С – ёмкость конденсатора. Ток через конденсатор в этом случае не проходит. Если же напряжение на конденсаторе меняется во времени  , тогда заряд  – меняется во времени, и , следовательно, через С пройдёт ток: (10)Для амплитуд:  ,для действующих значений:  (11)XC – называют ёмкостным сопротивлением (Ом); b  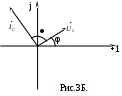 C – называют ёмкостной проводимостью (См).В противоположность индуктивности ёмкостное сопротивление уменьшается с увеличением частоты синусоидального тока. При постоянном напряжении сопротивление бесконечно велико. Из (5) и рис.3 видно, что для ёмкостного элемента синусоидальное напряжение UCотстаёт по фазе от синусоидального тока iCна π/2. В комплексной форме:  ;  .Закон Ома для ёмкостного элемента в комплексной форме:  (12)Величину 1/jωC=-jXC – называют комплексным сопротивлением ёмкостного элемента, а величину jωC=jbC – комплексной проводимостью. |