Начало. Векторы-начало. Сложение векторов Для сложения векторов есть два способа
 Скачать 71.17 Kb.
|
|
Сложение векторов Для сложения векторов есть два способа. 1. Правило параллелограмма. Чтобы сложить векторы  и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и . Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю. 2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 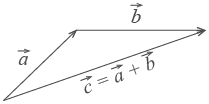и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и . По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.  Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F. При сложении векторов  и  получаем:  Вычитание векторов Вектор 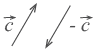 направлен противоположно вектору  . Длины векторов и равны. Теперь понятно, что такое вычитание векторов. Разность векторов 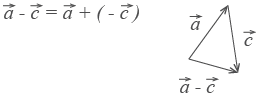и - это сумма вектора и вектора  . Умножение вектора на число При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля. Скалярное произведение векторов Векторы можно умножать не только на числа, но и друг на друга. Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. 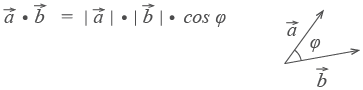 Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:  Если векторы перпендикулярны, их скалярное произведение равно нулю. А вот так скалярное произведение выражается через координаты векторов и : Из формулы для скалярного произведения можно найти угол между векторами:  Эта формула особенно удобна в стереометрии. |