билеты геометрия 7 класс. Смежные углы

• Название: Смежные углы
• Дата: 10.04.2022
• Размер: 1.61 Mb.
• Имя файла: билеты геометрия 7 класс.doc
• Тип: Задача; #459283
• страница: 2 из 4

(п. 37) Пусть ВА - перпендикуляр, опущенный из точки В на прямую а, и С – любая точка на прямой а, отличная от точки А (основание перпендикуляра). Отрезок ВС называется наклонной, проведенной из точки В к прямой а. Точка С называется основанием наклонной, а отрезок АС — проекцией наклонной.


Расстоянием от точки В до прямой а называется длина перпендикуляра из этой точки к данной прямой, т.е. длина отрезка ВА.
Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой. Поэтому расстояние от точки В до прямой а является наименьшим из расстояний от точки В до любой из точек прямой а.

2. 
   (п.25) Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰, то прямые параллельны.
   

Дано:прямые а и b, с –секущая,односторонние углы∠1 +∠4 = 180⁰.

Доказать,что а||b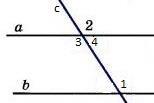




Доказательство:∠1 +∠4 = 180⁰(по условию),∠3 +∠4 = 180⁰(смежные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b. Ч.т.д.
3. Два внешних угла треугольника равны (∠1 = ∠2). Периметр равен 74см, а одна из сторон АС = 16см. Найдите две другие стороны треугольника.
Решение: По условию ∠1 = ∠2, следовательно ∠А = ∠С (как смежные с равными углами), а значит ∆АВС – равнобедренный, т.е. АВ = ВС = х. Периметр – это сумма всех сторон, составим уравнение:

• 
  + х + 16 = 74см
  

2х = 74 – 16

2х = 58

• 
  = 29см = АВ = ВС. Рассмотрим другой случай:
  

Билет. 5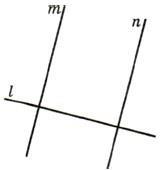

1. 
   (п. 24) Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: m || n.
   

Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой.
Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Все перпендикуляры к одной и той же прямой параллельны между собой.
Два отрезка называются параллельными, если они лежат на параллельных прямых.

2. 
   (п.15) Если 2 стороны и угол между ними одного треугольника соответственно равны 2 сторонам и углу между ними другого треугольника, то такие треугольники равны.
   

Дано: ∆АВС и∆А₁В₁С₁,у них АВ=А₁В₁,АС=А₁С₁,∠А=∠А₁.Доказать,что∆АВС= ∆А₁В₁С₁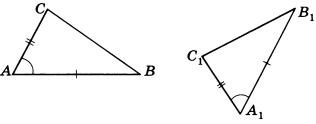




Доказательство:Наложим∆АВС на∆А₁В₁С₁так,чтобывершина А совпала с вершиной А₁. Так как по условию ∠А = ∠А₁, то луч АВ наложится на луч А₁В₁, а луч АС на луч А₁С₁. Еще по условию АВ=А₁В₁, значит точка В совпадет с точкой В₁, АС=А₁С₁, значит точка С совпадет с точкой С₁. Все три точки у треугольников совпали, значит они равны. Ч.т.д.
3. В равнобедренном ∆АВС с основанием ВС проведена медиана АМ. Найдите её длину, если периметр ∆АВС = 32см, а периметр ∆АВМ равен 24см.

Р 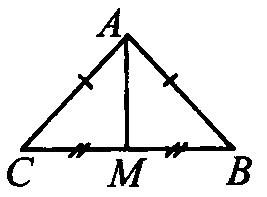ешение: Р_АВС = АВ+ВС+АС
32 = 2АВ+2ВМ (т.к. АВ=АС и ВМ=МС) 32 = 2(АВ + ВМ)
16 = АВ + ВМ.

Р_АВМ = АВ+ВМ+АМ, 24 = 16 + АМ, следовательно АМ = 24 – 16 = 8см.

Ответ: АМ = 8см.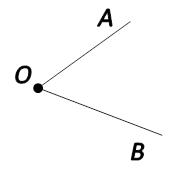




Билет. 6
1. (п. 3-4) Луч (полупрямая) – часть прямой, имеющая начало и не имеющая конца. Угол – это геометрическая фигура, которая состоит из двух лучей исходящих из одной вершины.
Вершина угла —это точка,в которой два луча берут начало. Стороны угла —это лучи,которые образуют угол.
Например, вершина угла — точка O. Стороны угла — OA и OB. Для обозначения угла в тексте используется символ: ∠AOB.

Способы обозначения углов:

1. Одной заглавной	2. Тремя заглавными латинскими буквами, которыми	3. Двумя строчными
латинской буквой,	обозначены вершина и две точки, расположенные на	латинскими буквами.
указывающейего	сторонах угла. Угол: ∠AOD.	Угол: ∠fn
вершину. Угол: ∠O.
	Называть угол можно с любого края, но НЕ с
	вершины. Угол с рисунка выше имеет два названия:
	∠AOD и ∠DOA.
	Вершина угла должна всегда находиться в середине
	названия!!!

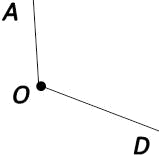Единица измерения углов — градусы. Углы измеряют с помощью специального прибора – транспортира. Для обозначения градусов в тексте используется символ: °, например ∠В = 50°
Виды углов

Вид угла	Размер в градусах	Пример
Прямой	Равен 90°
Острый	Меньше 90°
Тупой	Больше 90°
Развернутый	Равен 180°

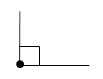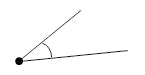2. (п. 18) В равнобедренном треугольнике углы при основании равны.

Д 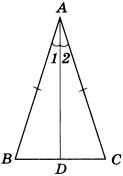ано: ∆АВС,АВ=АС.

Доказать,что∠В=∠С.
Доказательство:В∆АВС из вершины А проведем биссектрису АД.ТреугольникиABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD – общая сторона, ∠1 = ∠2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠В = ∠С. Ч.т.д.

3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210⁰. Найдите все углы. Решение: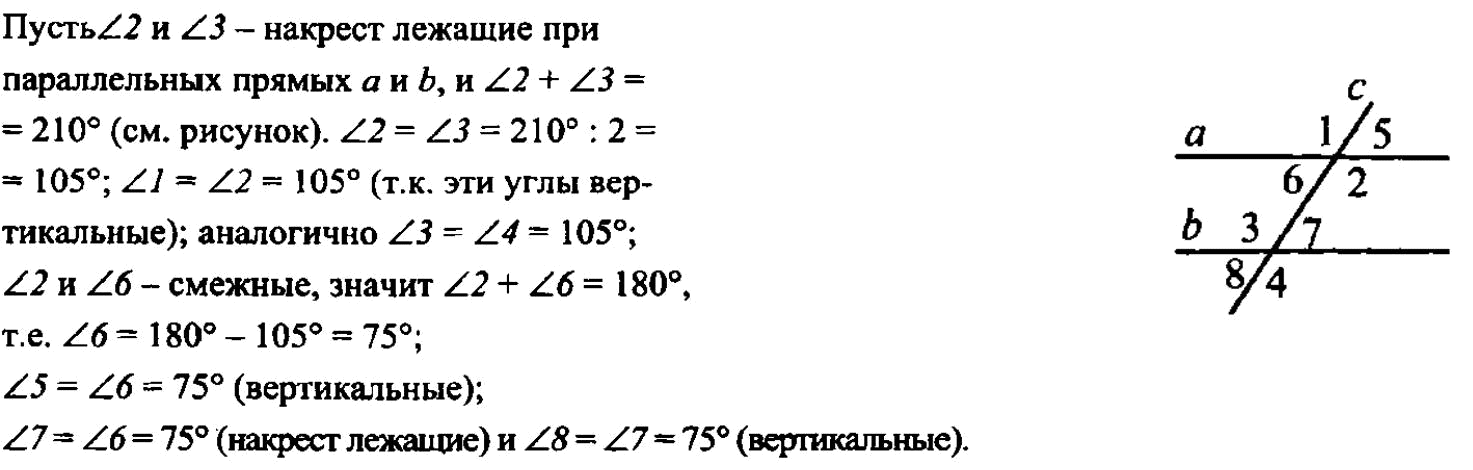




Билет. 7

1. (п. 25) Прямая с называется секущей к прямым а и b, если она пересекает их в двух точках.
При пересечении двух параллельных прямых секущей, образуются восемь углов, которые попарно называются:

1.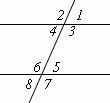 
   с оответственные углы (они попарно равны:∠1 =∠5;∠2 =∠6;∠3 =∠7;∠4 =∠8);
   

2. 
   накрест лежащие углы (4 и 5; 3 и 6);они тоже попарно равны;
   

3. 
   односторонние углы (3 и 5; 4 и 6);их сумма равна180
   

(∠3 + ∠5 = 180; ∠4 + ∠6 = 180).
2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆АВС и∆А₁В₁С₁,у них АВ=А₁В₁,∠А=∠А₁,∠В=∠В₁Доказать,что∆АВС= ∆А₁В₁С₁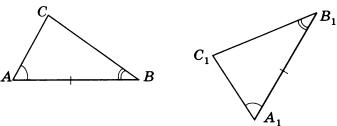




Доказательство:Наложим∆АВС на∆А₁В₁С₁так,чтобысторона АВ совпала со стороной А₁В₁ (по условию они равны, значит совпадут). Так как по условию ∠А = ∠А₁ и ∠В = ∠В₁, то сторона АС наложится на луч А₁С₁, а сторона ВС на луч В₁С ₁. Вершина С окажется лежащей как на луче А₁С₁, так и на луче В₁С₁, а значит совпадет с

вершиной С₁. Все три точки у треугольников совпали, значит они равны. Ч.т.д.
3. АМ – биссектриса ∆АВС. Через точку М проведена прямая, параллельная АС и пересекающая сторону АВ в точке Е. Докажите, что ∆АМЕ равнобедренный.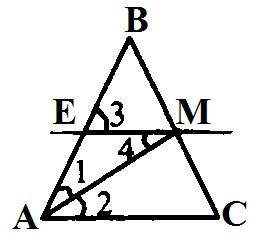




Доказательство: АС || ЕМ, значит ∠1 = ∠3 (как соответственные углы), ∠2 = ∠4 (как накрест лежащие углы), ∠1 = ∠2 (т.к. АМ – биссектриса).
Следовательно, ∠1 = ∠4, а это углы при основании в ∆АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч.т.д.
Билет. 8

1. 
   Постройте треугольник по 2 сторонам и углу между ними. Смотри презентацию, слайд 10.
   

2. 
   (п. 30) Сумма углов в треугольнике 180⁰.
   

Дано: ∆АВС.

Доказать,что∠А+∠В+∠С= 180⁰.
Доказательство:Проведем через вершину В прямую а,параллельную стороне АСОчевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.

∠4 + ∠2 + ∠5 = 180° (*).
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС.

Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем: ∠l + ∠2 + ∠3 = 180°,

или ∠A + ∠B + ∠C = 180°. Ч.т.д.
3. На биссектрисе угла А взята точка Е, а на сторонах этого угла точки В и С так, что ∠АЕС = ∠АЕВ. Докажите, что ВЕ = СЕ.
Доказательство: Рассмотрим ∆АСЕ и ∆АВЕ.
У них: ∠ВАЕ=∠САЕ, т.к. АЕ – биссектриса угла А, ∠АЕС = ∠АЕВ (по условию). Сторона АЕ – общая.

Значит ∆АСЕ = ∆АВЕ по II признаку. Тогда ВЕ = СЕ. Ч.т.д.


Билет. 9
1. (п. 21) Окружность – геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами. Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности. Круг – часть плоскости, лежащая внутри окружности.

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для изображения окружности на чертеже пользуются циркулем.

2. (п. 33) Каждая сторона треугольника меньше суммы двух других сторон.

Дано: ∆АВС.
Доказать,что АВ<АС+СВ.
Доказательство:Строим отрезок СМ=ВС на продолжении стороны АС.В равнобедренном ВСМ ∠1 = ∠2 (по свойству углов в равнобедренном треугольнике). ∠1 < ∠АВМ, значит и ∠2 < ∠АВМ.
Рассмотрим треугольник АВМ. Так как в треугольнике против большего угла лежит большая сторона, то АВ<АМ,АВ<АС+СМ,АВ<АС+ВС.
(т.к. СМ = ВС). Ч.т.д.

3. Отрезки АВ и СD пересекаются в их общей середине. Докажите, что прямые АС и ВD параллельны.
Доказательство:

О


Билет. 10

1. 
   (п. 27-28) Аксиома – это такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на основе которых строят все дальнейшие суждения и доказательства.
   

Аксиома параллельных прямых: Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.