билеты геометрия 7 класс. Смежные углы

• Название: Смежные углы
• Дата: 10.04.2022
• Размер: 1.61 Mb.
• Имя файла: билеты геометрия 7 класс.doc
• Тип: Задача; #459283
• страница: 4 из 4

Билет. 18

1. 
   (п.35) Признаки равенства прямоугольных треугольников:
   

1. 
   по двум катетам: Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
   

2. 
   по катету и гипотенузе: Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
   

3. 
   по гипотенузе и острому углу: Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
   

4. 
   по катету и острому углу: Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
   

2. (п. 11) Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.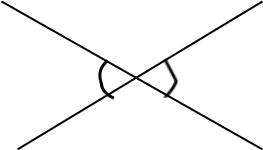

Теорема: Вертикальные углы равны.		2
Доказательство: ∠1 + ∠2 = 1800 (смежные),	1	3
∠3 + ∠2 = 1800 (смежные),	→ ∠1 = ∠3. Ч.т.д.

3. В равнобедренном ∆АВС с основанием АС = 37см, внешний угол при вершине В равен 60⁰. Найти расстояние от вершины С до прямой АВ.

Д 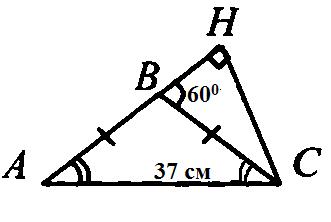ано:∆АВС–равнобед.,внешний∠НВС= 60⁰,АС=37см,СНАВ(т.к.это расстояние).

Найти:длину СН.
Решение:По свойству внешнего угла∠НВС=∠А+∠С= 60⁰.А т.к.∆АВС – равнобед., то ∠А = ∠С = 60⁰/2 = 30⁰ (углы при основании). В прямоугольном треугольнике АНС, ∠А = 30⁰, значит катет лежащий
напротив него равен половине гипотенузы, т.е. СН  ¹₂ АС  37 : 2 18,5см. Ответ: СН = 18,5см.
Билет. 19

1. 
   Как построить треугольник по трем сторонам. Смотри презентацию, слайд 8. Задача имеет решение только когда выполняется неравенство треугольника, т.е. сумма двух любых сторон должна быть больше третьей стороны.
   

2. 
   (п.32) В треугольнике против большей стороны лежит больший угол.
   

Д 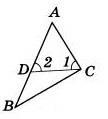ано: ∆АВС,АВ>АС.

Доказать,что∠С>∠В
Доказательство:Отложим на стороне АВ отрезокAD=АС.Так какAD <АВ,тоточка D лежит между точками А и В. Следовательно, ∠1 является частью ∠С и, значит, ∠C > ∠1. Угол 2 – внешний угол ∆BDC, поэтому ∠2 > ∠В. ∠1 = ∠2 как углы
при основании равнобедренного треугольника ADC. Таким образом, ∠С > ∠1, ∠1 = ∠2, ∠2 > ∠B. Отсюда следует, что ∠С > ∠В. Ч.т.д.
3. Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.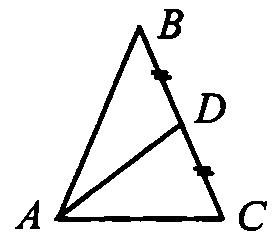




Решение: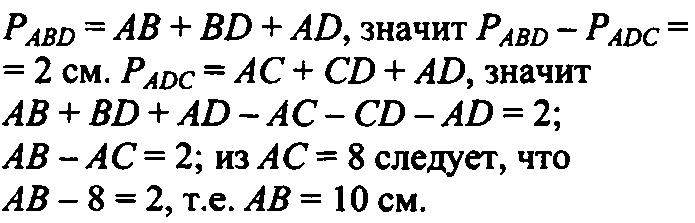


Билет. 20

1. 
   Как построить биссектрису данного угла. Смотри презентацию, слайд 4.
   

2. 
   (п.18) В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
   

Д 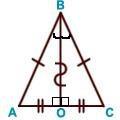ано: ∆АВС,АВ=ВС,ВОАС(высота).Доказать,что ВО–медиана и биссектриса.

Доказательство: Рассмотрим ∆ABO и ∆CBO. У них:
AB = BC (по условию), ∠A = ∠С = х (углы при основании в равноб. ∆), ∠AВО = ∠СВО = 90⁰ – х (по теореме о сумме углов в ∆).
Значит эти треугольники равны по 2 признаку. Следовательно, AO = OС, а значит BO – медиана.

Далее, ∠AВО = ∠СВО = 90⁰ – х, значит BO – биссектриса. Ч.т.д.
3. В прямоугольном треугольнике АВС с прямым углом С внешний угол при вершине А равен 120⁰, АС + АВ = 18см. Найти АС и АВ.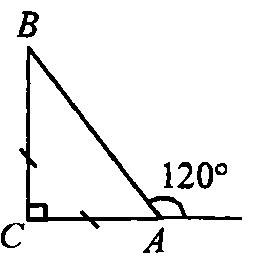




Решение:В∆АВС:∠А= 180⁰–120⁰= 60⁰(смежные).
∠В = 180⁰ – 90⁰ – 60⁰ = 30⁰ (по теореме о сумме углов в ∆). Следовательно, катет лежащий напротив ∠В равен половине гипотенузы, т.е. АС  ¹₂ АВ или АВ = 2АС.
По условию АС + АВ = 18см, значит АС + 2АС = 18см. Отсюда 3АС = 18см, АС = 6см. Тогда АВ = 2АС = 2*6 = 12см. Ответ: АС = 6см, ВС = 12см.


Билет. 21

1. 
   Как построить середину отрезка. Смотри презентацию, слайд 7.
   

2. 
   (п.25) Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰, то прямые параллельны.
   

Дано:прямые а и b, с –секущая,односторонние углы∠1 +∠4 = 180⁰.

Доказать,что а||b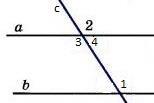




Доказательство:∠1 +∠4 = 180⁰(по условию),∠3 +∠4 = 180⁰(смежные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b. Ч.т.д.
3. В треугольниках АВС и МКЕ отрезки СО и ЕН медианы, ВС = КЕ, ∠В = ∠К и ∠С = ∠Е. Доказать, что ∆АСО = ∆МЕН.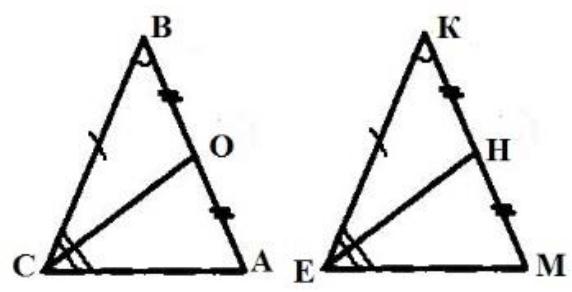




Доказательство:По условию:ВС=КЕ,∠В=∠К и∠С=∠Е,значит, ∆АВС = ∆МКЕ (по 2 признаку). Следовательно у этих треугольников равны соответственные стороны и углы, т.е. АВ = МК, а значит и АО = МН, ∠А = ∠М и АС = МЕ. Тогда ∆АСО = ∆МЕН (по 1 признаку).
Билет. 22
1. (п. 21) Окружность – геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами. Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности. Круг – часть плоскости, лежащая внутри окружности.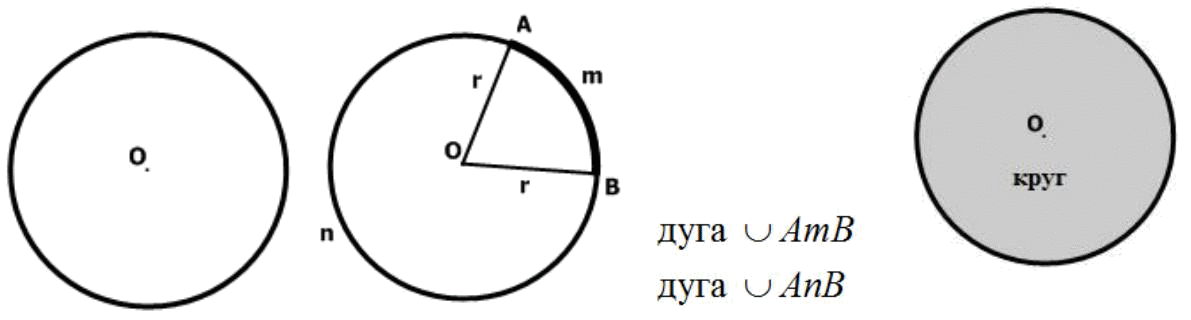



Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для изображения окружности на чертеже пользуются циркулем.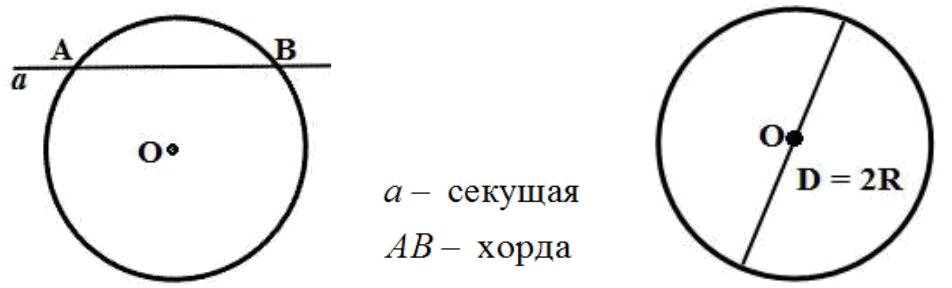



2. (п. 34) Свойства прямоугольных треугольников:

1⁰. Сумма двух острых углов в прямоугольном треугольнике равна 90⁰.
Доказательство:В самом деле,сумма углов треугольника равна180⁰,а т.к.прямой угол= 90⁰,тосумма двух других углов в треугольнике = 90⁰.
2⁰. Катет прямоугольного треугольника, лежащий против угла в 30⁰, равен половине гипотенузы.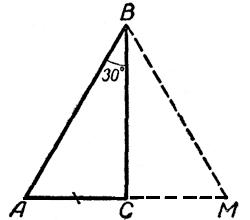




Доказательство:Пусть в прямоугольном∆АСВ∠В=30°.Тогда другойего острый угол будет равен 60°. Докажем, что катет АС равен половине гипотенузы АВ.
Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник – равносторонний. Катет АС равен половине AM, а так как AM равняется АВ, то катет АС будет равен половине гипотенузы АВ. Ч.т.д.
3⁰. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30⁰.
3. Найти все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42⁰.

Р 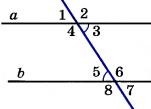ешение:Пусть а ǀǀ b, с – секущая,∠1 = 42⁰.Тогда∠3 =∠1 = 42⁰(вертикальные),

∠5 = ∠3 = 42⁰ (накрест лежащие), ∠7 = ∠5 = 42⁰ (вертикальные), ∠8 и ∠7 смежные,

значит ∠8 = 180⁰ – ∠7 = 180⁰ – 42⁰ = 138⁰, ∠6 = ∠8 = 138⁰ (вертикальные),

∠2 = ∠6 = 138⁰ (соответственные), ∠4 = ∠2 = 138⁰ (вертикальные).
Билет. 23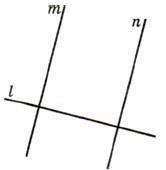




1. (п. 24) Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: m || n.
Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой.
Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Все перпендикуляры к одной и той же прямой параллельны между собой.

Два отрезка называются параллельными,если они лежат на параллельных прямых.
2. (п.32) В треугольнике против большего угла лежит большая сторона.

Д 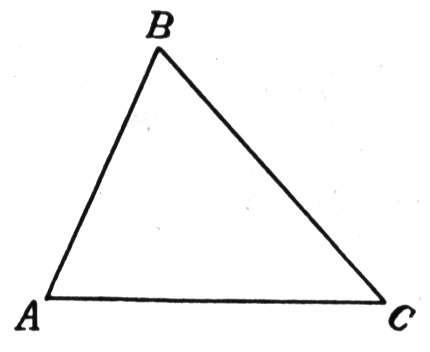ано: ∆АВС,∠С>∠В.

Доказать,что АВ>АС.
Доказательство:Предположим,что это не так.

Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆АВС
– равнобедренный, а значит углы при основании равны, т.е. ∠С=∠В, а это противоречит условию, что ∠С > ∠В. Во втором случае получаем, что ∠С < ∠В (т.к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше предположение неверно, и, следовательно, АВ > АС. Ч.т.д.
3. Найдите углы при основании МР равнобедренного ∆МОР, если МК – его биссектриса и ∠ОКМ = 96⁰. Решение:∠РКМ=180⁰–96⁰= 84⁰(смежный с∠ОКМ).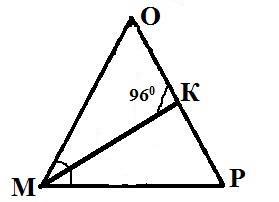




Пусть ∠КРМ = х, тогда ∠КМР = 0,5х, т.к. МК – биссектриса и ∠М = ∠Р (углы при основании в равноб. ∆). По теореме о сумме углов в ∆МКР:

х + 0,5х + 84⁰= 180⁰.Отсюда, 1,5х = 96⁰, х = 64⁰.
Ответ: углы при основании равны 64⁰.

Билет. 24
1. (п. 14) Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его
сторонами. Виды треугольников:



2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Д 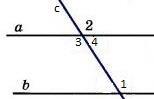ано:прямые а и b, с –секущая,соответственные углы∠1 =∠2.

Доказать,что а||b
Доказательство:∠1 =∠2 (по условию),∠2 =∠3 (вертикальные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b.
Ч.т.д.
3. В равнобедренном треугольнике одна сторона равна 25см, а другая 10см. Какая из них является основанием?
Решение:В треугольнике каждая сторона должна быть меньше суммы двух других.Тогда,если основаниеравно 10 см, то каждая сторона удовлетворяет такому условию. Но если основание равно 25 см, то 25 см > 10 см + 10 см - это не верно. Значит, есть только одно правильное решение.
Ответ: основание равно 10 см.
Билет. 25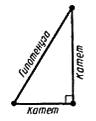

1. 
   (п. 31) Прямоугольный треугольник – это треугольник, у которого один угол прямой, т.е. равен 90⁰.
   

Сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны - катетами. Гипотенуза всегда большего любого из катетов, т.к. лежит напротив большего угла в треугольнике.

2. 
   (п. 30) Сумма углов в треугольнике 180⁰.
   

Д 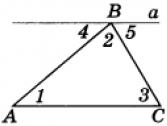ано: ∆АВС.

Доказать,что∠А+∠В+∠С= 180⁰.

Доказательство:Проведем через вершину В прямую а,параллельную стороне АСОчевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.

∠4 + ∠2 + ∠5 = 180° (*).

Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей

АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей
ВС. Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем:
∠l + ∠2 + ∠3 = 180°, или ∠A + ∠B + ∠C = 180°. Ч.т.д.	Д
А
3. Прямые АВ и СД пересекаются в точке О, ∠AОС = 580. Найдите ∠ВОД.	О
Решение:∠ВОД=∠AОС= 580,т.к.они вертикальные.	580
С	В