Задача по физике. Пример 3. Смотри в загрузках

• Название: Смотри в загрузках
• Анкор: Задача по физике
• Дата: 12.03.2023
• Размер: 151.87 Kb.
• Имя файла: Пример 3.docx
• Тип: Решение; #982842

Пример 3. Из одной точки одновременно бросили два тела под углами α1 = 60° и α2 = 45° к горизонту с начальными скоростями v1 = 40 м/с и v2 = 50 м/с . Траектории тел лежат в одной плоскости (рис. 3). На каком расстоянии l друг от друга будут находиться тела через время t = 3,0 с ? Р е ш е н и е

Смотри в загрузках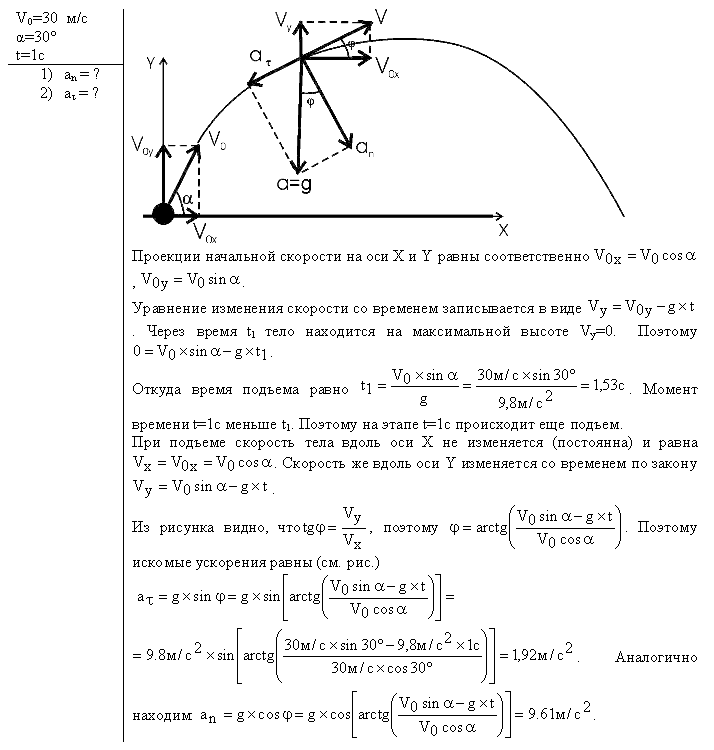



http://exir.ru/other/chertov/metodichka/molekulyarnaya_fizika_termodinamika.htm

Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.



вижение тела, брошенного под углом к горизонту (бросок)

Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом 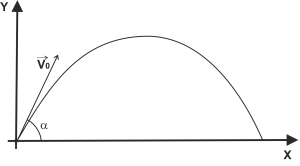  к оси ОХ (рис. 1).



Рис. 1. Тело бросили под углом к горизонту

Классическая постановка задач на подобную тематику: тело бросили под углом   к горизонту с начальной скоростью  , найти различные параметры движения.

Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).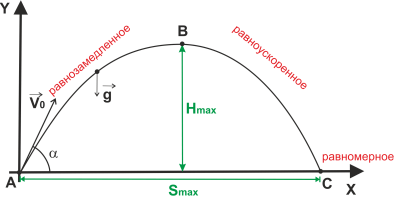



Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)

Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ (  (м/ ), а на ось OY (  (м/ ).

Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.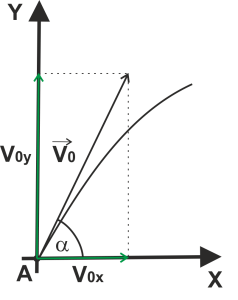


Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим   и  . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( ), можем найти значения необходимых нам проекций:

• 
   (1)
  
• 
   (2)
  

Вернёмся к рисунку 2. Попробуем найти полное время полёта ( ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:

 (3)

 — т.к. время движения от точки А до B, и от B до C одинаково. Тогда:

 (4)

И, учитывая (2):

 (5)

Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( ).

Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время  :

 (6)

А с учётом (1) и (5):

 =  =  (7)

Перейдём к максимальной высоте полёта ( ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( ) в течение времени  , формируем уравнение:

 (8)

С учётом (5):

 =   (9

Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.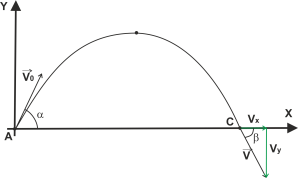



Рис. 4. Тело бросили под углом к горизонту (конечная скорость)

Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела   направлена под неким углом  . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:

 (10)

Найдём компоненты вектора  . Т.к. движение вдоль оси OX равномерное, значит,  , используя (1):

 (11)

Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время  , тогда:

 (12)

Используя (5), получим:

 (13)

Подставим (12) и (13) в (10):

 =   =   (14)

Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом  .

Вывод: 

• 
  для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
  
• 
  представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).
  

: