Решение системы уравнений методом Гаусса C. Содержани Введение 2 Индивидуальное задание 3 1Выполнение задачи 3 Работа программного кода 4 Заключение 5 Введение 3 Индивидуальное задание 4 1 Выполнение задачи 4 Работа программного кода 5 Заключение 6 Приложение А

• Название: Содержани Введение 2 Индивидуальное задание 3 1Выполнение задачи 3 Работа программного кода 4 Заключение 5 Введение 3 Индивидуальное задание 4 1 Выполнение задачи 4 Работа программного кода 5 Заключение 6 Приложение А
• Анкор: Решение системы уравнений методом Гаусса C
• Дата: 08.07.2022
• Размер: 48.25 Kb.
• Имя файла: Praktika.docx
• Тип: Решение; #627367

Содержани

Введение 2

1.Индивидуальное задание 3

1.1Выполнение задачи 3

2.Работа программного кода 4

Заключение 5

Введение 3

1. Индивидуальное задание 4

1.1 Выполнение задачи 4

2. Работа программного кода 5

Заключение 6

Приложение А 7

Введение

Целью производственной практики является закрепление теоретических знаний, приобретенных студентами в рамках учебного процесса. Для достижения поставленной цели требуется решить следующие задачи:

1. 
   Изучить пособие “Основы вычислительной математики” Демидович Б.П, Марон И.А
   
2. 
   Разработать программу на языке программирования C++ по индивидуальному заданию.
   

1. Индивидуальное задание

Решение системы уравнений методом Гаусса.

1. Выполнение задачи

Выполнение:

-Подключаем библиотеку для реализации потокового ввода и вывода данных в консоли.

- Подключаем пространство имён using namespace std;

- Функция sysout для вывода системы уравнений.

- Функция gauss для нахождения корней системы уравнений с помощью метода Гаусса.

- Поиск строки с максимальным a[i][k].

- Перестановка строк.

- Проверка на нулевые диагональные переменные.

- Нормализация уравнений.

- Для нулевого коэффициента пропустить.

- Запрет уравнению вычитать само из себя.

- Обратная подстановка

- Функция main

- Подключение русского языка.

- Ввод уравнений.

- Очистка памяти которая была занята динамическими массивами.

Листинг программного кода предоставлен приложении А.

2. Работа программного кода

Проверка работы программы предоставлена на рис. 1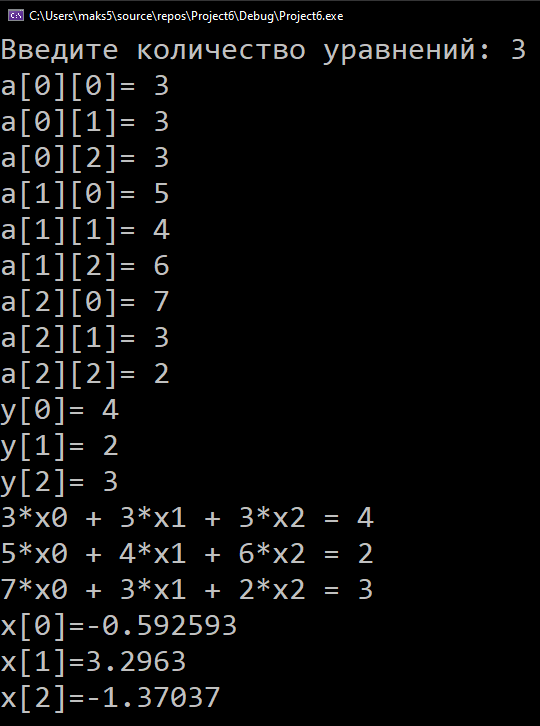


Рисунок 1- скриншот консоли программы Microsoft Visual Studio

Заключение

Во время производственной практики были закреплены теоретические знания, приобретенных студентами в рамках учебного процесса. Для достижения поставленной цели были решены следующие задачи:

1. 
   Изучить пособие “Основы вычислительной математики” Демидович Б.П, Марон И.А
   
2. 
   Разработать программу на языке программирования C++ по индивидуальному заданию.
   

Приложение А

#include

using namespace std;

// Вывод системы уравнений

void sysout(double** a, double* y, int n)

{

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

{

cout << a[i][j] << "*x" << j;

if (j < n - 1)

cout << " + ";

}

cout << " = " << y[i] << endl;

}

return;

}

double* gauss(double** a, double* y, int n)

{

double* x, max;

int k, index;

const double eps = 0.00001; // точность

x = new double[n];

k = 0;

while (k < n)

{

// Поиск строки с максимальным a[i][k]

max = abs(a[k][k]);

index = k;

for (int i = k + 1; i < n; i++)

{

if (abs(a[i][k]) > max)

{

max = abs(a[i][k]);

index = i;

}

}

// Перестановка строк

if (max < eps)

{

// нет ненулевых диагональных элементов

cout << "Решение получить невозможно из-за нулевого столбца ";

cout << index << " матрицы A" << endl;

return 0;

}

for (int j = 0; j < n; j++)

{

double temp = a[k][j];

a[k][j] = a[index][j];

a[index][j] = temp;

}

double temp = y[k];

y[k] = y[index];

y[index] = temp;

// Нормализация уравнений

for (int i = k; i < n; i++)

{

double temp = a[i][k];

if (abs(temp) < eps) continue; // для нулевого коэффициента пропустить

for (int j = 0; j < n; j++)

a[i][j] = a[i][j] / temp;

y[i] = y[i] / temp;

if (i == k) continue; // уравнение не вычитать само из себя

for (int j = 0; j < n; j++)

a[i][j] = a[i][j] - a[k][j];

y[i] = y[i] - y[k];

}

k++;

}

// обратная подстановка

for (k = n - 1; k >= 0; k--)

{

x[k] = y[k];

for (int i = 0; i < k; i++)

y[i] = y[i] - a[i][k] * x[k];

}

return x;

}

int main()

{

double** a, * y, * x;

int n;

setlocale(LC_ALL, "Russian");

cout << "Введите количество уравнений: ";

cin >> n;

a = new double* [n];

y = new double[n];

for (int i = 0; i < n; i++)

{

a[i] = new double[n];

for (int j = 0; j < n; j++)

{

cout << "a[" << i << "][" << j << "]= ";

cin >> a[i][j];

}

}

for (int i = 0; i < n; i++)

{

cout << "y[" << i << "]= ";

cin >> y[i];

}

sysout(a, y, n);

x = gauss(a, y, n);

if (x != 0)

{

for (int i = 0; i < n; i++) {

cout << "x[" << i << "]=" << x[i] << endl;

}

}

cin.get();

cin.get();

for (int i = 0; i < n; i++) {

delete[] a[i];

}

delete[] a;

delete[] x;

delete[] y;

return 0;

}