Отчет по геодезии. Бр.3-Рпзс-19-6.Отчет. Содержание работы
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
|
Основные правила по эксплуатации нивелиров Невзирая на то, что основная сфера применения этой измерительной техники в профессиональных кругах, зачастую ее активно используют и в быту. Скажем, нивелир помогает сделать измерения при строительстве домиков на дачных участках, сборке мебели, размещении полок на стене, оклейке обоев и при других работах по обустройству дома. Все расчеты будут точными, а значит, и результат будет соответствующий. Когда Ваши друзья спросят, сколько же стоило нанять мастеров для выполнения этих работ, представьте себе: как гордо это будет звучать, что все это было сделано своими руками! Безусловно, в профессиональной сфере часто используются одни и те же приборы, чаще всего, оптические, а в быту особенно популярны лазерные нивелиры. А теперь стоит по порядку как следует разобраться, какие нюансы существуют в работе с теми и другими устройствами, дабы Вам было легче добиться отличного результата на практике. Оптические нивелиры Помимо строительства, оптические нивелиры широко применяются при топографической съемке местности, выполнении геодезических и ремонтно-дорожных работ. Данные устройства оборудованы зрительной трубой, в которой имеется окуляр и сетка со специальной шкалой. Перед началом измерений необходимо настроить зрительную трубу так, чтобы изображение в окуляре было максимально отчетливым. Менять положение трубы, настраивать изображение окуляра необходимо особыми регулировочными винтами, при этом всегда смотреть в окуляр. Чтобы усовершенствовать видимость при настройке, можно воспользоваться белым листом, расположив его на маленьком расстоянии от зрительной трубы. Черные линии шкалы должны быть видны максимально отчетливо, а все деления отлично видны. Только в этом случае можно произвести верный и оптимально точный замер.. Лазерные нивелиры В последнее время строители, плотники и монтажники все чаще используют лазерный нивелир - более усовершенствованный, по сопоставлению с оптическим. И этому есть логическое объяснение. Подобный прибор отличается удобством в эксплуатации, успешно совладать с которым может даже новичок в этом деле. Ведь все замеры выполняются всего лишь силами одного человека! Достаточно будет навести лазер на объект, и на его поверхность будет спроецирован луч, по расположению которого будет определяться требуемая высота либо выполняться разметка. Именно поэтому в последнее время лазерные нивелиры все чаще стали приобретаться для частого применения в бытовых целях. Если Вы задались целью выложить плитку в ванной комнате, при помощи нивелира будет легко сделать ровную разметку. Особенно это важно при укладке первого ряда. Если он будет неровным, последующая работа пойдет насмарку. Модели нивелиров с дисплеем особенно удобны в применении: все данные выводятся на экран (поэтому их не надо фиксировать в журнале). Во время измерения используется рейка со специальными штрих кодами, которые отлично «прочитываются» датчиками, а полученная информация передается в микропроцессор. Многие модели техники оснащены программой, которая позволяет перенести данные на персональный компьютер через USB-кабель, чтобы применять в дальнейших расчетах. Геометрическое нивелирование Заключается в использовании инструментальной способности построения горизонтального луча (оси) конструкцией нивелиров для выполнения высотных измерений. Характерным способом геометрического нивелирования является так называемый метод «из середины» с использованием нивелирных реек со специально нанесенными на них шкалами. Типовая схема его показана на рис.2.7. 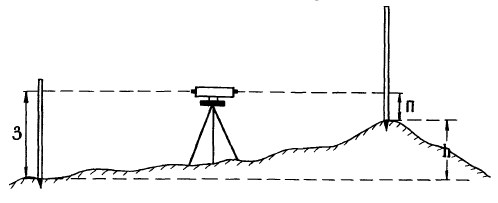 Рис.2.5. Схема геометрического нивелирования. Суть способа состоит в установлении нивелиров ориентировочно посередине между точками, на которых необходимо измерить высотные отметки. Именно на них устанавливаются в вертикальное (отвесное) положение рейки, по которым снимаются отсчеты в миллиметрах (0123). Сначала измерения осуществляют с задней (З) рейки после этого нивелир разворачивается в направлении передней точки (П). Изначально задней точкой выступает исходный репер с известным значением абсолютной отметки. Превышение (h) между точками, на которых устанавливались рейки, вычисляют по формуле: h = З – П, где З – задний отсчет по рейке;П – передний отсчет. Точность снятия отсчетов по рейкам колеблется в пределах 1-2 мм при техническом нивелировании и 0,1 мм при нивелировании I класса.  Рис.2.6.Устройство нивелир Другие виды нивелирования Могут использоваться в условиях, в которых они более предпочтительны к применению. Так тригонометрическое нивелирование за счет возможности изменения наклона зрительной трубы и соответственно визирного луча в теодолитах (тахеометрах) производится на местности с характерным гористым рельефом, на возвышенностях и поверхностях где использование геометрического нивелирования просто имеет значительные физические и экономические затраты. Современные электронные приборы (тахеометры) позволяют применять тригонометрический способ в прикладных задачах передачи и определения высотных отметок на значительно удаленные и возвышающиеся предметы, сооружения, при топографических съемках. В последние годы с появлением новых методов съемок и построений плановых сетей возникли технологические и технические возможности измерений превышений между пунктами по спутниковым наблюдениям и измерениям через ГЛОНАСС и GPS. Точные их вычисления (до 1-2 см) с одновременным получением всех трех пространственных координат делают такой способ одним из ведущих в современной геодезии. Методы построения и типы высотных нивелирных сетей Можно рассматривать в ракурсе распространения единой и однозначной высотной системы координат по всей территории страны. Она имеет название Балтийская. Известно, что за ее начальную точку отсчета принят уровень Кронштадтского футштока. Все построения происходят «от общего к частному» и соединения нивелирных ходов между собой представляют высотные сети. По точности результатов измерений они подразделяются на пять типов нивелирования: I-го класса; II-го класса; III-го класса; IV-го класса; технического нивелирования. Сети I и II класса создаются как основа всей высотной системы страны. С их помощью решаются крупные научные задачи по отслеживанию вертикальных перемещений физической поверхности Земли, исследований земной поверхности, измерения уровней всех морей окружающих нашу страну. Сети III, IV класса развиваются от пунктов более высоких классов и выступают высотной основой для топосъемок, изыскательских и прикладных геодезических работ. Ориентировочная схема по развитию нивелирных сетей показана на рис.2.9 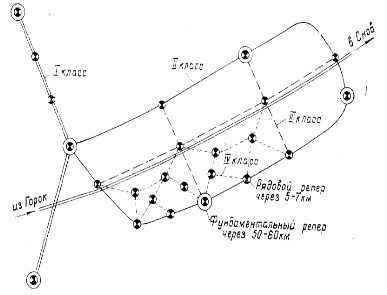 Рис.2.7. Схема высотных сетей. Сети I класса формируются из нивелирных ходов, полигонов с общей протяженностью порядка 1200 км в освоенных районах страны и 2000 км в малоосвоенных. При построении полигонов II класса их периметры составляют 400 и 1000 км соответственно. Они выстраиваются внутри полигонов I класса системой линий и ходов. Построение сетей III, IV класса опирается на пункты государственного высотного обоснования высших классов и осуществляется внутри этих полигонов. При создании высотной съемочной основы для топосъемок возможно прокладывание сетей с применением технического нивелирования. Каждый класс нивелирования исполняется с наилучшей точностью с соблюдением соответствующих требований по допустимым значениям среднеквадратических погрешностей нивелировок и предельных погрешностей в полигонах и отдельных линиях ходов. Параметры и формулы допустимых значений отображены таблице ниже, где L – длина линии хода, полигона в км. 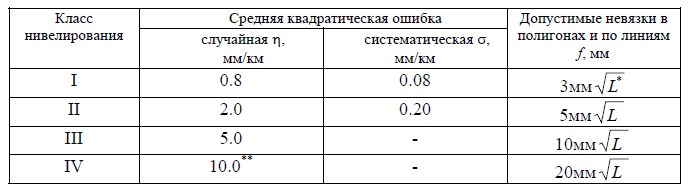 Табл.2.3 3.1.Теория ошибок при измерении Сравнение какой-либо величины с другой однородной величиной, принятой за единицу, называют измерением, а полученное при этом числовое значение –результатом измерения. Различают измерения прямые (непосредственные) и косвенные. Основное уравнение прямого измерения λ = N ∙ K где λ – результат измерения; К – значение величины, принятой за единицу измерения (сравнение); N – отвлеченное число, показывающее во сколько раз λбольше N. Косвенные измерения – такие измерения, которые получают по формулам, связывающим значения измеренных физических величин со значениями других физических величин, полученных из прямых измерений и являющихся аргументами этих формул. Уравнение косвенного измерения λ= f (λ1,λ2,λ3,...,λn).  Рис.3.1.Измерение ошибок Процесс измерений протекает во времени и определенных условиях, в нём участвуют объект измерения, измерительный прибор, наблюдатель и среда, в которой выполняют измерения. В связи с этим на результаты измерений влияют качество измерительных приборов, квалификация наблюдателя, состояние измеряемого объекта и изменения среды во времени. При многократном измерении одной и той же величины из-за влияния перечисленных факторов результаты измерений могут отличаться друг от друга и не совпадать со значением измеряемой величины. Разность между результатом измерения и действительным значением измеряемой величины называется ошибкой результата измерения. По характеру и свойствам ошибки подразделяют на: грубые; систематические; случайные. Грубые ошибки или просчеты легко обнаружить при повторных измерениях или при внимательном отношении к измерениям. Систематические ошибки – те, которые действуют по определенным законам и сохраняют один и тот же знак. Систематические ошибки можно учесть в результатах измерений, если найти функциональную зависимость и с её помощью исключить ошибку или уменьшить её до малой величины. Случайные ошибки – результат действия нескольких причин. Величина случайной ошибки зависит от того, кто измеряет, каким методом и в каких условиях. Случайными эти ошибки называются потому, что каждый из факторов действует случайно. Их нельзя устранить, но уменьшить влияние можно увеличением числа измерений. 3.2.Программное обеспечение MatLAB  Рис.3.2 Кто, когда, и для чего? Клив Моулер (Cleve Moler) разработал MATLAB как язык программирования в конце 1970-х годов когда он был деканом факультета компьютерных наук в Университете Нью-Мексико. Джон Литтл (John N. (Jack) Little) и Стив Бангерт (Steve Bangert).Совместными усилиями они создали MATLAB на C и основали в 1984 компанию The MathWorks Inc (http://www.mathworks.com/).  Рис.3.3.Интерфейс MATLAB Язык MATLAB Язык MATLAB является высокоуровневым интерпретируемым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования. Программы, написанные на MATLAB, бывают двух типов — функции и скрипты. Функции имеют входные и выходные аргументы, а также собственное рабочее пространство для хранения промежуточных результатов вычислений и переменных. Скрипты же используют общее рабочее пространство. Как скрипты, так и функции сохраняются в виде текстовых файлов и компилируются в машинный код динамически. Существует также возможность сохранять так называемые pre-parsed программы — функции и скрипты, обработанные в вид, удобный для машинного исполнения. Основной особенностью языка MATLAB являются его широкие возможности по работе с матрицами, которые создатели языка выразили в лозунге «думай векторно». Применение Математика и вычисления Разработка алгоритмов MATLAB предоставляет удобные средства для разработки алгоритмов, включая высокоуровневые с использованием концепций объектно-ориентированного программирования. В нём имеются все необходимые средства интегрированной среды разработки, включая отладчик и профайлер. Функции для работы с целыми типами данных облегчают создание алгоритмов для микроконтроллеров и других приложений, где это необходимо. Визуализация данных В составе пакета MATLAB имеется большое количество функций для построения графиков, в том числе трёхмерных, визуального анализа данных и создания анимированных роликов. Встроенная среда разработки позволяет создавать графические интерфейсы пользователя с различными элементами управления, такими как кнопки, поля ввода и другими. Внешние интерфейсы Пакет MATLAB включает различные интерфейсы для получения доступа к внешним подпрограммам, написанным на других языках программирования, данным, клиентам и серверам, общающимся через технологии Component Object Model или Dynamic Data Exchange, а также периферийным устройствам, которые взаимодействуют напрямую с MATLAB. Многие из этих возможностей известны под названием MATLAB API. COM Пакет MATLAB предоставляет доступ к функциям, позволяющим создавать, манипулировать и удалять COM-объекты (как клиенты, так и серверы). Поддерживается также технология ActiveX. Все COM-объекты принадлежат к специальному COM-классу пакета MATLAB. Все программы, имеющие функции контроллера автоматизации (англ. Automationcontroller) могут иметь доступ к MATLAB как к серверу автоматизации (англ. Automationserver). .NET Пакет MATLAB в Microsoft Windows предоставляет доступ к программной платформе .NET Framework. Имеется возможность загружать .NET сборки (Assemblies) и работать с объектами .NET классов из среды MATLAB. В версии MATLAB 7.11 (R2010b) поддерживается .NET Framework версий 2.0, 3.0, 3.5 и 4.0. Заключение В ходе 3-х недельной учебно-производственной практики, мы ознакомились с геодезическими приборами и инструментами, закрепили теоретические знания на практике, научились решать и чертить планы, освоили технологию выполнения основных геодезических работ. Приобрели навыки работы с нивелиром, электронным тахеометром, теодолитом для измерение горизонтальных и вертикальных углов. Определять географические и прямоугольные координаты решать геодезические задачи. Выполнены работы по нивелированию площади. Проходя практику, мы убедились, что геодезия и строительство тесно связаны друг с другом. Без точных геодезических измерений нельзя качественно выполнять строительно-монтажные работы, разрабатывать проект. Практика была для нас очень познавательной и интересной. Мы многому научились Литература Сборник инструкций по производству поверок геодезических приборов. - М.: Недра, 1988. - 77 с. И.Ф.Куштин, В.И.Куштин, Инженерная геодезия. Учебник для вузов, Р.: Феникс, 2002.- 425 с. Ямбаев Х.К. Геодезическое инструментоведение: Учебник для вузов. – М.: Академический Проект; Гаудеамус, 2011. – 583 с. – (Gaudeamus). Большакова В. Д. Методы н приборы высокоточных геодезических измерений в строительстве. Под ред. В. Д. Большакова. М., «Недра», 1976, 335 с. Авт.: В. Д. Большаков, И. Ю. Васютинский, Е. Б. Илюшин и др. Захаров А. И. Геодезические приборы: Справочник. — М.: Недра, 1989. —314 е. Маркшейдерско-геодезические приборы и инструменты. Федоров Б.Д. М., Недра, 1971. 288 с. Дьяконов В. П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс. 111 |
