Расчетно-графическая работа соц-эконом прогноз. Содержание Задания Теоретическая часть Расчетная часть Приложение а приложение б приложение в приложение г список используемой литературы Задания Задание 1
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
2. Расчетная часть Задание 1 Построим дискретный ряд, который показывает сколько студентов берет то или иное количество книг. В таблице 1.1 количество студентов показывает частоту. Таблица 1.1 – Количество студентов
Таблица 1.2 – Относительные частоты
Таблица 1.3 – Накопленные частности
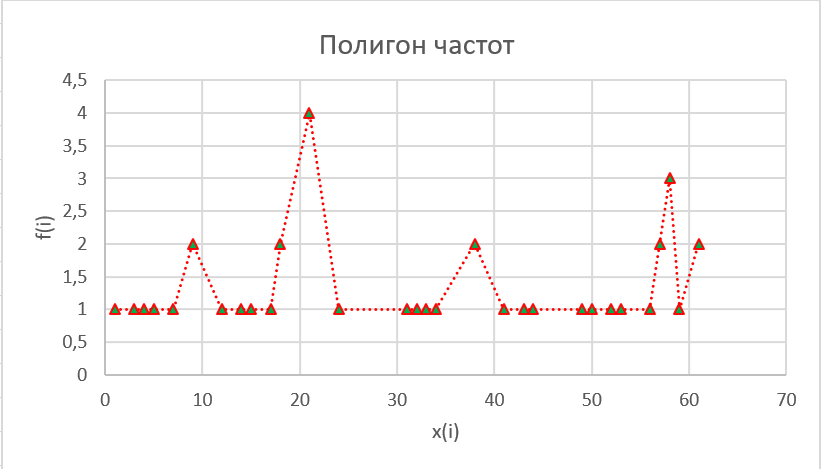 Рис. 2 – Полигон частот Для расчета средних показателей воспользуемся формулами (4) и (5) Простые средние:  – средняя арифметическая – средняя арифметическая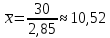 – средняя гармоническая – средняя гармоническая – средняя геометрическая – средняя геометрическая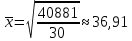 – средняя квадратическая – средняя квадратическаяВзвешенные средние: 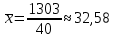 – средняя арифметическая – средняя арифметическая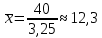 – средняя гармоническая – средняя гармоническая – средняя геометрическая – средняя геометрическая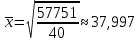 – средняя квадратическая – средняя квадратическаяДля того, чтобы посчитать медиану, нужно посчитать среднюю арифметическую величину, которая рассчитывается из двух смежных величин. Медиана будет равна 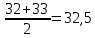 Модой будет вариант с наибольшей частотой. Значит, мода равна 21. Для нахождения дисперсии воспользуемся формулой (11)  Для нахождения среднего квадратического отклонения берем квадратный корень из дисперсии:  Задание 2 Чтобы произвести группировку фирм необходимо посчитать величину интервала. Для этого находим максимальное и минимальное значение, а также считаем количество групп по формуле Стерджесса (1). xmax= 18,4 xmin= 2,5 n = 1 + 3,32*lg30 ≈ 5,9 = 6 Значит, величина интервала по формуле (2) будет равна 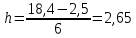 Округляя, получим h = 3 На основе равноинтервальной структурной группировки построим вариационный частотный и кумулятивный ряды распределения. Таблица 2.1 – Вариационный частотный и кумулятивный ряды распределения
 Рис. 3 – частотный ряд распределения  Рис. 4 – кумулятивный ряд распределения Воспользуемся формулами (5) для расчета средних взвешенных показателей: 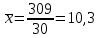 – средняя арифметическая – средняя арифметическая – средняя гармоническая – средняя гармоническая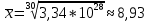 – средняя геометрическая – средняя геометрическая – средняя квадратическая – средняя квадратическаяЛинейное отклонение считаем по формуле (10):  Медиану и моду считаем по формулам (6), (7) соответственно:   Среднее квадратическое отклонение считаем по формуле (14): 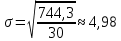 Дисперсию считаем по формуле (12):  Коэффициент вариации, линейный коэффициент вариации и коэффициент осцилляции считаем по формулам (15), (16), (17):    | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
