Расчетно-графическая работа соц-эконом прогноз. Содержание Задания Теоретическая часть Расчетная часть Приложение а приложение б приложение в приложение г список используемой литературы Задания Задание 1
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
Задание 3 На основе таблицы построим график линейной трендовой модели. 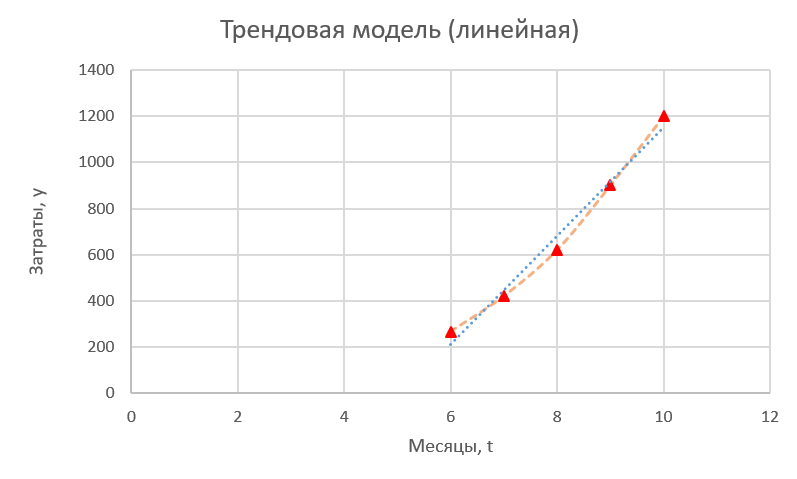 Рис. 5 – Линейная трендовая модель Далее определяем коэффициенты уравнения (18) 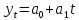 Система нормальных уравнений имеет вид (19): 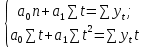 n = 5, 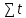 = 40, = 40, 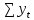 = 3406, = 3406, 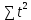 = 330, = 330, 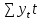 = 29596 = 29596Матрица коэффициентов и вектор свободных членов будет иметь вид: 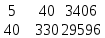 Находим решение системы уравнений:  Записываем новое уравнение 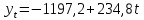 Вычисляем новые значения Y Таблица 3.1 – Новые значения Y для первой модели
Далее выполняем проверку адекватности и точности модели. Проверка на точность. Считаем среднеквадратическое отклонение по формуле (27): 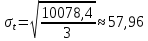 Средняя относительная ошибка аппроксимации по формуле (28): 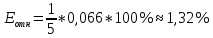 Коэффициент сходимости по формуле (29):  Коэффициент детерминации по формуле (30): 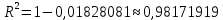 Проверка на адекватность. Проверка случайности колебаний уровней остаточной последовательности. Располагая величины Etв порядке возрастания получаем, что Em = -16. Сравним это значения с последовательностью Etи проставим знаки. Таблица 3.2 – Сравнение с Et для первой модели
Получилось, что максимальная серия Kmax = 2, всего серий v = 3. Проверяем условия (21): Kmax < 5,6 v > 1,04 Проверка выполнилась. Проверка соответствия распределения случайной компоненты нормальному закону распределения Определяем выборочные характеристики асимметрии и эксцесса и их ошибки по формулам (22): 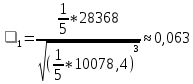 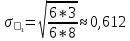 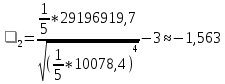 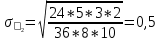 Проверяем условия (23):  < 0,92 < 0,92| 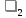 + 1|<0,75 + 1|<0,75Проверка выполнилась. Проверка равенства математического ожидания случайной компоненты нулю Воспользуемся формулой (25): 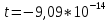 Расчетное значение tменьше табличного значения. Проверка выполнилась. Воспользуемся формулой (26): 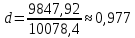 Расчетное значение критерия d больше верхнего табличного значения. Проверка выполнилась. Все указанные четыре проверки свойств остаточной последовательности дают положительный результат, значит модель признается адекватной. Теперь на основе таблицы построим график полиноминальной трендовой модели. 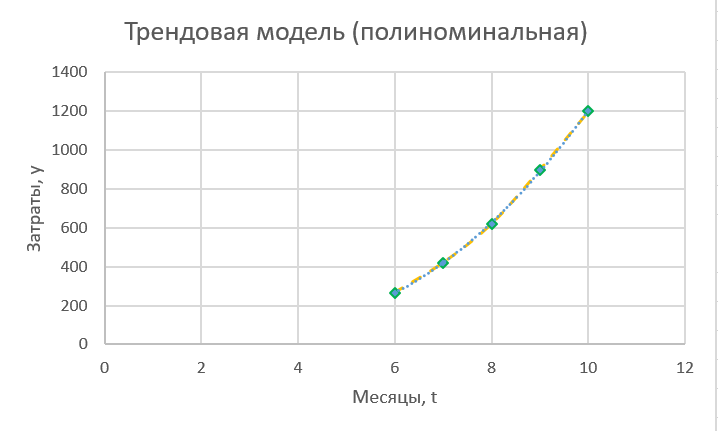 Рис. 6 – Полиноминальная трендовая модель Далее определяем коэффициенты уравнения (18) 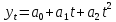 Система нормальных уравнений имеет вид: 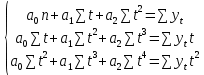 n = 5, 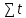 = 40, = 40, 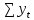 = 3406, = 3406, 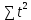 = 330, = 330, 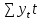 = 29596, = 29596, 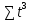 = 2800, = 2800, 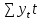 = 29596, = 29596, 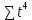 = 24354, = 24354, 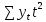 = 262736 = 262736Матрица коэффициентов и вектор свободных членов будет иметь вид: 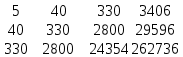 Находим решение системы уравнений: 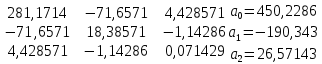 Записываем новое уравнение 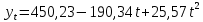 Вычисляем новые значения Y Таблица 3.3 – Новые значения Y для второй модели
Далее выполняем проверку адекватности и точности модели. Проверка на точность. Считаем среднеквадратическое отклонение по формуле (27): 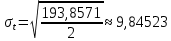 Средняя относительная ошибка аппроксимации по формуле (28): 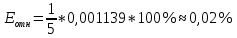 Коэффициент сходимости по формуле (29):  Коэффициент детерминации по формуле (30): 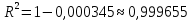 Проверка на адекватность. Проверка случайности колебаний уровней остаточной последовательности. Располагая величины Etв порядке возрастания получаем, что Em = 0,22. Сравним это значения с последовательностью Etи проставим знаки. Таблица 3.4 – Сравнение с Et для второй модели
Получилось, что максимальная серия Kmax = 1, всего серий v = 4. Проверяем условия (21): Kmax < 5,6 v > 1,04 Проверка выполнилась. Проверка соответствия распределения случайной компоненты нормальному закону распределения Определяем выборочные характеристики асимметрии и эксцесса и их ошибки по формулам (22): 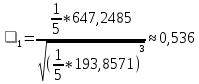 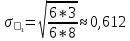 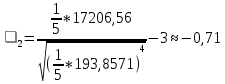 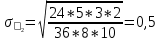 Проверяем условия (23):  <0,92 <0,92| 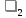 + 1|<0,75 + 1|<0,75Проверка выполнилась. Проверка равенства математического ожидания случайной компоненты нулю Воспользуемся формулой (25): 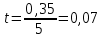 Расчетное значение tменьше табличного значения. Проверка выполнилась. Проверка независимости значений уровней случайной компоненты Воспользуемся формулой (26): 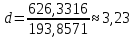 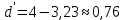 Расчетное значение критерия d больше верхнего табличного значения. Проверка выполнилась. Все указанные четыре проверки свойств остаточной последовательности дают положительный результат, значит модель признается адекватной. Наиболее точная получилась вторая модель. Прогноз на t = 4: 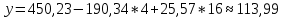 Прогноз на t = 14: 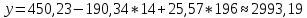 Задание 4 Пользуясь формулами (31), (32) рассчитываем недостающие данные в таблице. Таблица 4.1 – Результат расчетов недостающих данных в таблице
Рассчитываем матрицу коэффициентов прямых затрат по формуле (34): A = 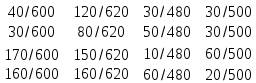 A = 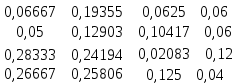 Матрица полных затрат равна обратной матрице B = (E-A)-1 Рассчитываем матрицу (E-A): (E-A) =  – – 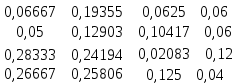 = = 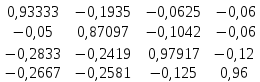 Значит, матрица B будет равна: B =  Матрица косвенных затрат будет равна произведению A*A: A(1) = 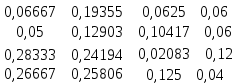 * * 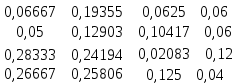 = = 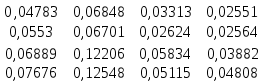 Существование решения гарантированно, т.к. матрица (Е-А) неотрицательно обратима, т.е. существует обратная матрица B>0. Увеличим ассортимент конечного продукта 1-на 5%, 3-на 10%, 4-на 15% Таблица 4.2 – Увеличение ассортимента конечного продукта
Объемы валовой продукции рассчитаем по формуле (38): X =  * * 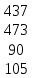 = = 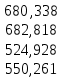 Формулу для межотраслевых потоков в плановом периоде выразим из формулы (34): 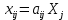 Таблица 4.3 – Расчет межотраслевых потоков
Условно-чистую продукцию каждой отрасли в плановом периоде выразим из формулы (31):  Таблица 4.4 – Расчет условно-чистой продукции
Таблица 4.5 – Новая производственная программа
4. Приложение А 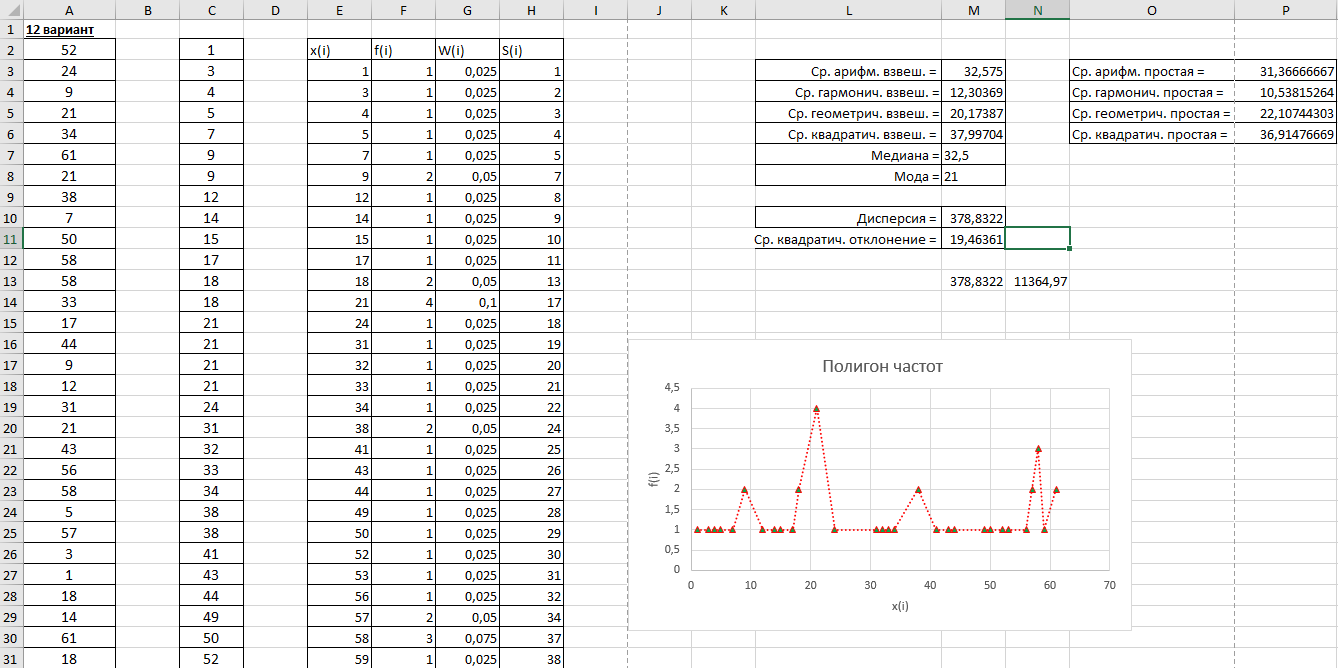 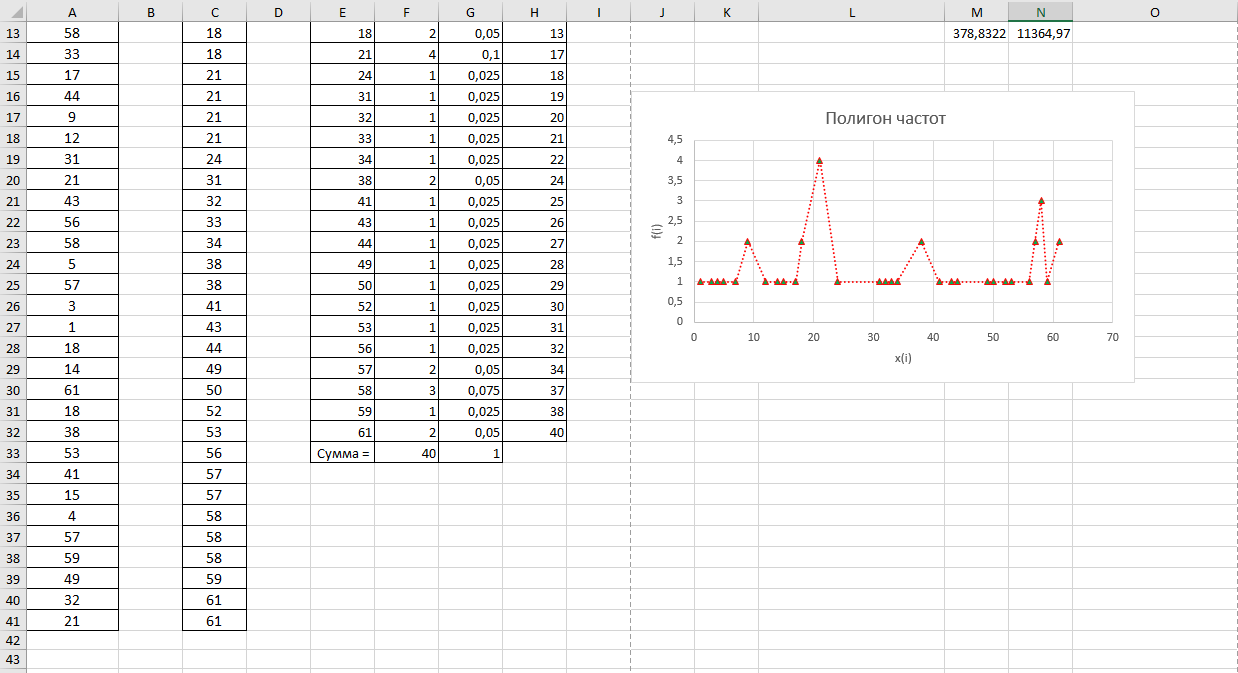 5. Приложение Б 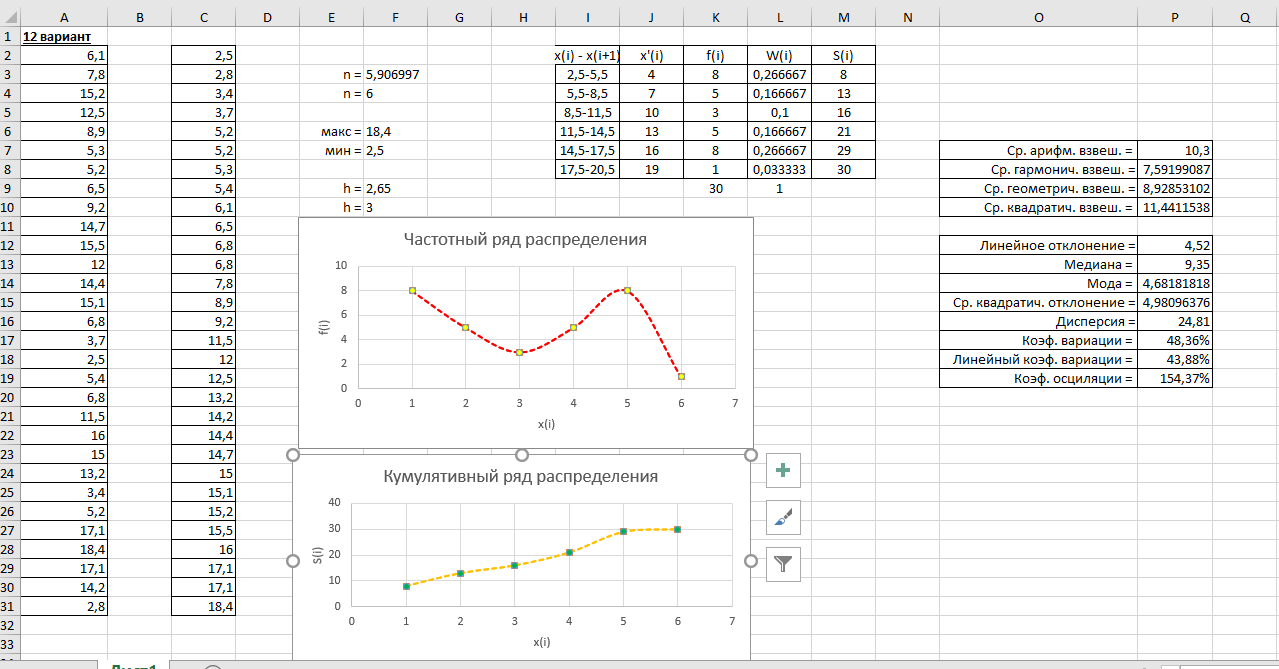 6. Приложение В 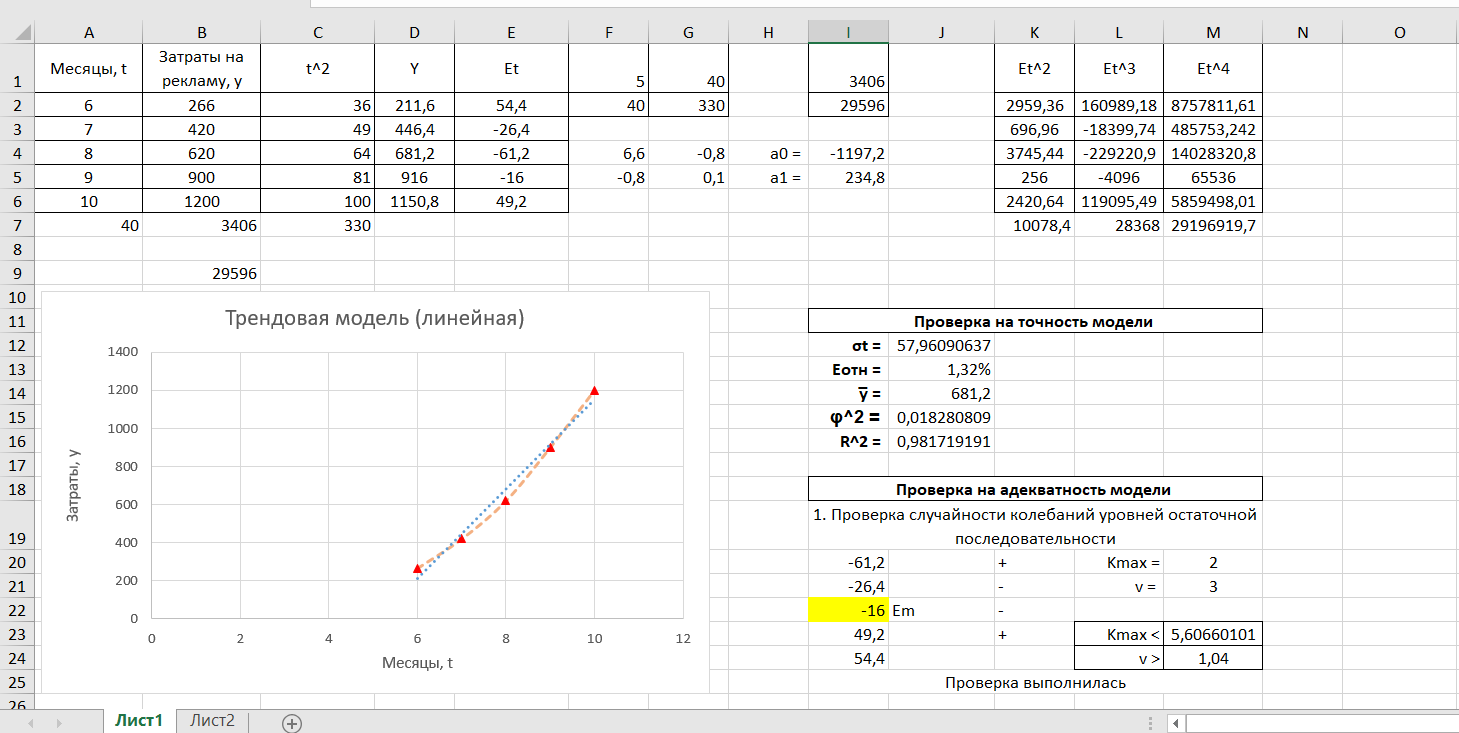  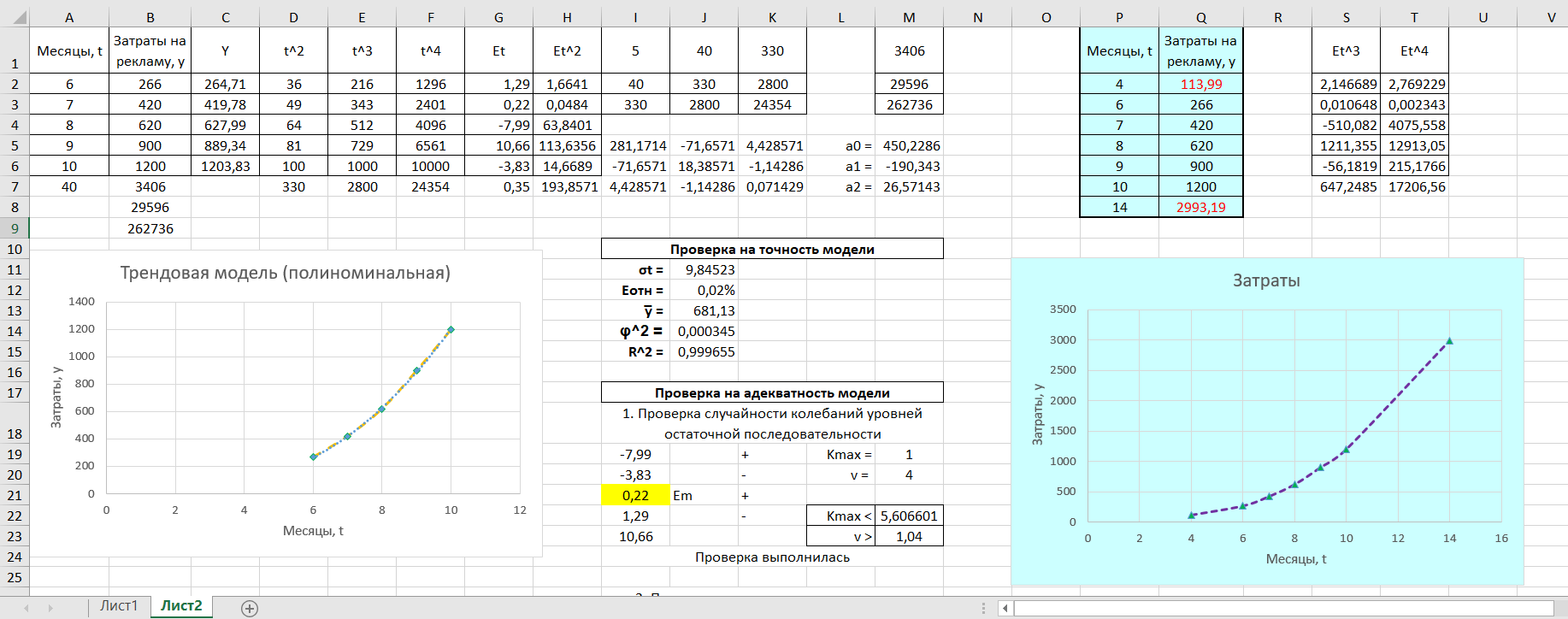  7. Приложение Г 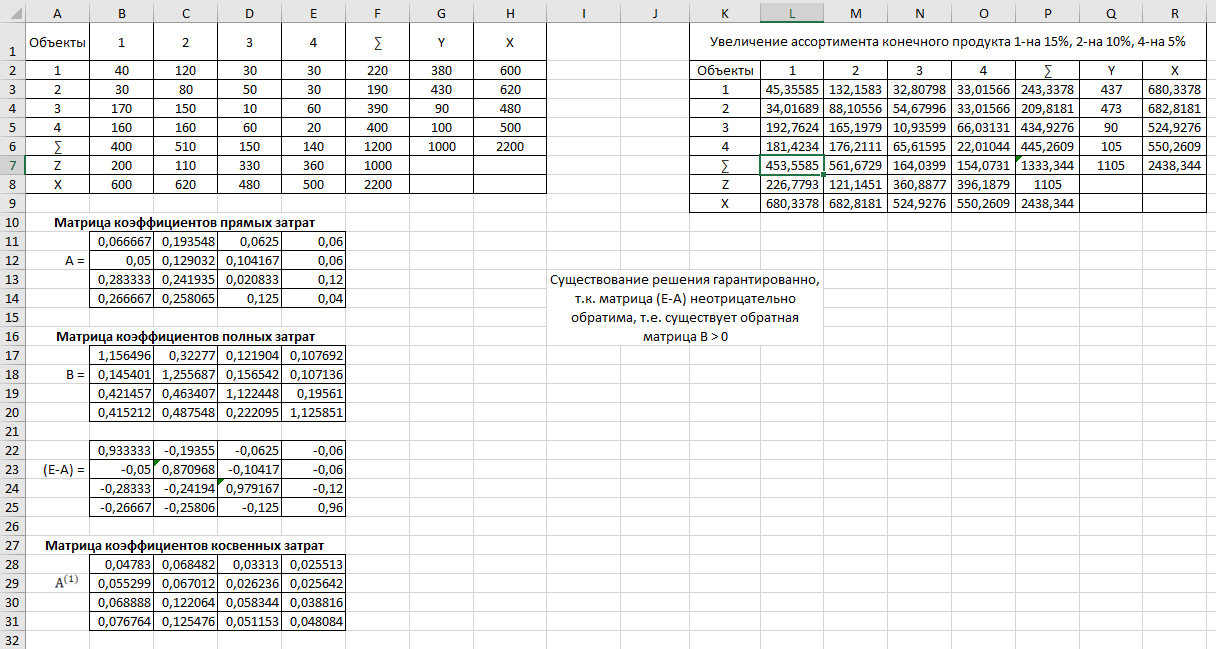 Список используемой литературы 1. Глебова Т.А., Чиркина М.А. Математические модели в экономике: учебное пособие, — Пенза, ПГУАС, 2013. — 137 c. |
