Фалев. Содержит четыре возможных состояния. Обозначим их

• Название: Содержит четыре возможных состояния. Обозначим их
• Дата: 24.03.2023
• Размер: 42.31 Kb.
• Имя файла: Фалев.docx
• Тип: Документы; #1012590

А) Данная система содержит четыре возможных состояния. Обозначим их S_i, i 1, 2, 3, 4 ,

они будут являться вершинами графа и построим граф переходов по матрице

 ^{0 0 1 0} 

^ 4 0 3 0 ^

L ^{ } .

^ 0 3 0 4 ^

 

_ 0 1 1 0 _
Получим: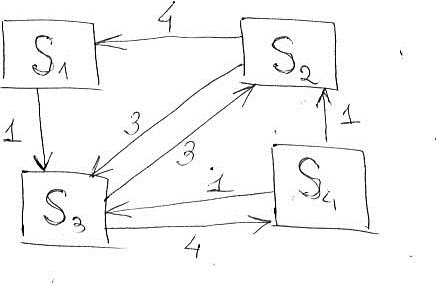

Б) Пусть

^pi^t

- вероятность того, что система находится в состоянии S_iв момент

времени t, i 1, 2, 3, 4 .

Составим систему уравнений Колмогорова по следующим правилам: слева от знака

равенства стоит производная от вероятности

p_i(t) -

^pi(t) , справа в уравнении стоит

dt

сумма произведений вероятностей всех переходов, входящих (входящие стрелки) в

состояние

S_iсистемы, на интенсивности состояний, из которых эти потоки исходят,

минус вероятность

p_i(t) , рассматриваемого состояния

S_i, умноженная на суммарную

интенсивность переходов, выводящих (выходящие стрелки) из данного состояния S_i

систему. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний

n

СМО равна единице: _∑ p_i(t)  1

i1

Получаем систему:

^p1 ^t ^{ p2} ^t ^{ p3} ^t ^{ p4} ^t ^{ 1 .}

Составляем остальные уравнения по графу переходов:

^{dp1 t}  4 p(t) 1p(t),

_dt 2 1

^{dp2 t  3 p(t) 1p}^t ^{ 7 p(t),}

_dt 3 4 2

^{dp3 t  1p(t)  3 p}^t ^1p^t ^{ 7 p(t),}

_dt 1 2 4 3

^dp4 ^t _{ 4 p}

^t ^{ 2 p(t).}

_dt 3 4

Система для определения вероятностей различных состояний.

^{ dp1 t}  4 p(t) 1p(t),

 _dt 2 1


^{ dp2 t}  3 p(t) 1p


^t ^{ 7 p(t),}


^ dt

3 4 2

^{ dp3 t}  1p(t)  3 p


^t ^1p

^t ^{ 7 p(t),}



_ dt

1 2 4 3

^{ dp4} ^t _{ 4 p}


^t ^{ 2 p(t),}


^ _dt 3 4

^{ p1} ^t ^{ p2} ^t ^{ p3} ^t ^{ p4} ^t ^{ 1.}




Так как предельные вероятности постоянные, заменяем производные нулями

(производная от константы – нуль) и приходим к системе алгебраических уравнений:


^{4 p2  p1  0,}

_3 p₃  p₄  7 p₂  0,

^ p 3 p p 7 p

 0,

^ 1 2 4 3

^4 p 2 p 0,

_ 3 4

_ p₁  p₂  p₃  p₄  1.
В) Решим эту систему уравнений.



 ^{p1  4 p2 ,}

_3 p₃  2 p₃  7 p₂  0,

^4 p 3 p 2 p 7 p 0,

^ 2 2 3 3

^ p 2 p,

_ 4 3

_4 p₂  p₂  p₃  2 p₃  1.



 ^{p1  4 p2 ,}

_5 p₃  7 p₂  0,


^7 p

 <sub>p

2</sub>  5 p₃

 2 p,

 0,

_ 4 3

_5 p₂  3 p₃  1.

 ^{p1  4 p2 ,}



^7 p 5 p 0, | *5

2 3

^ p 2 p,

_ 4 3

^_5 p₂  3 p₃  1. | *7

 <sup>p1  4 p2 ,

</sup>35 p 25 p 0,

^ 2 3


p


_{ 4}  2 p₃ ,

^_35 p₂  21p₃  7.

 ^{p1  4 p2 ,}


^7 p

 <sub>p

2</sub>  5 p₃ ,

 2 p,

_ 4 3

^_46 p₃  7.

 ^{p1  4 p2 ,}

 ₇

^7 p₂  5 ,



 46



^ p 2 ⁷ ,

^{ 4} 46

^ p ⁷ .

^{ 3} 46


^ p ¹⁰ ,

^{ 1} 23

^ p ⁵ ,

^{ 2} 46

 ₇


4
^ p ,

^ 23

 ₇



^ p₃  ₄₆ .

Предельная вероятность каждого состояния:



^ p ¹⁰ ,

^{ 1} 23

^ p ⁵ ,

^{ 2} 46

 ₇


3
^ p ,

^ 46

 ₇



^ p₄  ₂₃ .