Сопротивление материалов, Б. Козионов Условие задачи
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Сопротивление материалов, Б.Козионов   Условие задачи Разделим брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние нагрузки. Мысленно рассечем брус в пределах первого участка и отбросим верхнюю часть бруса. Действие отброшенной части заменим продольной силой N1, которая уравновешивается силой Р1: N1 = Р1 = 15 кН. Аналогично, в пределах второго участка отбросим верхнюю часть бруса и рассмотрим оставшуюся часть бруса с действующей силой Р1, которая уравновешивается силой N2: N2 = Р1 = 0кН. Продольная сила на третьем участке N3, уравновешивается внешними силами Р1 и Р2 и равна их алгебраической сумме: N3 = Р1 +Р2 =15 кН + 25кН = 40 кН. В пределах каждого участка нагружения продольная сила постоянна и, поэтому на эпюре изобразится линией, параллельной оси бруса. Для построения эпюры продольных сил проводим линию, параллельную оси бруса. С левой стороны от нее откладываем значение продольной силы, вызванной сжатием (т.е. отрицательные значения продольной силы), а с правой стороны от нее откладываем значение продольной силы, вызванной растяжением (т.е. положительные значения продольной силы). В пределах участка III брус сжат, а в пределах участков I – II брус растянут. Определение величины напряжений и построение эпюры напряжений. Для определения напряжений в поперечных сечениях бруса необходимо значение продольной силы разделить на площади соответствующих сечений: σ = Площадь поперечного сечения бруса первого участка: 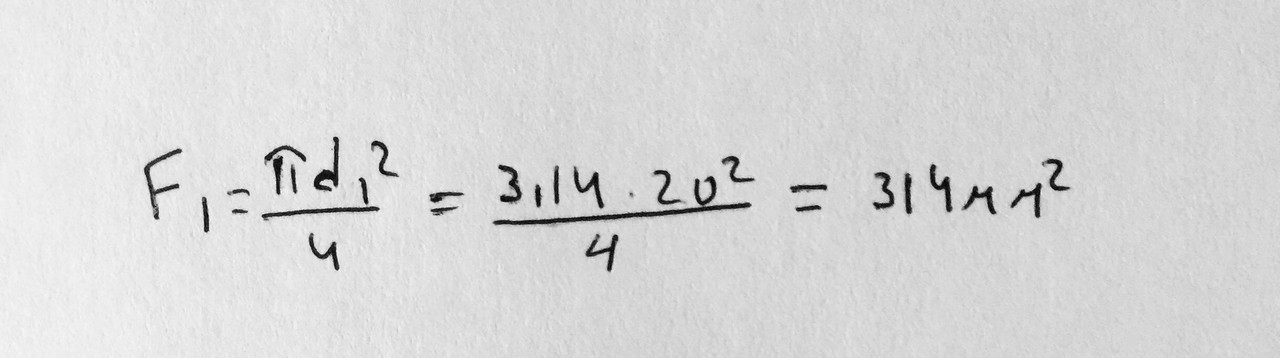 Площадь поперечного сечения бруса на участках II и III:  Находим напряжения на участках бруса:.  По полученным данным строим эпюру нормальных напряжений. Для построения эпюры напряжений проводим линию, параллельную оси бруса. С левой стороны от нее откладываем отрицательные значения напряжений, а с правой - положительные значения напряжений. Для построения эпюры определим перемещения характерных сечений бруса B - B, C - C, D – D. Перемещение сечения А-А равно нулю, т.к. это сечение крепления бруса. Сечение В –В будет перемещаться вверх, поскольку верхняя часть бруса сжимается:  Перемещение сечения С-С является алгебраической суммой перемещения сечения В-В и удлинения части бруса В-С длиной l = 9м :  Перемещение сечения D - D является алгебраической суммой перемещения сечения C-C и удлинения части бруса С – В длиной l = 3м:  Полное удлинение бруса будет равно перемещению сечения D – D, т.е.  Для построения эпюры перемещений сечений бруса откладываем в определенном масштабе на эпюре значения ∆ l b, ∆ l с, ∆ l d , и соединяем полученные точки прямыми линиями. Проверка прочности бруса. Наибольшие действующие напряжения будут на участке I : σmax = σ2 , σ3=63.8 Н/мм2. Сравним их с допускаемыми: σmax = σ2 = 63.8 Н/мм2 ≤ [σ] = 160 Н/мм2. Прочность бруса соблюдается. |
