Составление программ для машины Тьюринга
 Скачать 173.02 Kb. Скачать 173.02 Kb.
|
|
Практическое занятие №4 Тема: Составление программ для машины Тьюринга Цель: организовать деятельность по формулированию понятия "алгоритм” и применению алгоритма в разных ситуациях. Ход занятия Краткие теоретические сведения. Рассмотрим работу Машины Тьюринга. Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты. Таким образом Машина Тьюринга формально описывается набором двух алфавитов: A={a1, a2, a3, …, an} — внешний алфавит, служит для записи исходных данных Q={q1, q2, q3,…, qm} — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.  Машина Тьюринга Каждая ячейка ленты может содержать символ из внешнего алфавита A = {a0,a1,…,an} (В нашем случае A={0, 1}) Допустимые действия Машины Тьюринга таковы: 1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается) 2) сместиться в соседнюю ячейку 3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = {q0,q1,…,qm}. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу. В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей · символ из алфавита A · направление перемещения: «>» (вправо), «<» (влево) или «.» (на месте) · новое состояние автомата  В приведенной выше таблице алфавит A ={0, 1, _} (содержит 3 символа), а внутренний алфавит Q={q1, q2, q3, q4, q0}, q0 — состояние, заставляющее каретку остановиться. Рассмотрим несколько задач решением. Скачать машину Тьюринга Вы можете на сайте в разделе СКАЧАТЬ. Задача 1. Пусть A={0, 1, _}. На ленте в ячейках находятся символы из алфавита в следующем порядке 0011011. каретка находится над первым символом. Необходимо составить программу, которая заменит 0 на 1, 1 на 0 и вернет каретку в первоначальное положение. 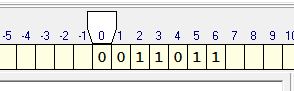 Теперь определимся с состояниями каретки. Я называю их — «желания каретки что-то сделать». q1) Каретка должна пойти вправо: если видит 0 меняет его на 1 и остается в состоянии q1, если видит 1 — меняет его на 0 и остается в состоянии q1, если видит _ — ворачивается назад на 1 ячейку «желает что-то другое», т.е переходит в состояние q2. Запишем наши рассуждения в таблицу исполнителя. Синтаксис смотрите в справке к программе) 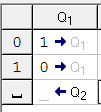 q2) Теперь опишем «желание каретки» q2. Мы должны вернуться в первоначальное положение. Для этого: если видим 1 оставляем ее и остаемся в состоянии q2 (с тем же желанием дойти до конца ряда символов); если видим 0 — оставляем его и продолжаем двигаться влево в состоянии q2; видим _ — сдвигается вправо на 1 ячейку. Вот вы оказались там, где требуется в условии задачи. переходим в состояние q0. 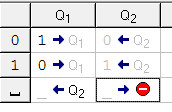 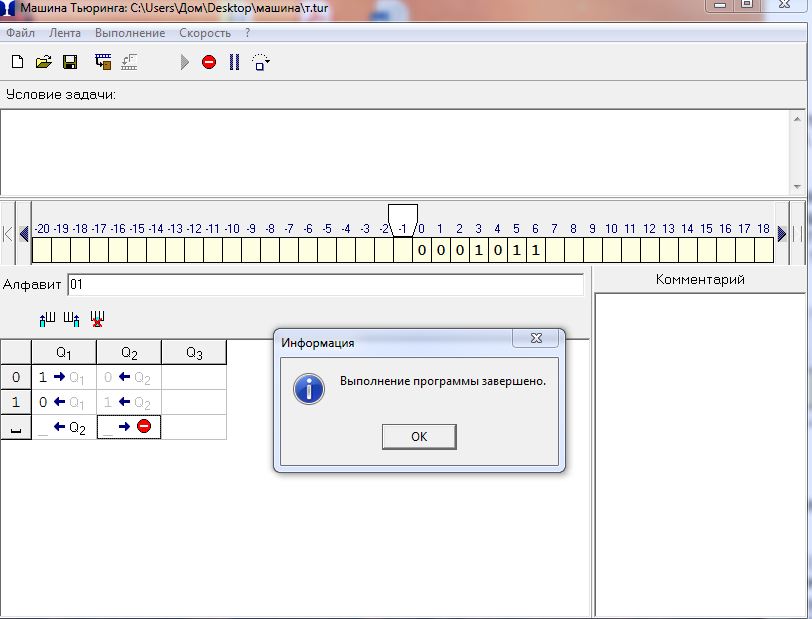 Задача 2. Дано: конечная последовательность 0 и 1 (001101011101). Необходимо выписать их после данной последовательности, через пустую ячейку, а в данной последовательности заменить их на 0. Например: Из 001101011101 получим 000000000000 1111111. Как видите, семь единиц записались после данной последовательности, а на их местах стоят нолики. Приступим к рассуждениям. Определим, какие состояния необходимы каретке и сколько. q1) увидел 1 — исправь на нолик и перейди в другое состояние q2 (новое состояние вводится, чтобы каретка не поменяла на нули все единицы за один проход) q2) ничего не менять, двигаться к концу последовательности q3) как только каретка увидела пустую ячейку, она делает шаг вправо и рисует единичку, если она видит единичку — то движется дальше, чтобы подписать символ в конце. Как только нарисовал единицу, переходим в состояние q4 q4) проходим по написанным единицам, ничего не меняя. Как только доходим до пустой ячейки, разделяющей последовательность от единиц, переходим с новое состояние q5 q5) в этом состоянии идем начало последовательности, ничего не меняя. Доходим до пустой ячейки, разворачиваемся и переходим в состояние q1 Состояние q0 каретка примет в том случае, когда она пройдет в состоянии q1 до конца данной последовательности и встретит пустую ячейку. Получим такую программу: 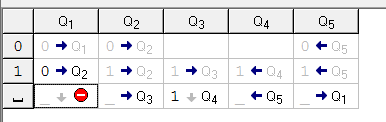 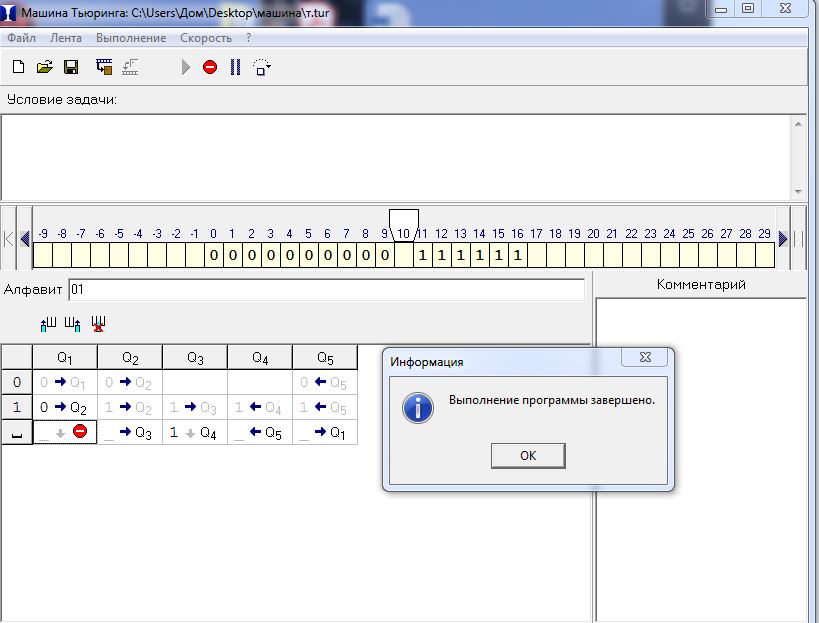 ВЫВОД: Составил программы для машины Тьюринга. Разобрался как перемещается: «>» (вправо), «<» (влево) или «.» (на месте). |
