ЛАБ.РАБОТА 1-5. Лаб. работа 1-5. Соударение шаров
 Скачать 54.3 Kb. Скачать 54.3 Kb.
|
|
Омский государственный технический университет Кафедра физики Отчёт по лабораторной работе №1-5 СОУДАРЕНИЕ ШАРОВ Выполнил(а): студент группы _____________________ ____________________________________ Проверил(а): ________________________ ____________________________________ Дата сдачи отчета:_____________________ Лабораторная работа № 1-5 СОУДАРЕНИЕ ШАРОВ Цель работы: изучение взаимодействия шаров при ударе, определение коэффициента восстановления скорости при ударе. Приборы и принадлежности: лабораторная установка «Соударение шаров», электронный блок. Краткая теория Центральным ударом называется… Абсолютно упругим ударом называется… При абсолютно упругом ударе выполняются… Абсолютно неупругим ударом называется… При абсолютно неупругом ударе выполняется… Коэффициентом восстановления скорости называется величина, равная…… Теоретическое значение коэффициента восстановления скорости можно вычислить по формуле: (1) В формуле (1): V1 и V2 – … U1 и U2 –… Коэффициент восстановления скорости k =… для абсолютно упругого удара и k =… для абсолютно неупругого удара. В лабораторной работе удар тел исследуется на установке «Соударение шаров» (рис. 1). Измеряются углы отклонения нитей, на которые подвешены шары, от вертикали до и после удара. С помощью закона……………………………………..эти углы можно связать со скоростями движения шаров. 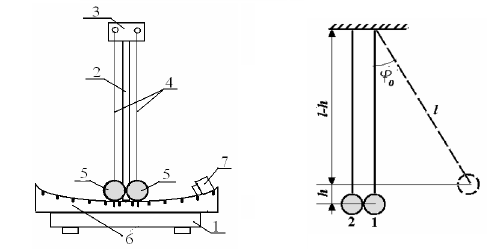 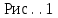 Рис.1 Расчетная формула для коэффициента восстановления скорости имеет вид: (2) В этой формуле: φ0 – φ1 – ... φ2 – … Экспериментальная часть Отклонить шар №1 на заданный угол φ0, измерить углы φ1 и φ2 отклонений шаров №1 и № 2 непосредственно после удара (рис. 1). Опыт проводится 5 раз. Результаты измерений занести в табл. 1. Таблица 1
приборная погрешность измерения углов ∆φприб = град. Студент(ка) гр._______________________________________(указать ФИО) Дата выполнения_______________________Преподаватель________________ Обработка результатов измерений Расчет угла φ1 Вычислить среднее арифметическое значение угла φ1. <φ1> = Вычислить абсолютные отклонения результатов каждого измерения от величины <φ1> Δφ11 = Δφ12 = Δφ13 = Δφ14 = Δφ15 = Вычислить среднеквадратичную погрешность опыта. 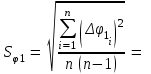 По таблице коэффициентов Стьюдента определить коэффициент Стьюдента tα.n при коэффициенте надежности α = 0,9 и числе измерений n = 5 и вычислить абсолютную случайную погрешность опыта измерения времени. ∆φ1сл = tα.n∙Sφ1 = Вычислить абсолютную погрешность угла φ1. 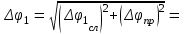 Вычислить относительную погрешность угла φ1: 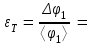 Записать ответ: φ1 = ( ± ) О ε1 = % Расчет угла φ2 Вычислить среднее арифметическое значение угла φ2. <φ2> = Вычислить абсолютные отклонения результатов каждого измерения от величины <φ2>. Δφ21 = Δφ22 = Δφ23 = Δφ24 = Δφ25 = Вычислить среднеквадратичную случайную погрешность опыта. 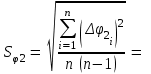 По таблице коэффициентов Стьюдента определить коэффициент Стьюдента tα.n при коэффициенте надежности α = 0,9 и числе измерений n = 5 и вычислить абсолютную случайную погрешность опыта измерения времени. ∆φ2сл = tα.n ·Sφ2 = Вычислить абсолютную погрешность опыта. 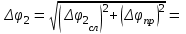 Вычислить относительную погрешность угла φ1: 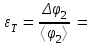 Записать ответ: φ2 = ( ± ) О ε2 = % Рассчитать коэффициент восстановления скорости k по формуле (2), используя средние значения углов отклонения шаров. k= Рассчитать абсолютную погрешность определения коэффициента восстановления скорости ∆k по методике косвенных воспроизводимых измерений (∆φО = ∆φпр).  Рассчитать относительную погрешность опыта.  Записать ответ: k = ( ± ) ε = % Выводы 1. Изучен метод определения………………………………………… при ударе двух … ………..шаров на установке…………………….. 2. Измерены значения………………………………………………… 3. Рассчитано значение………………………………………………… k = ( ± ) ε = % 4. Исследуемый удар является… , так как значение…………………………………………………… |
