Стартовая диагностика. Стартовая диагностика

• Название: Стартовая диагностика
• Дата: 10.04.2022
• Размер: 275.84 Kb.
• Имя файла: Стартовая диагностика.docx
• Тип: Документы; #458193

Стартовая диагностика

1. 
   В кодировке Windows-1251 каждый символ кодируется 8 бит.
   Вова хотел написать текст (в нём нет лишних пробелов):
   «Скользя по утреннему снегу,
   Друг милый, предадимся бегу
   Нетерпеливого коня
   И навестим поля пустые…»
   
   
   

Одно из слов ученик написал два раза подряд через пробел. При этом размер написанного предложения в данной кодировке оказался на 10 байт больше, чем размер нужного предложения. Напишите в ответе лишнее слово.


Ответ: ___________________________.

2. 
   У исполнителя Вычислитель две команды, которым присвоены номера:
   1. умножь на b
   2. прибавь 1
   (b – неизвестное натуральное число)
   Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 1.
   Известно, что программа 21212 переводит число 1 в число 56.
   Определите значение b.
   Ответ: ___________________________
   

3. 
   Ниже приведена программа, записанная на пяти языках программирования.
   

С++	Python	Паскаль
#include using namespace std; int main() { int s, k, A; cin >> s; cin >> k; cin >> A; if s < A || k < 6 cout << "ДА"; else cout << "НЕТ"; return 0; }	s = int(input()) k = int(input()) A = int(input()) if s < A or k < 6: print("ДА") else: print("НЕТ")	var s, k, A: integer; begin readln(s); readln(k); readln(A); if (s < A) or (k < 6) then writeln(′ДА′) else writeln(′НЕТ′) end.
Алгоритмический язык	Бейсик
алг нач цел s, k, A ввод s ввод k ввод A если s < A или k < 6 то вывод "ДА" иначе вывод "НЕТ" все кон	DIM k, s, A AS INTEGER INPUT s INPUT k INPUT A IF (s < A) OR (k < 6) THEN PRINT ′ДА′ ELSE PRINT ′НЕТ′ END IF

Было проведено 9 запусков программы, при которых в качестве значений
переменных s и k вводились следующие пары чисел:
(10, 12); (8, 10); (16, 2); (5, 15); (2, 9); (–10, 7); (–10, 12); (4, 1); (20, 8).
Укажите минимальное целое значение параметра А, при котором для
указанных входных данных программа напечатает «ДА» пять раз.
Ответ: ___________________________.

4. 
   Значение арифметического выражения 9⁹ + 3¹⁵ - 23 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
   
5. 
   Для хранения в информационной системе документы сканируются с разрешением 300 ppi. При этом используется палитра, содержащая  2²⁴= 16777216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 12 Мбайт. В целях экономии было решено перейти на разрешение 200 ppi и уменьшить количество цветов в палитре до 512. Определите средний размер документа, отсканированного с изменёнными параметрами. Ответ запишите в Мб.
   
6. 
   На рисунке справа схема путей Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих путей (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Укажите кратчайший путь из пункта А в пункт Ж. В ответе перечислите все населённые пункты, через которые проходит путь, буквы в ответе запишите заглавные на русской раскладке клавиатуры.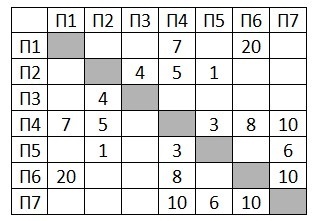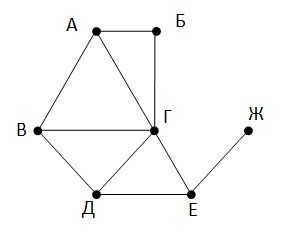
   

7. 
   Ниже представлены два фрагмента таблиц из базы данных о жителях микрорайона. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведённых данных, у скольких детей на момент их рождения матерям было больше 20 полных лет. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц.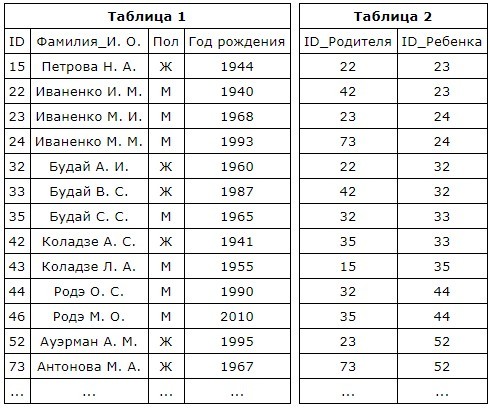
   

8. 
   Руслан составляет 5-буквенные коды из букв Р, У, С, Л, А, Н. Каждая
   допустимая гласная буква может входить в код не более одного раза.
   Сколько кодов может составить Руслан?
   

9. 
   Каждый объект, зарегистрированный в информационной системе, получает уникальный код из 9 символов, каждый из которых может быть одной из 26 заглавных или строчных латинских букв. Для представления кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Кроме того, для каждого объекта в системе выделен одинаковый объём памяти для хранения содержательной информации. Для хранения данных (код и содержательная информация) о 50 объектах потребовалось 2500 байт. Сколько байтов выделено для хранения содержательной информации об одном объекте?
   В ответе запишите только целое число – количество байтов.
   

10. 
    Алгоритм вычисления значения функции F(n), где n – целое неотрицательное
    число, задан следующими соотношениями:
    F(0) = 0;
    F(n) = F(n/2), если n > 0 и при этом n чётно;
    F(n) = 1 + F(n – 1), если n нечётно.
    Сколько существует таких чисел n, что 1 ≤ n ≤ 1000 и F(n) = 3?
    Ответ: ___________________________
    

11. 
    На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт И?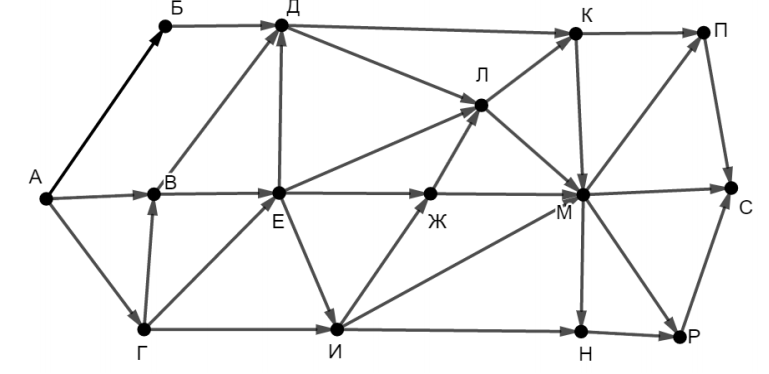
    

Ответ: ___________________________

12. 
    
    

13. 
    Исполнитель Март21 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
    1. Прибавить 1
    2. Умножить на 2
    3. Умножить на 3
    Сколько существует программ, для которых при исходном числе 4 результатом является число 38 и при этом траектория вычислений содержит число 11 и не содержит число 18?
    

14. 
    (19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: а) добавить в любую кучу один камень; б) добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда суммарное количество камней в двух кучах становится не менее 62. В начальный момент в первой куче было 14 камней, а во второй – S камней, 1 ≤ S ≤ 47. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
    

15. 
    (20)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в любую кучу один камень; б) добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда суммарное количество камней в двух кучах становится не менее 62. В начальный момент в первой куче было 14 камней, а во второй – S камней, 1 ≤ S ≤ 47. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: − Петя не может выиграть за один ход; − Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе через пробел в порядке возрастания.
    

16. 
    (21)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в любую кучу один камень; б) добавить в любую кучу столько камней, сколько их в данный момент в другой куче. Игра завершается в тот момент, когда суммарное количество камней в двух кучах становится не менее 62. В начальный момент в первой куче было 14 камней, а во второй – S камней, 1 ≤ S ≤ 47. Найдите значение S, при котором одновременно выполняются два условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
    

«Методика подготовки обучающихся к олимпиадам по информатике и ИКТ»