Пример решения задачи по теме «Статика»
Стержень массой 9 кг и длиной 1 м лежит на двух опорах. Одна из них подпирает левый конец стержня, а другая находится на расстоянии 10 см от правого конца. С какой силой действует на стержень каждая из опор?
Дано:
m = 1 кг
L = 1 м
s = 0,1 м
|
Решение:
А) Требование задачи – найти силу, действующую на стержень со стороны каждой опоры, т.е. требуется найти силы реакции опоры N1 и N2.
Б) По условию задачи стержень покоится, т.е. в равновесии. Для решения задачи можем применить условие равновесия (правило моментов): ΣМ= 0.
|
N1 - ? N2 - ?
|
В ) Для вычисления моментов сил потребуется знать плечи сил и направление вращения стержня под действием этих сил, поэтому не обойтись без рисунка. ) Для вычисления моментов сил потребуется знать плечи сил и направление вращения стержня под действием этих сил, поэтому не обойтись без рисунка.
Рисунок:
А) укажем силы, действующие на тело,
Б) обозначим расстояния, указанные в условии – они помогут определить плечи сил. Для удобства концы стержня обозначим буквами А и В, середину стержня С, вторую опору D.
В) Ось вращения.
С тержень может вращаться вокруг нескольких осей: ось вращения может проходить через точки А, С, D или В. Значит, требуется выбрать ось вращения. Выберем ось вращения, проходящую через точку А. тержень может вращаться вокруг нескольких осей: ось вращения может проходить через точки А, С, D или В. Значит, требуется выбрать ось вращения. Выберем ось вращения, проходящую через точку А.
Определим плечи сил относительно выбранной оси вращения – точки А.
ℓN1 = 0, т.к. линия действия силы проходит чрез ось вращения;
ℓ N2 = AD
ℓmg = AC
Используя условие задачи, выразим плечи сил через расстояния L и s
ℓ N2 = AD = L – s
ℓmg = AC = 0,5L, т.к. сила тяжести приложена в центре стержня.
Определим моменты сил.
МN2 = – N2·(L – s), т.к. сила N2 вращает стержень вокруг точки А против часовой стрелки.
МN1 = 0
Мmg = mg·0,5L, т.к. сила тяжести вращает стержень вокруг точки А по часовой стрелке.
Запишем правило моментов ΣМА = 0
0 – N2·(L – s) + 0,5mgL = 0
Откуда N2·(L – s) = 0,5mgL
и окончательно N2 = 0,5mgL / (L – s)
Расчёт N2 = 0,5 · 9 кг · 10 м/с2 · 1 м/ (1 м – 0,1 м) = 50 Н
Теперь необходимо вычислить силу N1. Возможны два способа.
I способ найти N1.Т. к. стержень неподвижен, то должно выполняться и другое условие равновесия 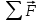 =0 =0
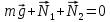
Спроецируем силы на вертикальную ось oY, получим –mg + N1 + N2 = 0
Откуда выразим N1 = mg – N2
N1 = 9 кг · 10 м/с2 – 50 Н = 40 Н.
II способ. Так как стержень в равновесии, то условие равновесия справедливо относительно любой оси вращения.
Выберем ось вращения в точке D, определим плечи и моменты сил относительно точки D.
ℓN1 = AD = L – s
ℓ N2 = 0, т.к. линия действия силы проходит чрез ось вращения
ℓmg = CD = 0,5L – s
М N1 = – N1·(L – s), т.к. сила N1 вращает стержень вокруг точки D по часовой стрелке N1 = – N1·(L – s), т.к. сила N1 вращает стержень вокруг точки D по часовой стрелке
МN2 = 0
Мmg = + mg·(0,5L – s), т.к. сила тяжести вращает стержень вокруг точки D против часовой стрелки.
Правило моментов относительно точки D
mg·(0,5L – s) – N1·(L – s) + 0 = 0
После преобразований N1 = mg·(0,5L – s) / (L – s)
Расчёт N1 = 90 Н·0,4 м / 0,9 м = 40 Н.
Оба способа дали одинаковый ответ.
| |
 Скачать 43.1 Kb.
Скачать 43.1 Kb.
 ) Для вычисления моментов сил потребуется знать плечи сил и направление вращения стержня под действием этих сил, поэтому не обойтись без рисунка.
) Для вычисления моментов сил потребуется знать плечи сил и направление вращения стержня под действием этих сил, поэтому не обойтись без рисунка. тержень может вращаться вокруг нескольких осей: ось вращения может проходить через точки А, С, D или В. Значит, требуется выбрать ось вращения. Выберем ось вращения, проходящую через точку А.
тержень может вращаться вокруг нескольких осей: ось вращения может проходить через точки А, С, D или В. Значит, требуется выбрать ось вращения. Выберем ось вращения, проходящую через точку А.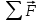 =0
=0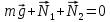
 N1 = – N1·(L – s), т.к. сила N1 вращает стержень вокруг точки D по часовой стрелке
N1 = – N1·(L – s), т.к. сила N1 вращает стержень вокруг точки D по часовой стрелке