задание 1. Статистические методы сбора и обработки данных
 Скачать 381.38 Kb. Скачать 381.38 Kb.
|
|
Тема 4. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ Задача 4.1. Установите характер и форму связи между валовым национальным продуктом и экспортом РФ методами приведения параллельных данных, статистических графиков и корреляционно-регрессионного анализа. По полученной регрессионной модели постройте прогноз экспорта РФ на период упреждения 3 шага (года), прогнозные значения ВВП оцените по наиболее адекватной модели тренда. Исходные данные и вспомогательная таблица для расчета параметров уравнения регрессии.
Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. Значения факторного анализа располагаются в возрастающем порядке и отслеживается направление изменения величины результативного признака. Результативный признак обозначается через у (в данном случае экспорт), а факторный признак – через х (в данном случае ВВП). В целом, можно сделать вывод, что при увеличении ВВП возрастает экспорт. В тех случаях, когда возрастание величины факторного признака влечет за собой возрастание величины результативного признака, говорят о возможном наличии прямой корреляционной связи. В графическом методе взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абцисс (ось х) откладываются значения факторного признака, а на оси ординат (ось у) – результативного. Каждое пересечение линий, проводимых через эти оси обозначают точкой. При отсутствии связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее точки будут группироваться вокруг определенной линии. 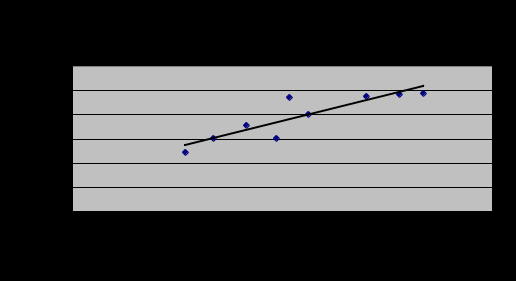 Эмпирическая линия связи по своему виду приближается к прямой линии, это говорит о наличии прямолинейной корреляционной связи между признаками. Наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие параллельных рядов. В таких случаях целесообразнее воспользоваться для установления факта наличия связи статистическими таблицами – корреляционными или групповыми. Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. В первый столбец корреляционной таблицы заносим факторный признак. Для результативного признака необходимо определить величину интервала hy. Для этого воспользуемся формулой Стэрджесса: 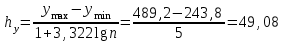 Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного сочетания значения х и у.
ƒх – частота повторения данного варианта значения факторного признака во всей совокупности; ƒу – частота повторения результативного признака во всей совокупности. Частоты в корреляционной таблице расположены по диагонали из левого верхнего угла в правый нижний угол, таким образом наблюдаем прямую корреляционную зависимость между признаками. При рассмотрении корреляционной таблицы важно установить расположение основной части частот. Возможны варианты, когда все клетки корреляционной таблицы окажутся заполненными. Однако это обстоятельство еще не означает, что корреляционная связь между признаками отсутствует. Корреляционная таблица позволяет сжато, компактно изложить материал, поэтому все последующие расчеты можно вести по корреляционной таблице. Получение регрессионной модели происходит в два этапа: - подбор вида функции; - вычисление параметров функции. Чаще всего выбор производится среди следующих функций: y = a0+a1t – линейная функция; y = a ln(x) + b – логарифмическая функция; y = a ebx – экспоненциальная функция. На графиках изображены 3 функции, построенные методом наименьших квадратов по данным, представленным в таблице. 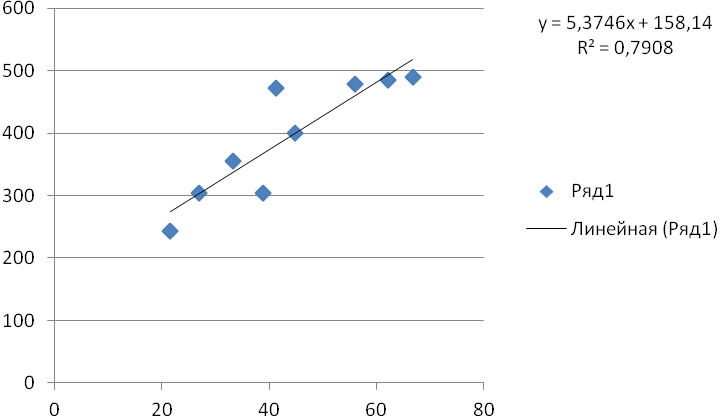 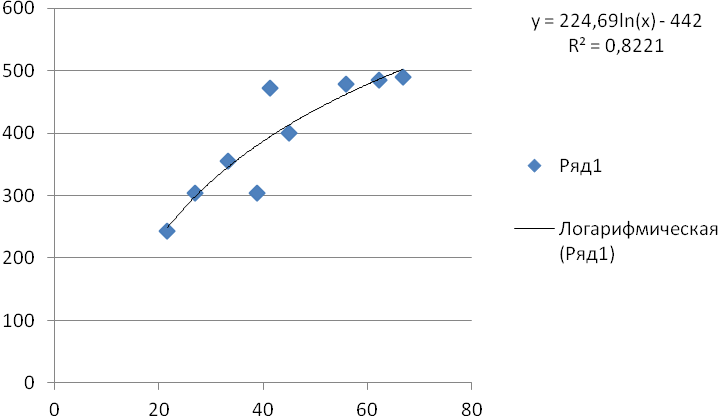 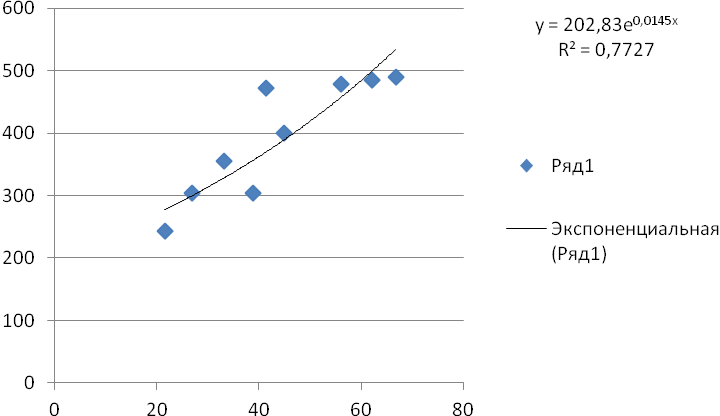 Данные рисунки получены с помощью MS Excel. График регрессионной модели называется трендом. На каждом графике изображена искомая функция, а также еще одна величина, полученная в результате построения тренда. Она обозначена как R2. В статистике эта величина называется коэффикиентом детерминированности. Именно она определяет, насколько удачной является полученная регрессионная модель. Коэффициент детерминированности всега заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели предельно неудачен. Чем ближе R2 к 1, тем удачнеерегрессионная модель. Из трех выбранных моделей наименьшее значение у экспоненциальной, значит она самая неудачная. Наибольшее значение у логарифмической, значит она будет самой удачной. После получения регрессионной математической модели можно прогнозировать процесс путем вычисления. Существует два способа прогнозов по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной, то это называется восстановлением значения. Прогнозирование за пределами экспериментальных данных называется экстраполяцией. Для расчета используем метод линейной экстраполяции. Сущность метода заключается в том, что прогнозные величины определяются на основе среднего прироста (снижения) исследуемого показателя за определенный период времени.
Определив средний темп прироста, рассчитаем прогнозное значение ВВП на 2014,2015,2016 гг. Y2014=66,8+5,65=72,45 Y2015=72,45+5,65=78,1 Y2016=78,1+5,65=83,75 Определив прогнозный ВВП, можно определить прогноз экспорта по логарифмическому уравнению: y=224,69 ln(x) – 442 Y2014=224,69 ln72,45 – 442 = 520,32 Y2015=224,69 ln78,1 – 442 = 537,20 Y2016=224,69 ln83,75 – 442 = 552,89 Полученные прогнозные данные отразим в таблице:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
