вопр к зач статистика. Статистика
 Скачать 33.75 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» (ВлГУ) Институт Экономики и менеджмента Вопросы к зачету по дисциплине «Статистика» Выполнил: Студент группы ВЭКу-121 Тихонов В.Е. Проверил: Преподаватель Субботина Н.О. Владимир 2022 1.Сущность, значения и виды статистической сводки и группировки Статистическая сводка (простая сводка) в узком смысле слова представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения. Статистическая сводка (сложная сводка) в широком смысле слова включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей, представление результатов группировки и сводки в виде статистических таблиц. Правильная, научно организованная сводка, опираясь на предварительный глубокий теоретический анализ, позволяет получить все статистические итоги, отражающие важнейшие, характерные черты объекта исследования, измерить влияние различных факторов на результат и учесть все это в практической работе при составлении текущих и перспективных планов. Задача сводки – дать характеристику объекту исследования с помощью систем статистических показателей, выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на трех этапах: определение групп и подгрупп; определение системы показателей; определение видов таблиц. Группировкой называется разбиение общей совокупности единиц объекта на однородные группы по одному или нескольким существенным для них признакам. Признак, по которому производится распределение единиц наблюдаемой совокупности на группы, называютгруппировочным признаком или основанием группировки. Группировка проводится с целью: – установления статистических связей и закономерностей; – построения и описания объекта; – выявление структуры изучаемой совокупности. Каждой из этих целей соответствует особый вид группировки. Виды группировок Типологическая – разбиение разнородной совокупности на качественно однородные группы (типы). Осуществляются посредством сложных неравноинтервальных группировок. Примеры – группировки хозяйственных объектов по формам собственности, работников занятых физ.трудом и преимущ. умственным. Структурная – разделение на однородные группы, характеризующие структуру совокупности по какому-либо признаку. Аналитическая– позволяет выявить взаимосвязь между факторным и результативным признаком. Факторными называются признаки, под воздействием которых изменяются результативные признаки. Простые – разбиение совокупности пот одному признаку. Комбинационные – распределение единиц совокупности одновременно по нескольким признакам. Рекомендуется сначала группировать единицы по качественным признакам, а затем – по количественным. Группируемые данные могут быть неупорядоченными, в этом случае полученная группировка является первичной. Если группировка производится на основании данных первичной группировки, то она относится ко вторичной. 2. Ранговые показатели тесноты связи В анализе социально-экономических явлений часто приходится прибегать к различным условиям оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если отдельные значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называются связными. Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена (ρ) и Кендалла (τ). Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, если их значения будут упорядочены или проранжированны по степени убывания или возрастания признака. Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов): 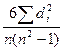 = 1 -  ,где  - квадраты разности рангов;n – число наблюдений (число пар рангов). Коэффициент Спирмена принимает любые значения в интервале 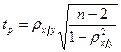 . Значимость коэффициента корреляции рангов Спирмена проверяется на основе t-критерия Стьюдента. Расчетное значение критерия определяется по формуле: .Значение коэффициента корреляции считается статистически существенным, если  .Ранговый коэффициент корреляции Кендалла (τ) может также использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующие однородные объекты и ранжированные по одному принципу. Расчет Ранговый коэффициент корреляции Кендалла (τ) осуществляется по формуле:  ,где n - число наблюдений; S – сумма разностей между числом последовательностей и числом инверсий по второму признаку. Расчет данного коэффициента выполняется в следующей последовательности: значения х ранжируются в порядке возрастания или убывания; значения y ранжируются в порядке, соответствующем значениям x; для каждого ранга y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину P как меру соответствия последовательностей рангов по х и y. Она учитывается со знаком «плюс»; для каждого ранга y определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «минус»; определяется сумма баллов по всем членам ряда. Если в изучаемой совокупности есть связные ранги, то распределение необходимо проводить по следующей формуле: 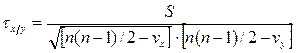 ,где  .Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:  ,где m – количество факторов; n- число наблюдений; S – отклонение суммы квадратов рангов от средней квадратов рангов. В случае наличия связных рангов коэффициент конкордации определяется по формуле 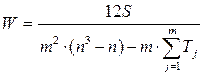 ,где  ;t – количество связных рангов по отдельным показателям. Проверка значимости осуществляется по формуле: 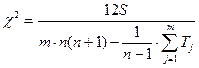 .Коэффициент конкордации принимает любые значения в интервале .Ранговые коэффициенты корреляции Спирмена, Кендалла и конкордации имеют преимущество, что с помощью их можно измерять и оценивать связи как между количествеными, так и между атрибутивными признаками, которые поддаются ранжированию. |