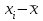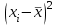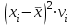Статистикалық жиынтық. 2-дәріс биостатистика. Статистикалы жиынты
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Статистикалық жиынтық – уақытпен және кеңістікпен шектелген қандайда бір нысан белгісінің бірдей жиынтығы (елдегі белгілі бір жылда туылған балалар саны; бір қаладағы тұрғындар саны; берілген елдегі қатерлі ісікпен ауырғандар саны және т.б.). Медициналық-биологиялық, клиникалық, фармацевтикалық және басқа да зерттеулерде, зерттеуші тәжірибесінде ешқашан толық топ нысанын алып, оған жаппай зерттеу жүргізу мүмкін емес, сондықтан таңдамалы әдісті қолданады. Таңдамалы әдіс – статистикалық жиынтықтағы белгілі бір шекті нысанды таңдап және оны зерттеудің статистикалық тексеру әдісі. Таңдамалы әдіс медицинада, денсаулық сақтауда және фармацияда кеңінен қолданыс табуда. Мысалы: белгілі бір патологиялық өзгерісі бар барлық ауруларды зерттеу мүмкін емес, сондықтан олардың кейбіреулерін ғана зерттейді; барлық дәрілік препараттардың стандартқа сай болуын тексеру мүмкін емес, сондықтан оларға таңдамалы бақылау жүргізеді және т.б. Бас статистикалық жиынтық– бұл шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы. Мысалы: белгілі бір патологиялық өзгерісі бар барлық аурулар, сол аймақтың барлық тұрғындары және т.б. Таңдамалы жиынтық (таңдау)– бұл бақылаудың таңдап алынған белгілі бір бөлігінен тұратын, бұл бөлек бас жиынтықты сипаттай алатын элементтердің жиынтығы. Жиынтық көлемі – бұл бақылау элементтерінің жалпы саны. Бас жиынтықтың көлемі «N», ал таңдамалық жиынтықтыңкөлемі – «n» мен белгіленеді. Егер n≤30 болса, онда таңдаманы кіші деп есептеледі. Бақылаудың элементі - бұл зерттелетін құбылыстың жеке дербес жағдайы. Таңдамалы зерттеу әдісі бас жиынтық шексіз немесе зерттеу нысандарды жою жағдайына байланысты болғанда (мысалы, дәрілік препараттарды тексеру) жалғыз мүмкіндігі бар әдіс болып табылады. Сонымен қатар, ол қор шығындарын едеуір үнемдеуге мүмкіндік береді. Бұл әдістің кемшілігі тек нысанның бір бөлігі зерттелетіндіктен қателіктің пайда болуында. Таңдаманың негізгі қасиеті – үлгілігі (репрезентати́втілігі), яғни таңдама сипатамасының бас жиынтықтың сипаттамасына толықтай сәйкес келуі. Ол таңдау арқылы зерттеу нәтижелері қаншалықты таңдау жүргізілген бас жиынтықты сипаттауға қолдануға болатындығын анықтайды. Үлгілі таңдаманың түрі: сапалық – бұл бас және таңдамалыжиынтықтағы бақылау элементтері белгілерінің сәйкес келуі. сандық – бұл жеткілікті бақылау саны. Жүйелік материалдардың статистикалық бақылауының бірінші қадамыстатистикалық үлестірімнің таңдамасын анықтау болып табылады. Статистикалық үлестірімнің таңдамасы (немесе вариациялық қатар) екі бағаннан тұратын кестеден тұрады (1 кесте). Бірінші бағанда нұсқа деп аталатын вариациялық белгінің мәні жазылады және ол «xi» белгіленеді, ал екінші бағанда жиілік деп аталатын және «νi» белгіленген, нұсқаның қанша рет кездескенін көрсететін сандар жазылады. Варацияланатын белгілер дискретті және үздіксіз сипатта болуы мүмкін. Бүтін сандар болатын белгі нұсқаларын дискретті деп атайды. Мысалы, отбасындағы балалар саны, науқастар саны, қораптағы ампула саны және т.б. Егер вариациялық қатардағы нұсқалар дискретті шама түрінде берілсе, онда бұндай вариациялық қатарды дискретті деп атайды. 1 мысал. Жеке зерттелген тетрациклин гидрохлориді белсендігінің алынған мәндеріxi (в ED/мг): 925, 940, 760, 905, 995, 965, 940, 925, 940, 940, 905. Мәндердің белсенділігін және жиілікті өсу ретімен орналастыра отырып, дискретті вариациялық қатар аламыз (2 кесте): 2 кесте
Дискретті вариациялық қатарды полигондеп аталатын көпбұрышты сызбалық түрінде көрсетуге болады (1 сурет). Белгілі-бір аралықтағы кез-келген мәнді қабылдай алатын белгілер нұсқасы үздіксіз деп аталады. Мысалы, артериалді қан қысым, бойы, салмағы, жалақысы және т.б. Үздіксіз белгілер үшін аралық вариациялық қатар құрылады. Берілген аралықағы белгінің ең аз мәні - төменгі аралық шегі, ал ең көп мәні - жоғарғы аралық шегі деп аталады. 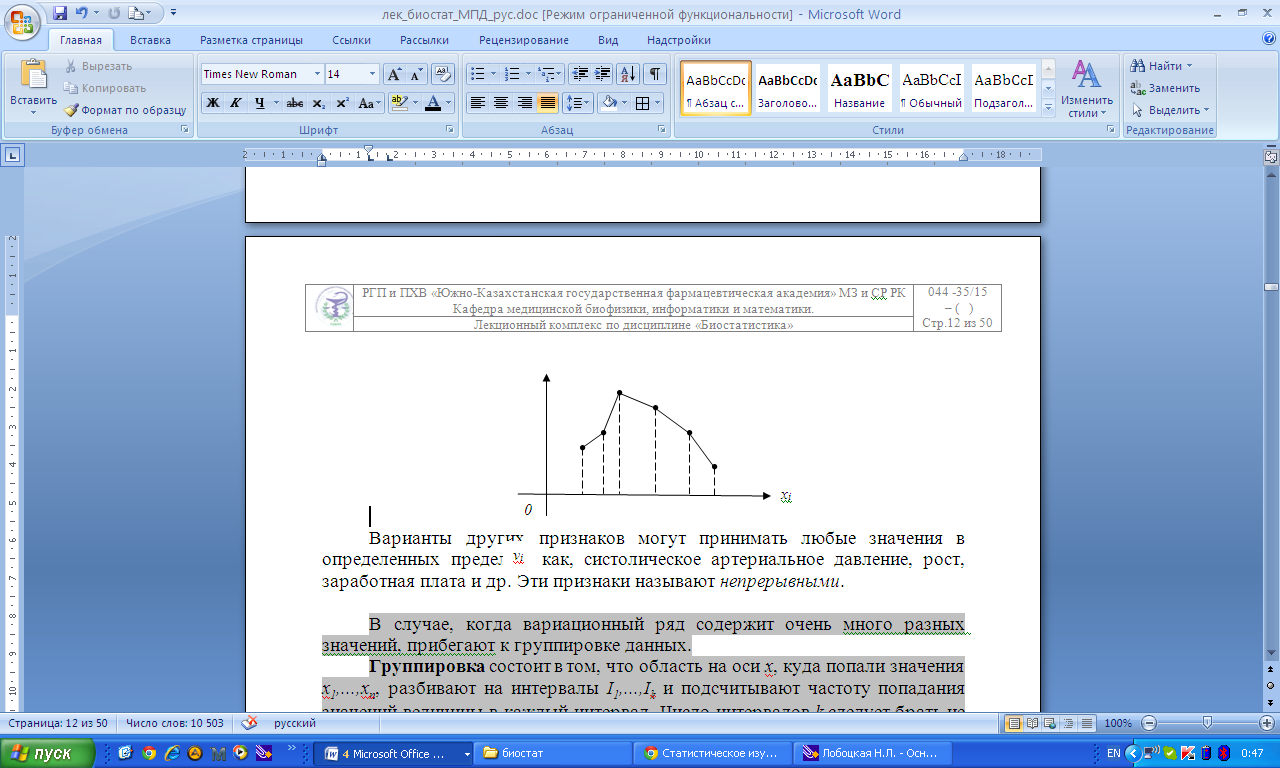 νi 1 сурет. Полигон 2 мысал. Ер адамның (xi) бойының өсуінің аралық вариациялық қатары.
Аралық вариациялық қатарды гистограмма деп аталатын сатылы тұрпат түрдегі сызбамен көрсетуге болады. (2 сурет). 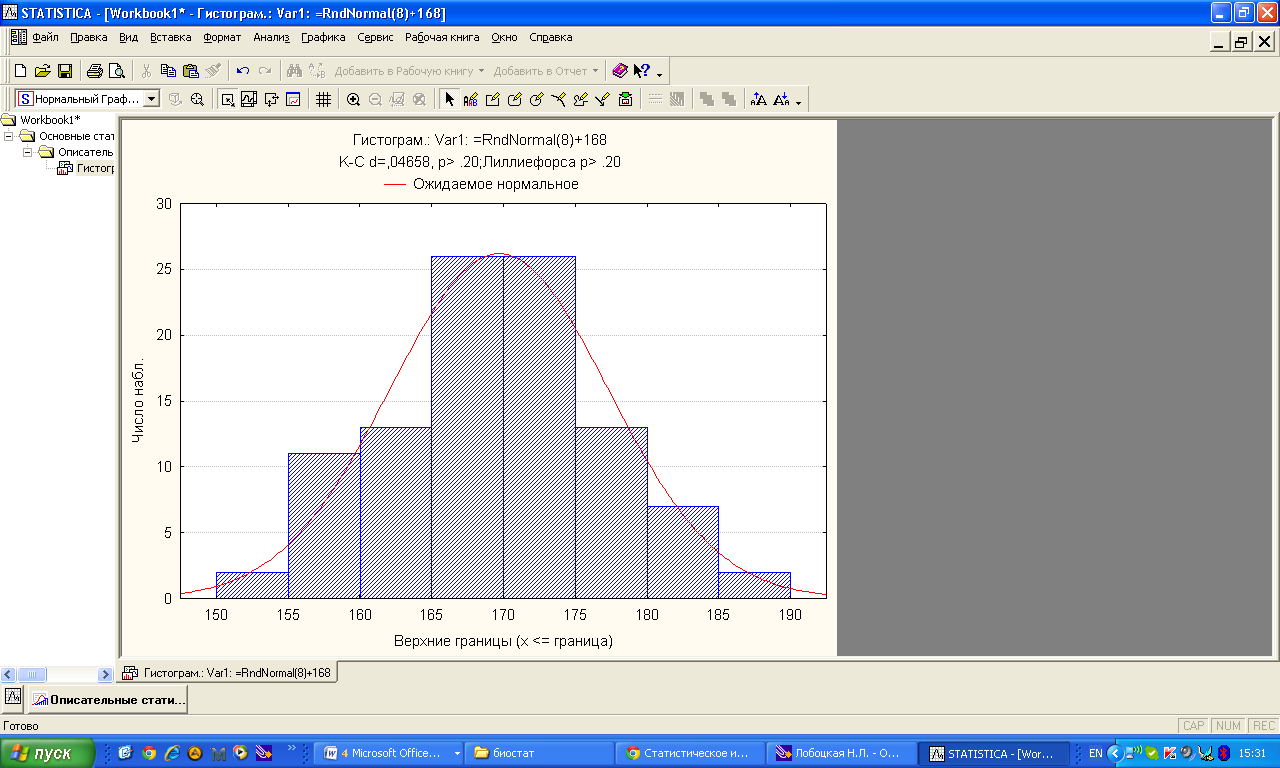 2 сурет. Гистограмма. Аралық вариациялық қатар бақылау саны үлкен болған кезде дискретті белгілер үшін де құрылады. Вариациялық қатар орталық үрдіс (тенденция) көрсеткіштерімен және әр түрлілік (разнообразия) көрсеткіштерімен сипатталады. Орталық үрдіскөрсеткіштеріне орташа және құрылымды шамалар жатады. Орташа шамалар: - Қарапайым орташа арифметикалық шама 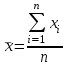 , , ұндағы n - қатардың жалпы саны; - Өлшенген орташа арифметикалық шама 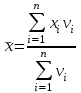 , , мұндағы νi – жиіліктер; - Қарапайым орташа геометриялық шама 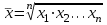 - Қарапайым орташа квадраттық шама 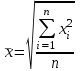 - Өлшенген орташа квадраттық шама 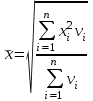 3 мысал. Келесі берілгендер бойынша 18 жастағы ер балалардың орташа салмағын анықтау керек:
Шешуі: 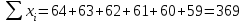 , , 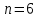 , , 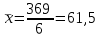 - қарапайымарифметикалықорташа. - қарапайымарифметикалықорташа.4 мысал. Келесі берілгендер бойынша 18 жастағы ер балалардың орташа салмағын анықтау керек:
Шешуі: 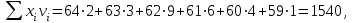 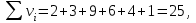 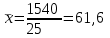 - өлшенген арифметикалық орташа. - өлшенген арифметикалық орташа.Құрылымды шамалар: мода (Мо) – ең үлкен жиіліктегі нұсқа; медиана(Ме) – қатар ортасында орналасқан нұсқа; квантилдер – вариациялық қатарды теңдей жеке бөліктерге бөлетін шама. Төменгі квартиль (Q1) немесе 25-ші процентиль (P25) – бұл таңдаманың 25%-пайызынан төмен жататын кездейсоқ шаманың мәні. Төменгі квартилдің нөмірін анықтайтын формула: 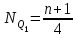 . . Жоғарғы квартиль (Q1) немесе 75-ші процентиль (P75) – бұл таңдаманың 25%-пайызынан жоғары жататын кездейсоқ шаманың мәні. Жоғарғы квартилдің нөмірін анықтайтын формула: 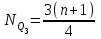 . . Егер квартилдің нөмірі бөлшек болса, онда оны жақын жатқан бүтін санға. 5 мысал. Мода жәнемедиананыкелесіберілгендербойыншаанықтаукерек:
Шешуі: МО=62, МЕ=61,5. 6 мысал. Мода және медиананы келесі берілгендер бойынша анықтау керек:
Шешуі: МО=70, МЕ=70. 7 мысал. Жеке зерттелген тетрациклин гидрохлориді белсендігінің алынған мәндері xi(ED/мг): 925, 940, 760, 905, 995, 965, 940, 925, 940, 940, 905. Квартилдерді анықтау керек. Шешуі: Таңдаманы реттеу керек: 760, 905, 905, 925, 925, 940, 940,940,940, 965, 995 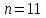 , , 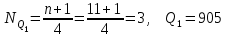 , , 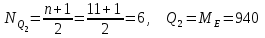 , , 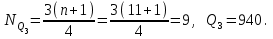 Әр түрлілік көрсеткішіне жататындар: вариациялық қатардыңқұлашы - вариациялық қатардың ең үлкен және ең кіші мәндерінің арасындағы айырым: R=xmax – xmin,мұндағы xmax , xmin – ең үлкен және ең кіші мәндерге байланысты нұсқа; дисперсия – кездейсоқ шаманың оның орташа мәнінен шашырау өлшемі: егертаңдамавариациялыққатартүріндеберілсе, онда дисперсия 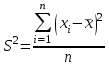 формуласымен анықталады; формуласымен анықталады; егертаңдамакестетүріндеберілсе, онда дисперсия  формуласыменанықталады; формуласыменанықталады; орташа квадраттық ауытқу – кездейсоқ шаманың нұсқадағы өлшем берлігімен берілген, оның орташа мәнінен шашырау шарасы: 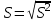 ; ; вариация коэффициенті - кездейсоқ шаманың пайызбен берілген шашырау шарасы: 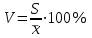 . . Егер V≤ 33% болса, онда таңдама біртекті деп есептеледі. 8 мысал. Вариациялық қатар үшін әр түрлілік көрсеткіштерін анықтау керек.
Шешуі. Таңдамалыорташа: 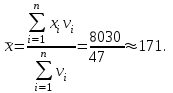 Таңдамалы дисперсия: 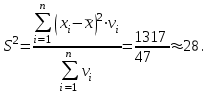 Таңдамалыорташаквадраттықауытқу: 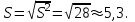 Вариация коэффициенті: 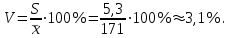 Вариациялыққатардыңқұлашы: 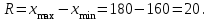
Статистикалық сипаттамаларды «мұртты жәшік» сызбасы арқылы көрсету ыңғайлы. 8-ші мысалдың шарттары үшін орындалған сызбалар (сурет 4 a, b). Бұндай сызбаларды талдаған кезде міндетті түрде «легендағы» яғни сызбаның төменгі жағында берілген шартты белгілерге көңіл аудару керек. 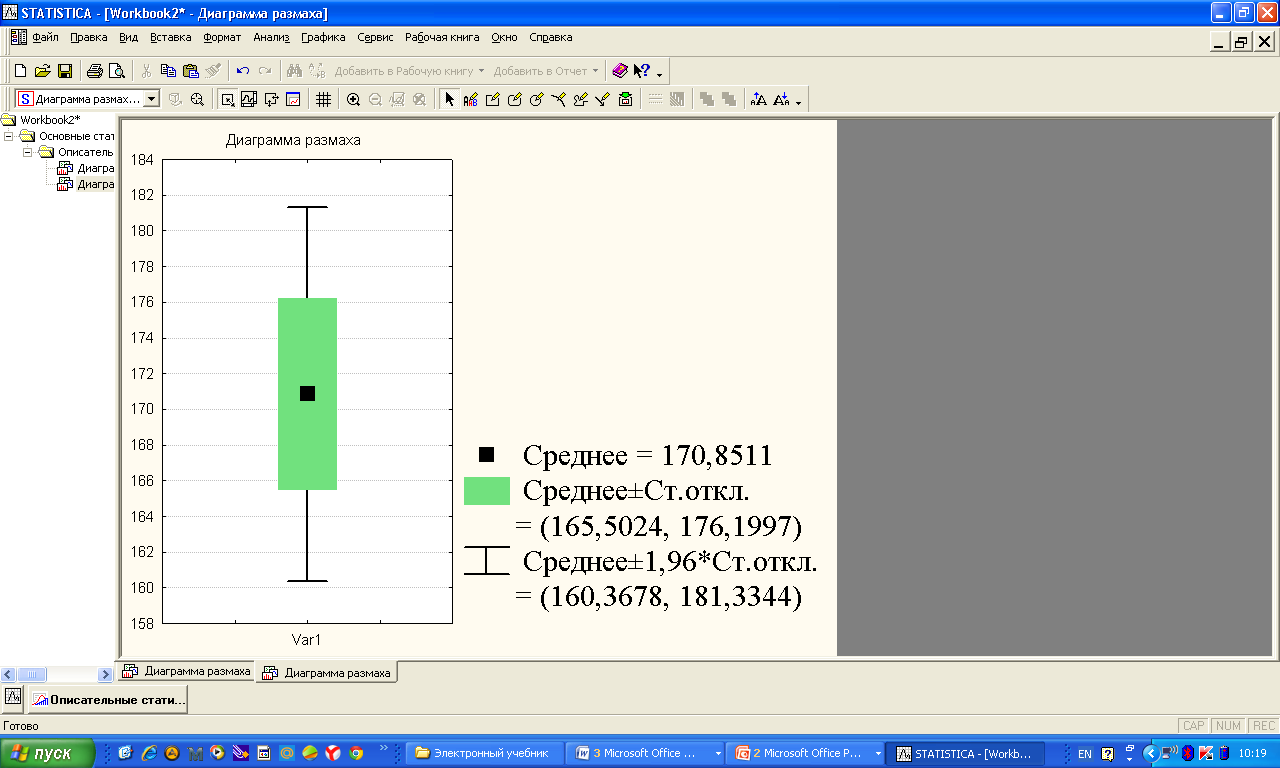 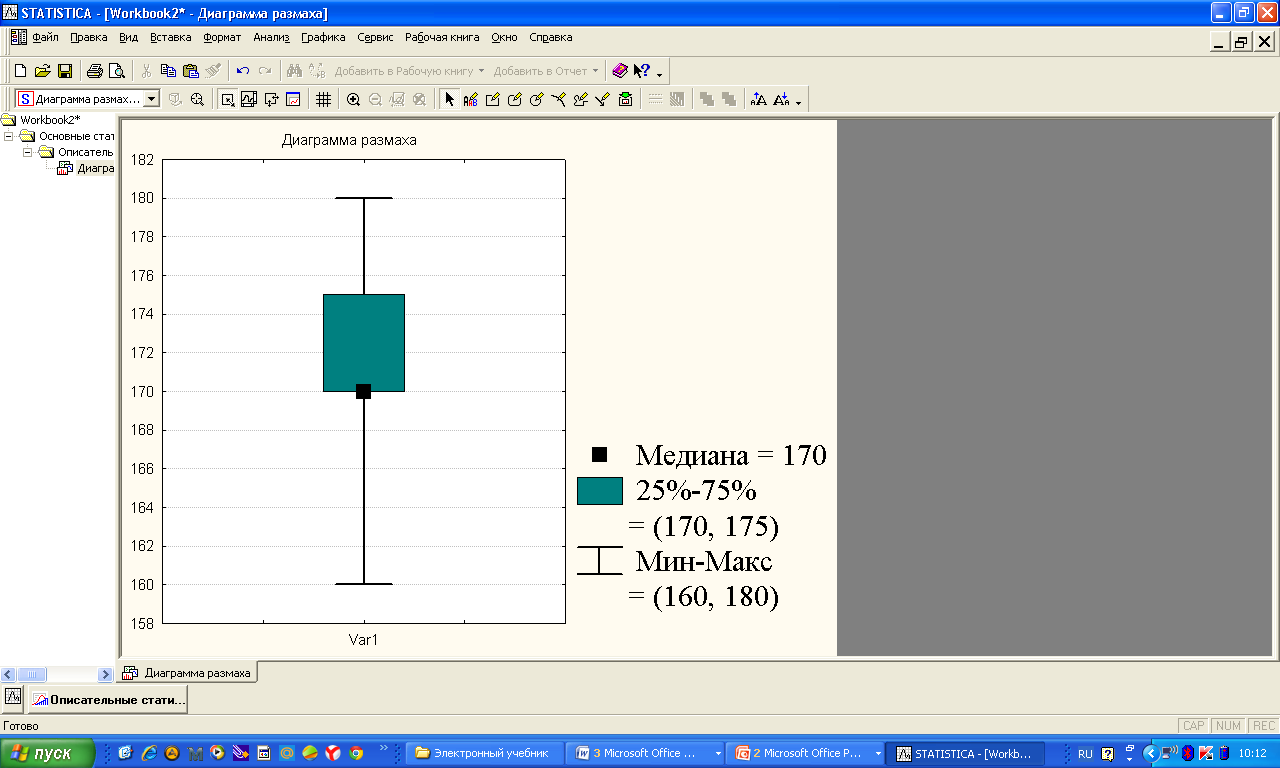 a b 4. сурет. Бірінші сызбада (сурет 4 а) орташа, ең аз және ең көп мәндер, сонымен қатар стандартты ауытқу келтірілген. Екінші сызбада (сурет 4 b) медиана мәні, 25-ші және 75-ші процентиллер келтірілген. Бас жинақтың сипаттамаларын («Х» -бас орташа, «D» - бас дисперсия, «σ» - орташа квадраттық ауытқу) параметрлер деп атайды. Әдетте параметрлер белгісіз және оларды берілген таңдамалар негізінде жуықтап бағалауға болады. Бұл жуық мәндер бас жинақ параметрлерінің бағасы деп аталады. «Х» бас орташаның бағасы, « 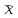 » таңдаманың орташасы болып табылады. » таңдаманың орташасы болып табылады. Зерттелетін белгінің өзінін « 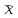 » орташа мәнінін айналасында шашырауын сипаттау үшін «S2» -таңдамалыдисперсия деп аталатын сипаттама енгізіледі. » орташа мәнінін айналасында шашырауын сипаттау үшін «S2» -таңдамалыдисперсия деп аталатын сипаттама енгізіледі.«D» - бас дисперцияның бағасы болып «s2» - түзетілген таңдамалы дисперсия табылады. Түзетілген таңдамалы дисперсия 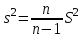 формуласымен анықталады. формуласымен анықталады.«σ» - бас жинақтың орташа квадраттық ауытқуының бағасы болып, «s» - орташа квадраттық ауытқудың түзетілген таңдамасы табылады. Орташа квадраттық ауытқудың түзетілген таңдамасы 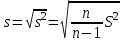 формуласымен анықталады. формуласымен анықталады. « 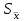 »- орташа қателік немесе орташа квадраттық қателік немесе стандартты орташа қателік деп аталын шама »- орташа қателік немесе орташа квадраттық қателік немесе стандартты орташа қателік деп аталын шама 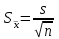 формуласымен анықталады. Бұл шама «n» таңдама көлемімен есептелінген бас жинақтың таңдама орташасының стандартты ауытқуын сипаттайды. формуласымен анықталады. Бұл шама «n» таңдама көлемімен есептелінген бас жинақтың таңдама орташасының стандартты ауытқуын сипаттайды.8 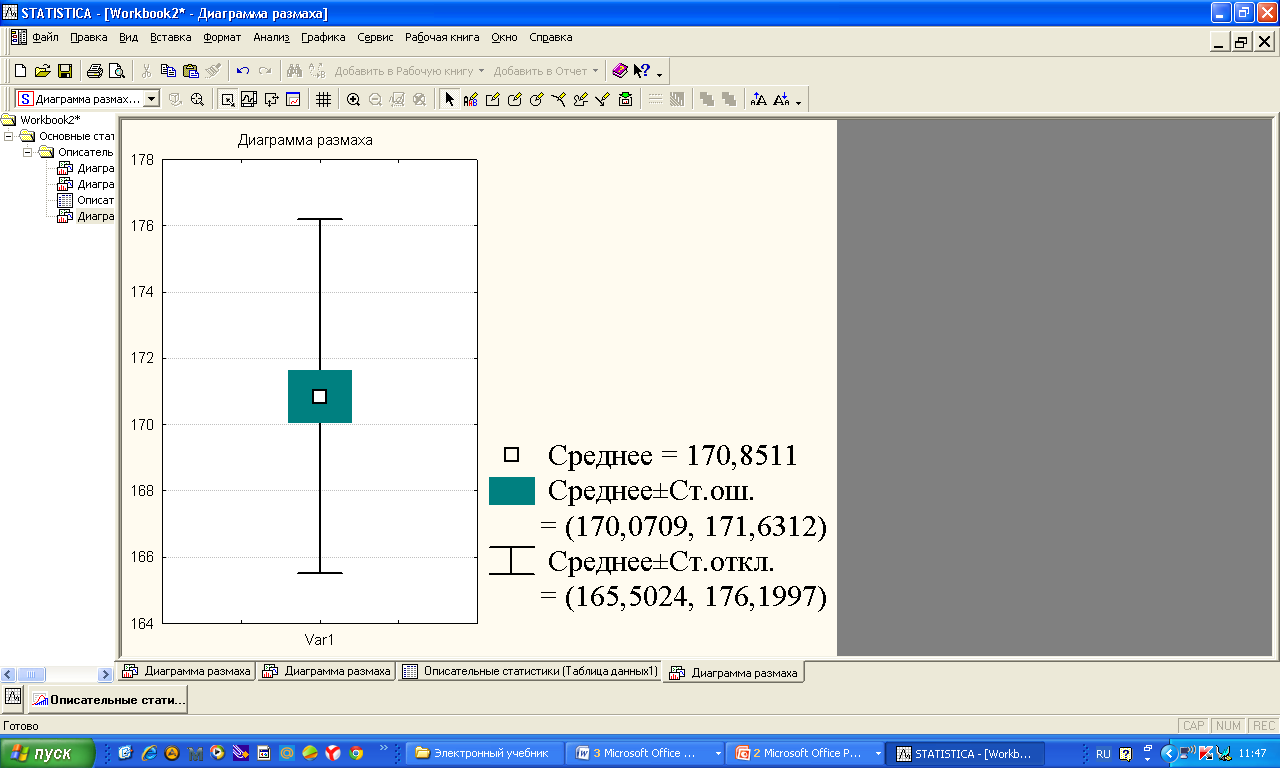 -ші мысалдың шарттары үшін орындалған сызба: Жеке параметрлердің кейбір бағалауы нүктелік бағалауды береді. Бас жинақтың параметрлерінің аралық бағалауы деп «γ» ықтималдылығымен берілгенпараметрді екі жағынан жабатын нақты мәнінің аралығын айтады. Аралық бағалауды сенімділік аралығы, ал соған байланысты «γ»» ықтималдықты сенімділік ықтималдылығы немесе сенімділік (медицина және биологияда γ=0,95) деп атайды. Б 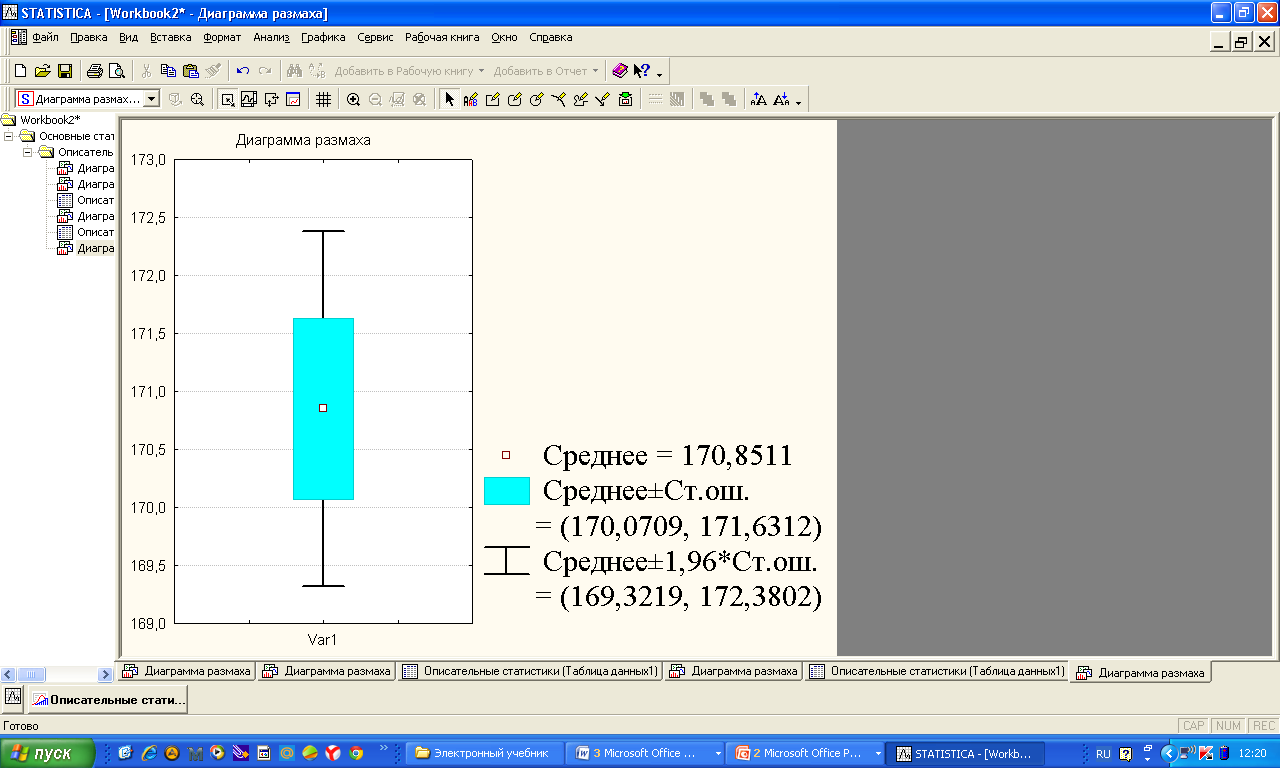 ас орташа үшін сенімділік аралығы 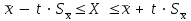 арақатынасынаналынуы мүмкін. Мұндағы «n» бақылаудағы арақатынасынаналынуы мүмкін. Мұндағы «n» бақылаудағы  - таңдамалы орташа, - таңдамалы орташа,  (γ;n-1) – «γ» және «n»-ге тәуелді кестелік шама, (γ;n-1) – «γ» және «n»-ге тәуелді кестелік шама,  - орташаның стандартты қателігі. - орташаның стандартты қателігі.8-ші мысалдың шарттары үшін орындалған сызба. Кез келген медициналық-биологиялық зертеулердің ең бір маңызды кезеңдерінің бірі - бұл қарастырылып отырған таңдама көлемін анықтау. Таңдама көлемін анықтау– медициналық-биологиялық зертеулердің маңызды кезеңі. Егер таңдама көлемі жеткіліксіз болса, онда таңдама сипаттамаларының қателіктерінің артуына және дұрыс емес қорытынды жасауға алып келеді. Таңдама көлемі зерттелетін шаманың орташа квадраттық ауытқуына (σ), қолданылатын белгінің қуатына және маңыздылық деңдейіне (р). тәуелді болады. Таңдама көлемін есептейтін формула: 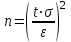 , мұндағы n – таңдама көлемі, σ – орташа квадраттық ауытқу, , мұндағы n – таңдама көлемі, σ – орташа квадраттық ауытқу, 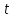 =1,96 – р=0,05 үшін стандартты бірқалыпты үлестірімнің кестелік мәні, ε =0,01 – МЕМСТ-қа сәйкес алынған баға дәлдігі. =1,96 – р=0,05 үшін стандартты бірқалыпты үлестірімнің кестелік мәні, ε =0,01 – МЕМСТ-қа сәйкес алынған баға дәлдігі. |