Стжсін шешу дістері (Гаусс)
 Скачать 26.58 Kb. Скачать 26.58 Kb.
|
|
СТЖ-сін шешу әдістері (Гаусс). СТЖ-сін элементар түрлендірулер матрицаның жолдарына қолданылатын элементар түрлендірулерге ұқсас. Сондықтан ондай түрлендірулерді әдетте жүйенің өзіне емес, оның кеңейтілген матрицасына қолданылады. Теорема. Элементар түрлендірулер қолданғаннан жүйенің шешулері өзгермейді, яғни оған тең күшті жүйе алынады. Осы теоремаға сүйеніп берілген жүйені оңай шешілетін жүйеге келтіру әдісі – СТЖ-сін шешудің Гаусс әдісі немесе айнымалыларды біртіндеп жою әдісі деп аталады. Бұл әдіс бойынша берілген СТЖ-ң кеңейтілген матрицасын сатылы түрге келтіреді. Нәтижесінде мына жағдайлардың біріне келеміз: 1 жағдай. рангАн≠рангАк. Бұл – соңғы жүйеде қайшы теңдеу шығады деген сөз. Онда соңғы жүйе және оған тең күшті болатын берілген жүйе үйлесімсіз (өткен тақырыптағы таблицаны қара). 2 жағдай. рангАн=рангАк=n. Бұл жағдайда соңғы жүйенің түрі үшбұрыш түрінде болып шығады. Бұл – берілген жүйе үйлесімді анықталған деген сөз. Үшбұрышты жүйенің соңғы теңдеуінен хn айнымалысының бір ғана мәні табылады. 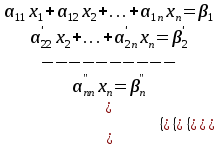 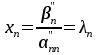 . Осы мәнді соңынан екінші тұрған теңдеудегі xn-ң орнына қойып xn-1 айнымалысының бір ғана мәнін табады. Осылайша жоғары көтеріле отырып үшбұрышты жүйеден барлық айнымалының мәндерін табады. Сонда берілген жүйенің . Осы мәнді соңынан екінші тұрған теңдеудегі xn-ң орнына қойып xn-1 айнымалысының бір ғана мәнін табады. Осылайша жоғары көтеріле отырып үшбұрышты жүйеден барлық айнымалының мәндерін табады. Сонда берілген жүйенің 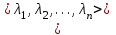 түрінде бір ғана шешуі алынады. түрінде бір ғана шешуі алынады.СТЖ шешіңіз: 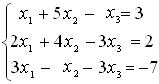 Шешуі 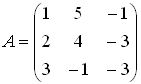 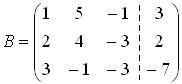 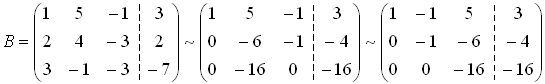 |
