Тсау. Ганбат М. ТСАУ. Структурная схема сар представлена на рис. 1
 Скачать 363.57 Kb. Скачать 363.57 Kb.
|
|
Исходные данные 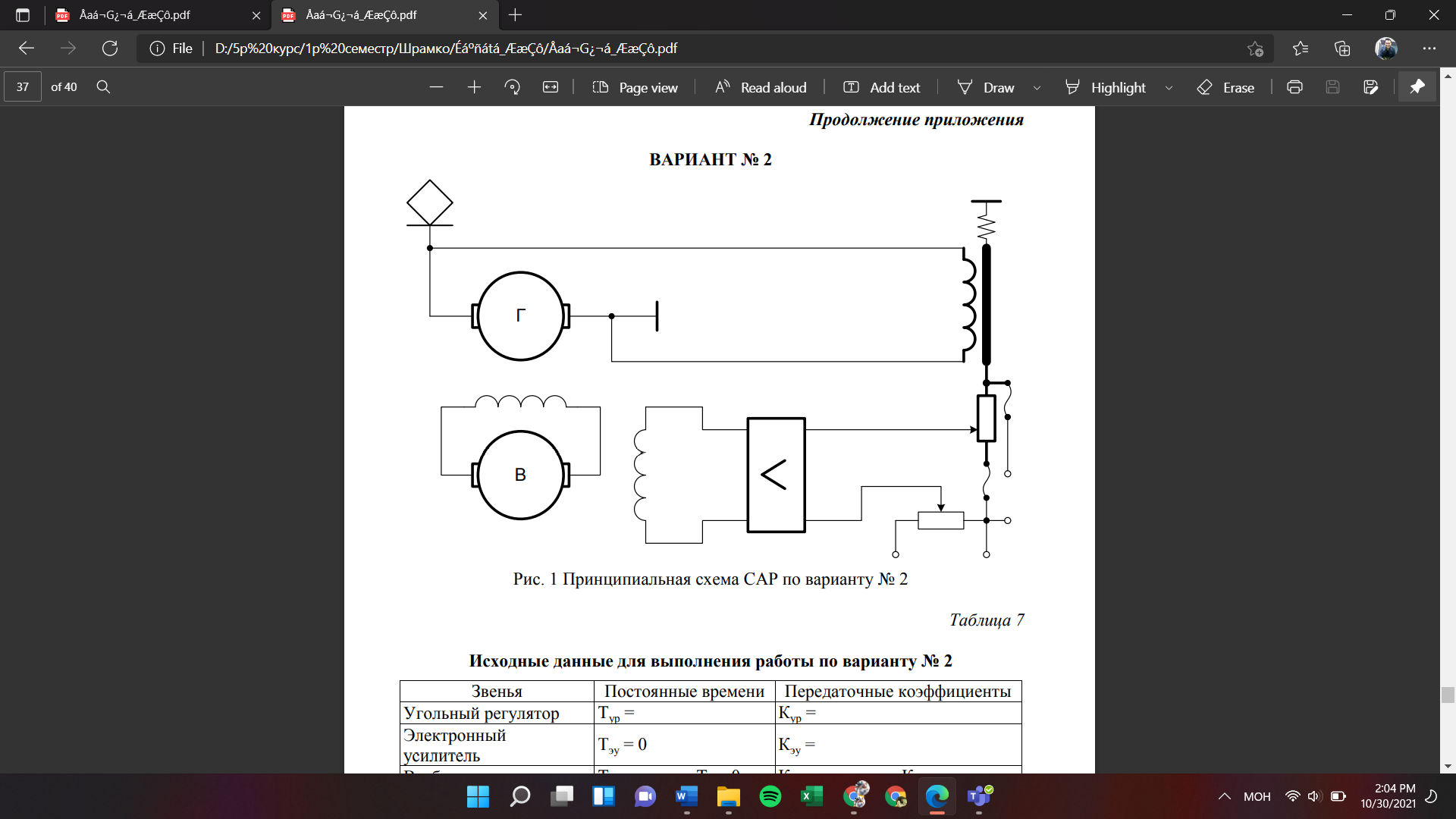  1 Вариант № 64    2 7 6  УР   R2 3   8 ЭУ     4 ОВВ 5 9  R1 Таблица 1
Структурная схема САР  ЭС Структурная схема САР представлена на рис. 1.1.                Iовв Uэу Uн Iовг Uв ∆U UЗ В ОР ОВГ ЭУ ОВВ             UГ UУР УР САР разделена на следующие звенья: 1) элемент сравнения (ЭС) – производит сравнение заданного напряжения с напряжением тахогенератора, реализован в виде схемного решения осуществляющего вычитание двух напряжений по формуле (1.1); 2) электронный усилитель (ЭУ) – усиливает сигнал рассогласования до необходимой величины (входная величина U, выходная – Uэу); 3) обмотка возбуждения возбудителя (ОВВ) – обеспечивает необходимое возбуждение возбудителя (входная величина Uэу, выходная – Iовв); 4) возбудитель (В) – обеспечивает питания обмотки возбуждения генератора (входная величина Iовв, выходная – Uв); 5) обмотка возбуждения возбудителя (ОВВ) – обеспечивает необходимое возбуждение возбудителя (входная величина Uв, выходная – Iовг); 6) обмотка возбуждения генератора (ОВГ) – обеспечивает необходимое возбуждение генератора (входная величина Uв, выходная – Iовг); 7) объект регулирования (ОР) (генератор) – создёт ЭДС генератора (входная величина Iовг, выходная - Uг); 8) обратная связь (ОС) (угольной регулятор) – измеряет фактическое значение регулируемой величины (входная величина Uг, выходная – Uур). 1.1 Описание принципиальной схемы Принципиальная схема САУ приведена на рис 1. На схеме сделаны следующие обозначения: 1- нагрузка(H); 2 - якорь генератор(Г); 3 - обмотки возбуждение генератора(ОВГ); 4 – якорь возбудитель(В); 5 – обмотки возбуждение возбудитель(ОВВ); 6 – электронный усилитель(ЭУ); 7 – угольный регулятор(УР); 8 – потенциометр обратной связи(R2); 9 – потенциометр(R2); Так как в системе применена отрицательная обратная связь то при отсутствии возмущающих воздействий (U = const), величина напряжения на входе электронного усилителя будет определяться разностью заданного напряжения UЗ и напряжения на угольный регуляторе Uур: U = UЗ – Uур. При отсутствии возмущающих воздействий и неизменном задающем напряжении UЗ скорость вращения двигателя и тахогенератора постоянна, поэтому U = const. Следовательно, система будет находиться в равновесии, и все переменные описывающие ее поведение будут оставаться неизменными. При возникновении возмущающего воздействия изменится скорость вращения генератора, что приведет к изменению величины Uур на величину Uур. Это в свою очередь вызовет изменение разницы: U = UЗ – (Uур Uур). Величина Uур будет иметь знак, соответствующий направлению изменения числа оборотов двигателя либо в сторону увеличения, либо в сторону уменьшения. Под действием изменившейся величины U изменится напряжение на выходе электронного усилителя, что вызовет изменение тока в обмотке возбуждения возбудителя, а это, соответственно, вызовет изменение напряжения на якоре генератора, что повлечет за собой изменение скорости вращения генератора. Возбуждение двигателя осуществляется обмоткой возбуждения (ОВГ), питающейся от возбудителя. Переходной процесс в САР будет протекать до тех пор, пока система не придет в равновесное состояние и скорость вращения генератора не установится в соответствии с новыми условиями. Угольные регуляторы напряжения Действие угольных регуляторов основано на том, что сопротивление сталбика, составленянного из угольных дисков, уменьшается с увеличением приложенного к ним усилия. УР представляет собой угольных дисков, сжатых пружиной. Эта пружина, в свою очередь, соединена с сердечником соленоида, к обмотке которого подведено полное напряжение регулятора. При увеличении напряжения на зажимах генератора, сила, сжимающая угольный столбик, уменьшается вследствие того, что соленоид усилия пружины. Угольный столбик включен последствательно с обмоткой генератора и таким образом регулируем напряжения генератора. 2. Передаточные функции динамических звеньев Для создания общей методики расчета различных САР удобно ввести понятие типового динамического звена. Под типовым динамическим звеном понимают устройство любого физического вида и конструктивного исполнения, описываемое определенным типов дифференциального уравнения. Для упрощения процесса расчета САР все нелинейные дифференциальные уравнения приводят к линейным, переводят в операторную форму и записывают в стандартной форме. Основные правила записи в операторную форму выглядят следующим образом: (dx / dt) = p x; (d2x / dt2) = p2 x; ∫x dt = x / p; ∫∫x dt = x / p2 где p – оператор Лапласа. Под стандартной формой записи уравнения понимают следующую группировку членов дифференциального уравнения: в левой части выделяется только выходная величина со своими коэффициентами (постоянными времени), а в правой входная величина и возмущающие воздействия со своими коэффициентами (коэффициентами передачи). Для последующих расчетов вводят понятие передаточной функции. Передаточной функцией динамического звена при нулевых начальных условиях и равенстве нулю возмущающих воздействий называется отношение изображений по Лапласу-Карсону выходной и входной величин. Обозначение передаточной функции динамического звена в операторной форме принято как w(p), где p –ператор Лапласа. 2.2. Элемент сравнения В рассматриваемом примере (рис. 1) в качестве элемента сравнения используется схема вычитания двух напряжений. Уравнение, связывающее входное напряжение усилителя с задающим напряжением и напряжением цепи обратной связи, имеет вид: ∆U = UЗ – Uур. Чаше всего при расчетах систем автоматической стабилизации работающих по замкнутому циклу считается, что элемент сравнения идеален, т. е. не вносит погрешность в процесс регулирования. Данное допущение не сказывается на точности, так как погрешность элемента сравнения можно учесть в виде дополнительного возмущающего воздействия в замкнутой системе. 2.3. Электронный усилитель Рассматривать уравнение, описывающее работу электронного усилителя, можно только при наличии его принципиальной схемы. Кроме того, так как электронные усилители имеют очень малую инерционность, то ее величиной обычно пренебрегают, считая усилитель безинерционным звеном. В результате имеем: Uэу = kэу ∆U, где ∆U – напряжение на входе ЭУ; Uэу – напряжение на выходе ЭУ; kэу – коэффициент передачи усилителя. Передаточная функция звена при нулевых начальных условиях может быть найдена как отношение изображений по Лапласу–Карсону выходной и входной величин. Для электронного усилителя с уравнением (4.2) она будет иметь вид: wэу(p) = kэу, wэу(p) = 550. 2.4. Генератор постоянного тока независимого возбуждения Генератор независимого возбуждения можно представить как в виде одного типового динамического звена, так и в виде нескольких звеньев включенных последовательно. Рассмотрим генератор в виде нескольких динамических звеньев. Передаточную функцию для генератора – одного звена можно будет получить перемножением передаточных функций отдельных его составляющих. Обмотка возбуждения. Передаточная функция обмотки возбуждения, как апериодического звена первого порядка, имеет вид: wов(p) = kов / (Tов p + 1), wов(p) = 1 / (0,02 p + 1), Для обмотки возбуждения возбудителем имеет: wовв(p) = kовв / (Tовв p + 1), wов(p) = 1,3 / (0,04 p + 1), Якорь генератора – безинерциальное звено первого порядка. На основании известной характеристики генератора независимого возбуждения (рис. 3) можно определить коэффициент передачи для цепи якоря. Если из анализа работы САР известно, что ток возбуждения и напряжение на якоре в процессе работы мало отклоняются от нулевых начальных условий, то можно воспользоваться методом графической линеаризации. Передаточная функция якоря генератора будет иметь вид: wг(p) = kг / (Tг p + 1), wг(p) = 0,2 / (0 p + 1). Для обмотки возбуждения возбудителем имеет: Wв(p) = kв, Wв(p) = 1,5. 2.5. Угольный регулятор Всвязи с тем, что угольный регулятор является апериодическим звеном первого порядки, передаточная функция имеет вид: Wур(p) = kур / (Tур p + 1), Wур(p) = 0,07 / (0,14 p + 1). 3. Построение частотных характеристик звеньев 3.1 Частотные характеристики Амплитудно-фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости. Она представляет собой геометрическое место точек концов векторов (годограф), соответствующих комплексу частотной передаточной функции при изменении частоты от нуля до бесконечности. По оси абсцисс откладывается вещественная часть, соответствующая комплексу частотной передаточной функции звена, а по оси ординат ее мнимая часть. Задаваясь различными значениями частоты в диапазоне - < ω < +. АФЧХ строят по выражению частотной передаточной функции, она получается из передаточной функции звена в операторной форме записи w(p) подстановкой значение p = jω: W(jω) = A(ω) ejψ(ω) = u(ω) + jv(ω), где A(ω) – модуль частотной передаточной функции; ψ(ω) – аргумент частотной передаточной функции; u(ω) – вещественная часть частотной передаточной функции; v(ω) – мнимая часть частотной передаточной функции. По результатам вычисления модуля и аргумента частотной передаточной функции для всего диапазона частот можно построить отдельно АЧХ и ФЧХ. Амплитудная частотная характеристика (АЧХ) показывает, как звено пропускает сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. По оси абсцисс откладывается значение модуля соответствующее комплексу частотной передаточной функции звена A(ω) – отношение амплитуд выходной и входной величин, а по оси ординат значения частоты в диапазоне - < ω < +. АЧХ строят по выражению A(ω). Фазовая частотная характеристика (ФЧХ) показывает фазовые сдвиги, вносимые звеном в сигнал на различных частотах. По оси абсцисс откладывается значение аргумента соответствующее комплексу частотной передаточной функции звена ψ(ω) – фазовый сдвиг выходной величины по отношению к входной, а по оси ординат значения частоты в диапазоне - < ω < +. ФЧХ строят по выражению ψ(ω). Для апериодического звена второго порядка (двигатель) при построении ФЧХ знаменатель частотной передаточной функции удобнее представить в виде двух сомножителей. 3.2 Угольный регулятор Для обмотки воздуждения: Wур(p) = kур / (Tур p + 1), Wур(p) = 0,07 / (0,14 p + 1). При p = jω Wур(jω) = 0,07 / (0,14 jω + 1). Амплитудная частотная характеристика задаётся выражением: Аур(ω) = 0,07 / ((0,14 ω)2 + 1)0.5. Фазовая частотная характеристика задаётся выражением: ψ(ω) = -arctg(ω‧0,14). Преобразом Wур(jω) используя стандартные формулы комплексных чисел: 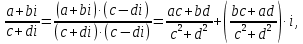 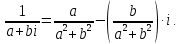 Произведением двух комплексных чисел 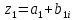 и и 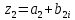 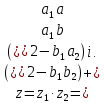 Получим АФЧХ задаётся выражением: 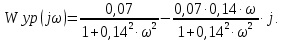 По полученым формулам произведём расчет характеристика. Для положительных значений ω. 4. Передаточная функция САР 4.1. Структурная схема САР         Wовв(p) Wов(p) WВ(p) Uг(p) Wу(p)           Wур(p) 4.1. Структурная схема САР 4.2. Передаточная функция разомкнутой системы Передаточная функция разомкнутой системы будет равны производенны передаточных функцей отдельных звеньев: 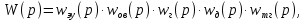 где W(p) – передаточная функция разомкнутой системы. Для рассматриваемого примера имеем следующее выражение: 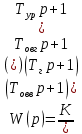 где K – коэффициент усиления САР, 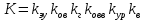 . .В численном виде: 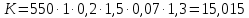 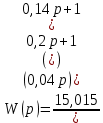 Преобразуем: 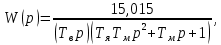 | ||||||||||||||||||
