Задачи студентам 2 курса МСФ. Студентам 2 курса мсф. Задачи для подготовки к экзамену по теоретической механике. Применение теоремы о движении центра масс
 Скачать 475 Kb. Скачать 475 Kb.
|
|
Студентам 2 курса МСФ. Задачи для подготовки к экзамену по теоретической механике. Применение теоремы о движении центра масс. 1. 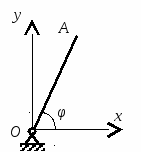 Однородный прямолинейный стержень OA вращается вокруг неподвижной оси, перпендикулярной стержню и проходящей через его конец О, в соответствии с уравнением φ=πt2/2. Установить направление главного вектора внешних сил, действующих на стержень при t=0. 2. М 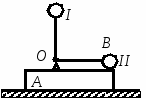 еханическая система состоит из тела А массы m1, которое может перемещаться поступательно по гладкой горизонтальной плоскости, и шарнирно прикрепленного к нему невесомого стержня длины l с точечным грузом B массы m2. В начальный момент времени система находилась в покое, а стержень OB занимал положение I. Найти перемещение тела А при повороте стержня OBв положение II. еханическая система состоит из тела А массы m1, которое может перемещаться поступательно по гладкой горизонтальной плоскости, и шарнирно прикрепленного к нему невесомого стержня длины l с точечным грузом B массы m2. В начальный момент времени система находилась в покое, а стержень OB занимал положение I. Найти перемещение тела А при повороте стержня OBв положение II.3. О 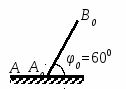 днородный стержень АВ длины 2l опирается концом А на гладкую горизонтальную плоскость. В начальный момент угол наклона стержня к плоскости равен 600. Затем стержню предоставляют возможность из состояния покоя свободно опускаться на плоскость. Найти смещение А0А опорного конца стержня к моменту, когда угол наклона стержня к плоскости станет равным 300. днородный стержень АВ длины 2l опирается концом А на гладкую горизонтальную плоскость. В начальный момент угол наклона стержня к плоскости равен 600. Затем стержню предоставляют возможность из состояния покоя свободно опускаться на плоскость. Найти смещение А0А опорного конца стержня к моменту, когда угол наклона стержня к плоскости станет равным 300.4. 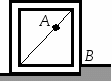 По проволочной направляющей вдоль диагонали вертикальной квадратной рамы массы m, стоявшей неподвижно на гладкой горизонтальной плоскости, отпущен из состояния покоя точечный груз А такой же массы. Найти реакцию упора В, препятствующего смещению рамы на опорной плоскости. 5. На покоящейся непривязанной шлюпке массой m находятся два человека, массы которых равны m1 и m2. Что произойдет со шлюпкой, если первый человек переместится по направлению к корме на расстояние l1, а второй – к носу на расстояние l2? 6 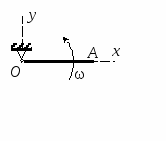 . . Однородный стержень ОА массой m = 10 кг вращается равномерно с угловой скоростью ω = 10 с-1. Определить модуль главного вектора внешних сил, действующих на стержень, если его длина ОА = 1 м. 7. Т 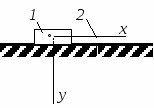 ело 1 массой 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент времени система находилась в покое. ело 1 массой 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент времени система находилась в покое.Применение теоремы об изменении количества движения. 1. Материальная точка массы m равномерно движется по окружности со скоростью v. Найти импульс S равнодействующей сил, приложенных к точке, за время прохождения четверти окружности. 2 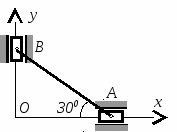 . . В данный момент времени скорость ползуна А линейки АВ эллипсографа равна v= 1м/с, а линейка составляет с осью Ox угол 300. Масса линейки равна 2 кг, длина – 1 м. Пренебрегая массой ползунов и считая линейку тонким однородным стержнем, определить модуль количества движения линейки. 3. 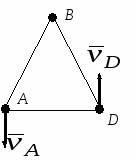 Механическая система из 3-х материальных точек одинаковой массы m, размещенных в вершинах равностороннего треугольника, движется в плоскости рисунка. В изображенном положении скорости точек А и D перпендикулярны линии AD; vA= vD= v. Определить модуль и направление вектора количества движения системы в данном ее положении. 4. 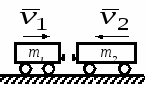 Два вагона масс m1 = 20 т и m2 = 30 т, двигаясь навстречу друг другу по прямолинейному участку пути со скоростями v1 = 3 м/с и v2 = 2,5 м/с соответственно, сцепляются после соударения. Пренебрегая сопротивлениями движению, определить модуль и направление скорости сцепа. 5. Снаряд противотанковой пушки, имеющий массу 6 кг, ударившись о лобовую броню танка, масса которого равна 30 т, под углом к ней 300, рикошетирует. Найти изменение скорости танка, если скорость снаряда равна 500 м/с. 6. 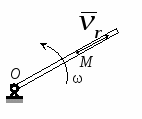 Трубка вращается с угловой скоростью ω = 10 с-1. Относительно трубки движется шарик М массой m =0,2 кг со скоростью 7. 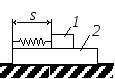 Тело 1 массой 2 кг под действием пружины движется относительно тела 2 массой 8 кг по закону 8 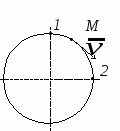 . . Материальная точка М массой m = 1 кг равномерно движется по окружности со скоростью v = 4 м/c. Определить модуль импульса равнодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2. Применение теоремы об изменении кинетического момента. 1. 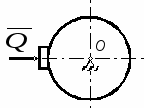 Цилиндрический вал массы m = 10 кг и радиуса r = 10 см вращается с частотой n = 600 об/мин относительно продольной центральной оси. С какой силой Q надо прижать тормозную колодку к валу, чтобы остановить его за t = 10 с, если коэффициент трения скольжения колодки о вал равен f = 0,4, а радиус инерции ρ= 0,3 м. Трением на опорах вала пренебречь. Цилиндрический вал массы m = 10 кг и радиуса r = 10 см вращается с частотой n = 600 об/мин относительно продольной центральной оси. С какой силой Q надо прижать тормозную колодку к валу, чтобы остановить его за t = 10 с, если коэффициент трения скольжения колодки о вал равен f = 0,4, а радиус инерции ρ= 0,3 м. Трением на опорах вала пренебречь. 2. 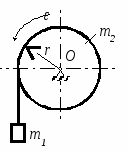 Груз массы m1 подвешен на нити, обмотанной вокруг цилиндрического барабана массы m2 и радиуса r. Пренебрегая трением и массой нити, определить угловое ускорение ε барабана. 3. 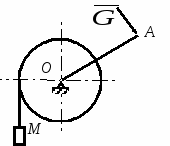 Груз М массой m1 поднимается при помощи ворота. Масса барабана ворота равна m2, радиус барабана R, длина рукоятки OA=l. Считая силу 4. 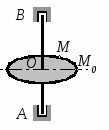 Однородный горизонтальный диск радиуса r и массой m1 может вращаться вокруг неподвижной вертикальной оси AB. По ободу диска движется материальная точка М массой m2 по закону 5. Однородный горизонтальный диск радиусом r и массой m1 вращается вокруг неподвижной вертикальной оси AB, проходящей через его центр О, с угловой скоростью ω0. В некоторый момент от центра диска по его радиусу начинает двигаться материальная точка М массой m2 с постоянной скоростью 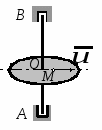 6. 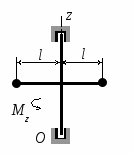 Система состоит из однородного горизонтального стержня длины 2l и массы m, а также двух точечных масс m, закрепленных на его концах. Система начинает вращаться из состояния покоя вокруг неподвижной вертикальной оси Оz под действием постоянного вращающего момента Mz. Определить зависимость угловой скорости от времени t. 7. 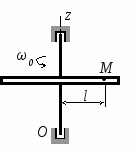 Трубка вращается вокруг вертикальной оси Oz, ее момент инерции Iz = 0,075 кг∙м2. По трубке под действием внутренних сил системы движется шарик М массой m = 0,1 кг. Когда шарик находится на оси Oz, угловая скорость ω0 = 4 с-1. При каком расстоянии l угловая скорость равна 3 с-1? 8. 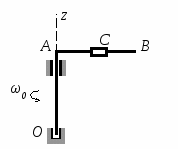 По стержню АВ движется ползун С согласно закону АС = 0,2+1,2 t. Ползун считать материальной точкой массы m = 1 кг. Момент инерции вала ОА со стержнем Iz = 2,5 кг∙м2. Определить угловую скорость вала в момент времени t = 1 с, если начальная угловая скорость ω = 10 с-1. Применение теоремы об изменении кинетической энергии. 1 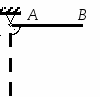 . . Однородный стержень длиной l и массой m, который может вращаться вокруг горизонтальной оси А, отклонен от устойчивого положения равновесия на 900 и отпущен без начальной скорости. Найти угловую скорость стержня в момент, когда он будет занимать вертикальное положение. Сопротивлением воздуха и трением пренебречь. 2. Однородный цилиндр, получив начальную скорость центра, равнуюv0, катится без скольжения вверх по наклонной плоскости. Пренебрегая трением качения и сопротивлением воздуха, определить, на какую высоту поднимется центр цилиндра. 3. 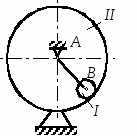 Колесо І массой m1 может катиться без скольжения в вертикальной плоскости внутри неподвижной шестерни ІІ и приводится в движение кривошипом АВ, длиной l и массой m. В начальный момент кривошип составлял угол α = 600 с вертикалью и был отпущен без начальной скорости. Определить его угловую скорость в момент прохождения через равновесное положение. Кривошип считать однородным стержнем, колесо І – однородным диском. Трением пренебречь. Колесо І массой m1 может катиться без скольжения в вертикальной плоскости внутри неподвижной шестерни ІІ и приводится в движение кривошипом АВ, длиной l и массой m. В начальный момент кривошип составлял угол α = 600 с вертикалью и был отпущен без начальной скорости. Определить его угловую скорость в момент прохождения через равновесное положение. Кривошип считать однородным стержнем, колесо І – однородным диском. Трением пренебречь.
с начала движения точки. 5. 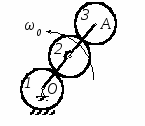 В планетарном механизме кривошип ОА вращается с угловой скоростью ω0. Радиусы колес 6. 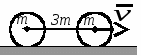 Механическая система состоит из двух одинаковых колес массы m каждое и прямолинейного однородного стержня, соединяющего оси этих колес. Пренебрегая проскальзыванием колес по горизонтальной опорной плоскости и считая их однородными сплошными дисками, найти кинетическую энергию всей системы, если масса соединительного стержня равна 3m, а скорость центра одного из колес равна v. Механическая система состоит из двух одинаковых колес массы m каждое и прямолинейного однородного стержня, соединяющего оси этих колес. Пренебрегая проскальзыванием колес по горизонтальной опорной плоскости и считая их однородными сплошными дисками, найти кинетическую энергию всей системы, если масса соединительного стержня равна 3m, а скорость центра одного из колес равна v.7. 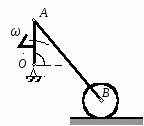 Определить кинетическую энергию механизма, состоящего из кривошипа ОА массы 3m и длины l, шатуна АВ массы m и шарнирно связанного с ним колеса массы m, катящегося без скольжения по горизонтальной плоскости. Кривошип ОА вращается с угловой скоростью ω и в рассматриваемый момент времени вертикален. Кривошип и шатун считать однородными тонкими стержнями; масса колеса равномерно распределена по его ободу. Определить кинетическую энергию механизма, состоящего из кривошипа ОА массы 3m и длины l, шатуна АВ массы m и шарнирно связанного с ним колеса массы m, катящегося без скольжения по горизонтальной плоскости. Кривошип ОА вращается с угловой скоростью ω и в рассматриваемый момент времени вертикален. Кривошип и шатун считать однородными тонкими стержнями; масса колеса равномерно распределена по его ободу.8. 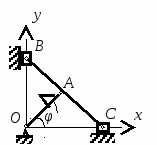 Найти кинетическую энергию эллипсографа, если ОА=АВ=АС= =l, угловая скорость кривошипа ОА равна ω, масса звеньев составляет 9. 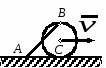 Однородное тонкое кольцо массы m и радиуса R катится без скольжения по горизонтальной плоскости, при этом центр С кольца имеет постоянную скорость 10. 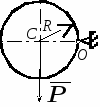 Однородный круглый диск веса P и радиуса R может вращаться вокруг горизонтальной оси О в вертикальной плоскости. В начальный момент радиус ОС горизонтален и диск отпущен без начальной скорости. Пренебрегая трением, определить угловую скорость ω диска в момент, когда диск повернется на угол 300. 11. 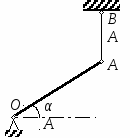 Однородный прямолинейный стержень ОА длины l, закрепленный в вертикальной плоскости с помощью шарнира О и нити АВ, составляет угол α= 300 с горизонтом. Пренебрегая сопротивлениями, найти наибольшую угловую скорость стержня при обрыве нити АВ. 12. 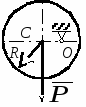 Однородное тонкое кольцо веса P и радиуса R может вращаться вокруг горизонтальной оси О в вертикальной плоскости. В начальный момент времени линия ОС ( Однородное тонкое кольцо веса P и радиуса R может вращаться вокруг горизонтальной оси О в вертикальной плоскости. В начальный момент времени линия ОС (13. 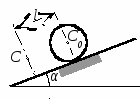 Однородное тонкое кольцо радиуса R скатывается без скольжения по наклонной плоскости из состояния покоя. Центр кольца, пройдя расстояние 14. Ременная передача начинает движение из состояния покоя под действием постоянного момента пары сил М = 2,5 Нм. Моменты инерции шкивов относительно их осей вращения I2 = 2I1 = 1 кг м2. Определить угловую скорость шкива 1 после трех оборотов, если радиусы шкивов R2 = 2R1 . 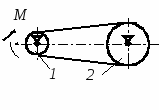 15. 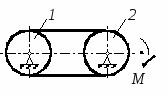 Движение шкива 2 ременной передачи начинается из состояния покоя под действием постоянного момента М = 0,5 Нм. Движение шкива 2 ременной передачи начинается из состояния покоя под действием постоянного момента М = 0,5 Нм.После трех оборотов одинаковые по массе и размерам шкивы 1 и 2 имеют угловую скорость 2 с-1. Определить момент инерции одного шкива относительно оси вращения. Применение принципа Даламбера. 1. 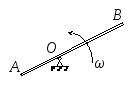 Тонкий однородный стержень AB(AO=l1, OB=l2) массой m=1 кг вращается с постоянной угловой скоростью ω =5 с-1 вокруг оси, перпендикулярной стержню. Определить модуль главного вектора сил инерции стержня, если размеры l1 = 0,2 м, l2 = 0,4 м. Тонкий однородный стержень AB(AO=l1, OB=l2) массой m=1 кг вращается с постоянной угловой скоростью ω =5 с-1 вокруг оси, перпендикулярной стержню. Определить модуль главного вектора сил инерции стержня, если размеры l1 = 0,2 м, l2 = 0,4 м.2. 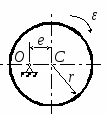 Определить главный момент сил инерции однородного диска радиуса r = 0,2 м массой m= 2 кг относительно оси вращения О, смещенной на расстояние e= 0,1 м от центра масс С. Диск вращается равноускоренно с угловым ускорением ε = 10 с-2. 3. 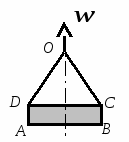 Строительную деталь массой m= 600 кг поднимают с ускорением w =1,5 м/c2. 4. Два одинаковых тела с массой 1 кг каждый соединены между собой нитью и движутся по горизонтальной плоскости под действием силы F=40 Н. Коэффициент трения скольжения тел по плоскости f= 0,1. Определить натяжение нити. 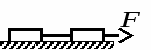 5. Два тела с одинаковыми массами m1 = m2 = 1 кг соединены стержнем и движутся по горизонтальной направляющей под действием сил F1 = 3 кН и F2 = 12 кН. Коэффициент трения скольжения тел по плоскости f= 0,2. Определить усилие в стержне. 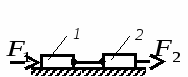 6. 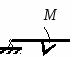 Однородный стержень длиной l = 0,6 м начинает вращаться в горизонтальной плоскости из состояния покоя под действием пары сил с моментом М = 40 Нм. Определить модуль силы реакции шарнира в начальный момент движения. Однородный стержень длиной l = 0,6 м начинает вращаться в горизонтальной плоскости из состояния покоя под действием пары сил с моментом М = 40 Нм. Определить модуль силы реакции шарнира в начальный момент движения.7. Три одинаковых груза массы mкаждый связаны нерастяжимыми гибкими нитями по схеме, приведенной на рисунке. Пренебрегая трением, а также массой блока и нитей, определить усилие в нити, соединяющей первый и второй грузы. 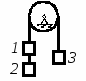 8. Груз М1массой m1 находится на шероховатой горизонтальной плоскости. К нему прикреплена нерастяжимая нить, перекинутая через идеальный блок А, на другом конце которой прикреплен груз М2массой m2. Пренебрегая массой блока и нити, определить коэффициент трения f груза М1 о плоскость, если грузы движутся с ускорением, равным по величинеw. 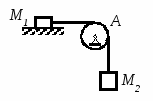 Применение принципа возможный перемещений. 1. На клин 3 действует сила F = 100 Н. Определить с какой силой толкатель 2 прижимает деталь 1 к опорной плоскости в положении равновесия, если угол α =110. 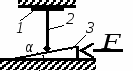 2 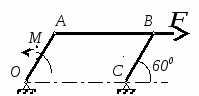 . . К шатуну АВ шарнирного параллелограмма ОАВС приложена горизонтальная сила F= 50 Н. Определить модуль момента М пары сил, которую необходимо приложить к кривошипу ОА длиной 10 см, для того, чтобы уравновесить механизм. 3. 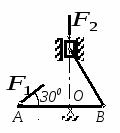 Определить модуль силы F1, которую необходимо приложить к кривошипу АВ, для того, чтобы механизм находился в равновесии, если сила F2 = 100 Н и расстояние ОА = 2 ОВ. 4. Определить модуль момента М пары сил, который необходимо приложить к шкиву 3 для равномерного подъема груза 1 весом 900 Н. Радиусы шкивов 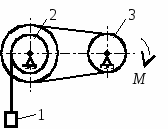 5. 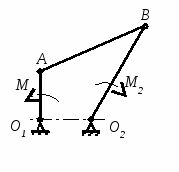 К коромыслу О1А четырехзвенного механизма приложен вращающий момент М1. Определить момент М2, передаваемый на коромысло О2В, в положении механизма, изображенном на рисунке, если О1А = 6 см, О1О2 = Применение общего уравнения динамики. 1. 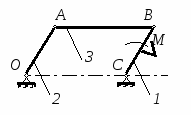 Пара сил с постоянным моментом М =0,8 Нм приводит в движение механизм, расположенный в горизонтальной плоскости. Кривошипы 1 и 2 – однородные стержни длиной l = 0,2 м и массой m1 =m2 = 1 кг, масса m3 = 2 кг. Определить угловое ускорение кривошипа 1. 2. 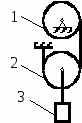 Тела 1 и 2 – однородные диски, массы и радиусы которых одинаковы. Определить ускорение тела 3, если его масса m3 = m1 = m2. 3. 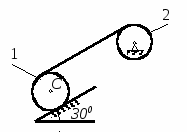 Определить ускорение центра С оси катка 1, если тела 1 и 2 – однородные сплошные цилиндры с одинаковыми массами и радиусами. 4. 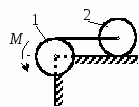 Определить угловое ускорение барабана 1 , если к нему приложена пара сил с постоянным моментом М = 0,2 Нм, массы тел m1 = m2 = 1 кг, моменты инерции относительно центральных осей I1 = I2 = 0,02 кг м2, радиусы r1= r2= 0,2 м. 5. Система состоит из подвижного и неподвижного блоков одинаковой массы m и радиуса r и связывающего эти блоки нерастяжимого невесомого каната. Пренебрегая трением, определить, какой вращающий момент Мвр необходимо приложить к неподвижному блоку, чтобы обеспечить подъем подвижного блока с заданным ускорением w. Блоки считать однородными круглыми дисками. 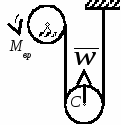 6. На трех сплошных однородных валах, к каждому из которых приложен вращающий момент М, находится балка массой m2. Определить ускорение балки, если масса каждого вала равна m1, а радиус равен r, считая, что между валами и балкой скольжение отсутствует. Трением в осях пренебречь. 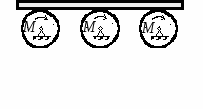 7. Два сплошных однородных вала 1 и 2 массамиm1 иm2 вращаются без трения около параллельных осей при помощи бесконечного ремня так, что скольжение отсутствует. К первому валу приложен вращающий момент М, а на второй вал наматывается трос, к концу которого привязан груз массойm3. Определить ускорение груза. Радиус вала 1 равен r. 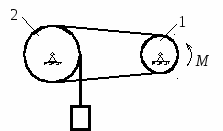 8. 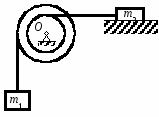 Момент инерции жестко скрепленных между собой шкивов, насаженных на общую ось, равен I =0,3 кг м2, а их радиусы r1 = 0,2 м; r2 = 0,1 м. Груз массы m1 = 1 кг падает отвесно и сообщает вращение шкивам; при этом второй груз такой же массы скользит по шероховатой горизонтальной плоскости. Определить коэффициент трения скольжения f этого груза по плоскости, если ускорение падающего груза w1 = 0,1 g. Применение уравнений Лагранжа второго рода. 1. Физический маятник состоит из однородного прямолинейного стержня ОА длины L и закрепленного на свободном конце точечного груза А. Пренебрегая сопротивлениями, определить обобщенную силу Qφ, соответствующую углу φ отклонения маятника от положения его устойчивого равновесия, если веса стержня и груза одинаковы и равны Р. 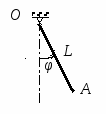 2 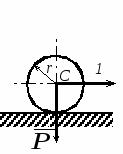 . . Колесо веса Р радиуса r катится по горизонтальной плоскости без проскальзывания под действием горизонтальной силы 3. 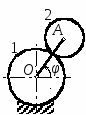 Эпициклический механизм состоит из неподвижного зубчатого колеса 1, кривошипа ОА массы 3m и длины l и подвижного колеса 2 массы m. Выбирая в качестве обобщенной координаты угол поворота φ кривошипа ОА, определить коэффициент инерции механизма. Колесо 2 считать однородным сплошным диском. 4.  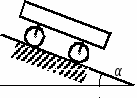 Тележка скатывается без скольжения по наклонной плоскости, образующей с горизонтом угол α. Масса тележки без колес равна М, масса всех колес - m. Считая колеса однородными сплошными дисками, определить ускорение тележки. Трением качения, а также трением в осях пренебречь. Для решения использовать уравнения Лагранжа второго рода. Тележка скатывается без скольжения по наклонной плоскости, образующей с горизонтом угол α. Масса тележки без колес равна М, масса всех колес - m. Считая колеса однородными сплошными дисками, определить ускорение тележки. Трением качения, а также трением в осях пренебречь. Для решения использовать уравнения Лагранжа второго рода.5. 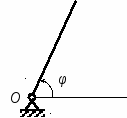 Однородный стержень длиной l = 3 м и массой m = 30 кг вращается в вертикальной плоскости. Определить обобщенную силу, соответствующую обобщенной координате φ, в момент времени, когда угол φ = 45°. 6. 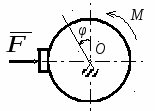 К цилиндру радиуса R, который вращается под действием пары сил с моментом М = 20 Нм, прижимается тормозная колодка силой F = 100 Н. Определить обобщенную силу, соответствующую углу φ поворота тела. Коэффициент трения скольжения колодки о цилиндр f = 0,1. 7. 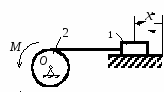 Тело 1 массой m = 30 кг и цилиндр 2 радиуса R = 0,25 м соединены нерастяжимым тросом. Определить обобщенную силу, соответствующую обобщенной координате x, если коэффициент трения скольжения между телом 1 и поверхностью f = 0,2, а к цилиндру приложена пара сил с моментом М = 25 Нм. 8. 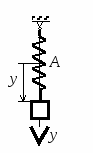 Груз массой m = 6 кг подвешен на пружине, при деформации которой возникает восстанавливающая сила F = -300 y. Определить координату y, при которой обобщенная сила Qy равна нулю. Точка А является концом пружины в недеформированном состоянии. 9. 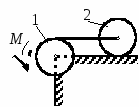 Определить угловое ускорение катка 2, катящегося без скольжения, если на блок 1 действует пара сил с моментом М = 0,6 Нм. Каток 2 считать однородным цилиндром массы m = 4 кг. Радиусы тел 1 и 2 равны r = 0,5 м. Материальная точка М массой m = 1 кг равномерно движется по окружности со скоростью v = 4 м/c. Определить модуль импульса равнодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2. |
