СОЧ по геометрии 10 кл ЕМН. соч ПО ГЕОМЕТРИИ 4 ЧЕТВ емн. Суммативное оценивание по геометрии
 Скачать 26.53 Kb. Скачать 26.53 Kb.
|
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ПО ГЕОМЕТРИИ ЗА 4 ЧЕТВЕРТЬ (ЕМН, 10 КЛАСС) Фамилия, имя _________________________________________________Класс: 10Д 1 вариант
Скалярный квадрат вектора равен 50. Найдите модуль этого вектора. Точки А(1; -2; 4), В(3; 6; 3), С(5; -2; 1), Д(3; 6; 2) являются вершинами параллелограмма АВСД. Найдите угол параллелограмма. а) Напишите уравнение сферы с центром в начале координат, если плоскость х=6 касается этой сферы. б) Сфера задана уравнением х2 + y2 + z2 -4x + 2y - 6z - 2=0 . Найдите координаты центра сферы и ее радиус. а) даны векторы 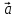 (4; -1; 5), (4; -1; 5), 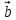 (-2; 2; 2). Верно ли, что векторы перпендикулярны? (-2; 2; 2). Верно ли, что векторы перпендикулярны? б) Даны векторы 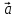 (1; 3p; 2q) , (1; 3p; 2q) , 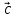 (-(9p2 +4q2); 3p; 2q), где p и q – некоторые постоянные. Покажите, что векторы (-(9p2 +4q2); 3p; 2q), где p и q – некоторые постоянные. Покажите, что векторы 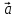 и и 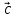 перпендикулярны для всех ненулевых значений p и q. перпендикулярны для всех ненулевых значений p и q. а) Прямая задана уравнением 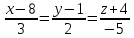 . Задайте прямую параметрически. . Задайте прямую параметрически. б) Даны прямая m и ее направляющий вектор 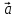 (2; - (2; -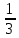 ; ; 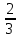 ). Точка М( 9; -5; 1) принадлежит прямой m. ). Точка М( 9; -5; 1) принадлежит прямой m. i) Напишите каноническое уравнение прямой m ii) Напишите параметрическое уравнение прямой m Дано: ( 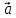 - -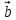 ) ) 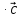 =0, ( =0, (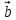 - - 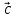 ) )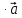 = 0. Докажите, что ( = 0. Докажите, что (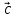 - - 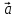 ) )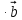 =0. =0. СУММАТИВНОЕ ОЦЕНИВАНИЕ ПО ГЕОМЕТРИИ ЗА 4 ЧЕТВЕРТЬ (ЕМН, 10 КЛАСС) Фамилия, имя _________________________________________________Класс: 10Д 2 вариант
Скалярный квадрат вектора равен 72 . Найдите модуль этого вектора. Точки А(1; 3; -3), В(1; 1; -3), С(-1; -4; 4), Д(-1; -2; 4) являются вершинами параллелограмма АВСД. Найдите угол параллелограмма. а) Напишите уравнение сферы с центром в начале координат, если плоскость х=7 касается этой сферы. б) Сфера задана уравнением х2 + y2 + z2 -6x -2y +4z - 2=0 . Найдите координаты центра сферы и ее радиус. а) даны векторы 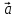 (4; -5; 6), (4; -5; 6), 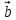 (1; 2; -4). Верно ли, что векторы перпендикулярны? (1; 2; -4). Верно ли, что векторы перпендикулярны? б) При каком значении z векторы 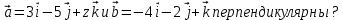 а) Прямая задана уравнением 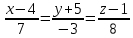 . Задайте прямую параметрически. . Задайте прямую параметрически. б) Даны прямая m и ее направляющий вектор 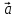 (5; (5; 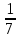 ; - ; - 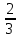 ). Точка М( 10; -4; 1) принадлежит прямой m. ). Точка М( 10; -4; 1) принадлежит прямой m. i) Напишите каноническое уравнение прямой m ii) Напишите параметрическое уравнение прямой m Дано: ( 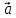 - -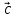 ) ) 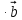 =0, ( =0, (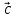 - - 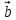 ) )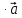 = 0. Докажите, что ( = 0. Докажите, что (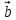 - - 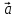 ) )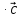 =0. =0. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
