Матем задачи в энергетике. ПР№1 Решение. Свеженцева Ольга Владимировна фио преподавателя Иркутск, 2020 г. Практическое занятие
 Скачать 35.43 Kb. Скачать 35.43 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «ИРКУТСКТЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Заочно-вечерний институт Кафедра электроснабжения и электротехники Практическая работа №1 по «Математические задачи в электроэнергетики» Вариант №14 Выполнил(а): Студент 2 курса группы ЭПбз-18-2 Зачетная книжка № 18151134 Кузьмин Антон Юрьевич (ФИО студента) Проверил(а) преподаватель: Кандидат технических наук, доцент (ученое звание и степень) Свеженцева Ольга Владимировна ФИО преподавателя Иркутск, 2020 г. Практическое занятие №1 Тема: Три формы представления комплексного числа. Действия над комплексными числами. Применение комплексных чисел в электротехнике Цель занятия: Усвоить формы представления комплексных чисел, уяснить как производятся действия над комплексными числами. Задание на занятие: Для схемы, представленной на рисунке составить систему линейных алгебраических уравнений с комплексными коэффициентами по методу контурных токов. Считать направления тока в контурах по часовой стрелке. Решить систему методом обратной матрицы или методом Крамера (определителей) и найти токи в контурах.
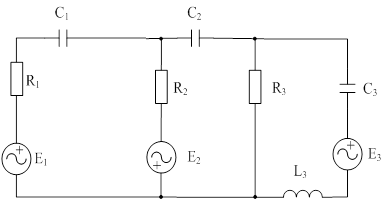 Рис 1. Переведем исходные данные согласно международной системе СИ (микрофарады в фарады, миллигенри в генри). 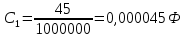 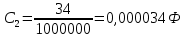 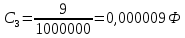 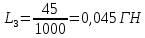 Выберем направления контурных токов I11, I22иI33 по часовой стрелке. Запишем в общем виде уравнения для контурных токов. 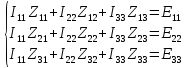 Здесь - 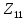 собственное сопротивление первого контура, состоит из емкостного сопротивления и двух активных сопротивлений, соединенных последовательно. Комплекс емкостного сопротивления вычисляется по формуле: собственное сопротивление первого контура, состоит из емкостного сопротивления и двух активных сопротивлений, соединенных последовательно. Комплекс емкостного сопротивления вычисляется по формуле: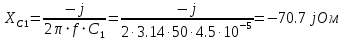 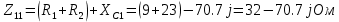 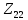 - собственное сопротивление второго контура, состоит из емкостного сопротивления и двух активных сопротивлений, соединенных последовательно. Комплекс индуктивного сопротивления вычисляется по формуле: - собственное сопротивление второго контура, состоит из емкостного сопротивления и двух активных сопротивлений, соединенных последовательно. Комплекс индуктивного сопротивления вычисляется по формуле: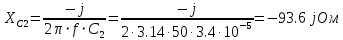 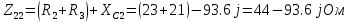 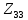 - собственное сопротивление третьего контура, состоит из индуктивного сопротивления, активного сопротивления и емкостного сопротивления, соединенных последовательно. Комплекс емкостного сопротивления и индуктивного сопротивления вычисляется по формулам: - собственное сопротивление третьего контура, состоит из индуктивного сопротивления, активного сопротивления и емкостного сопротивления, соединенных последовательно. Комплекс емкостного сопротивления и индуктивного сопротивления вычисляется по формулам: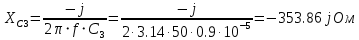 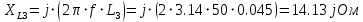 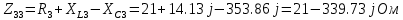 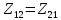 сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно) сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно)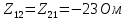 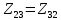 сопротивление смежной ветви между вторым и третьим контурами, взятое со сопротивление смежной ветви между вторым и третьим контурами, взятое сознаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно) 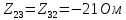 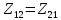 сопротивление равное 0, так ка нет смежной ветви между первым и третьим сопротивление равное 0, так ка нет смежной ветви между первым и третьимконтурами. 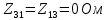 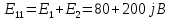 - алгебраическая сумма э.д.с. первого контура. - алгебраическая сумма э.д.с. первого контура.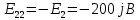 - алгебраическая сумма э.д.с. второго контура. - алгебраическая сумма э.д.с. второго контура.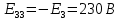 - алгебраическая сумма э.д.с. третьего контура. - алгебраическая сумма э.д.с. третьего контура.Следовательно, нахождение токов в схеме по методу контурных токов сводится к решению системы из трех линейных алгебраических уравнений с комплексными коэффициентами. 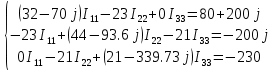 Эту систему линейных алгебраических уравнений решаем методом Крамера: Запишем основную матрицу системы 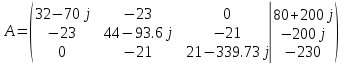 Найдем определитель: 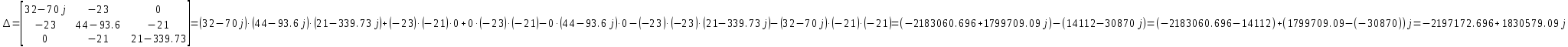 Определитель 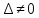 , следовательно, заданная система может быть решена методом Крамера. , следовательно, заданная система может быть решена методом Крамера.Вычислим определитель 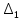 , для этого заменим первый столбец в основной матрице на столбец свободных членов B = , для этого заменим первый столбец в основной матрице на столбец свободных членов B =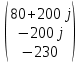 , получим: , получим: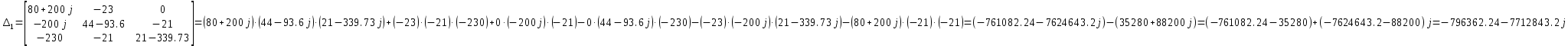 Вычислим определитель 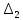 , для этого заменим второй столбец в основной матрице на столбец свободных членов B = , для этого заменим второй столбец в основной матрице на столбец свободных членов B =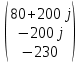 , получим: , получим: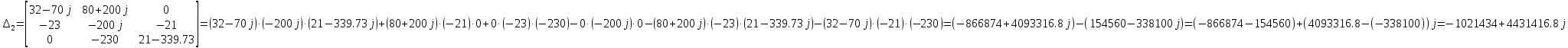 Вычислим определитель 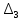 , для этого заменим третий столбец в основной матрице на столбец свободных членов B = , для этого заменим третий столбец в основной матрице на столбец свободных членов B =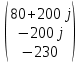 , получим: , получим: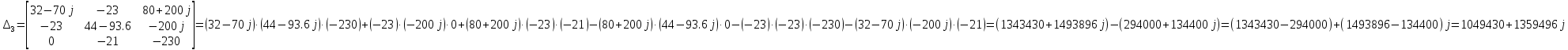 Далее по формуле Крамера находим контурные токи 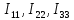 : : 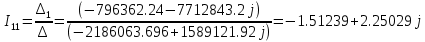 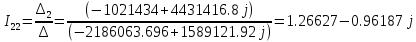 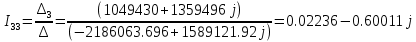 7) Проверим решение подставив значения: 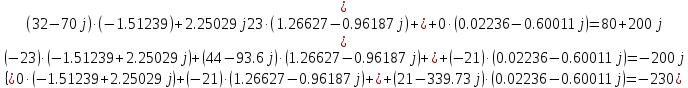 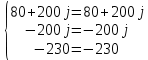 |
