модулятор. Сверхширокополосная модуляция
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
Рис.3.1 Функциональная схема квадратурного модулятораКвадратурные компоненты Квадратурные компоненты Полярная форма представления модулированного сигнала 3.3.b аппаратурно реализуется на основе управляемого автогенератора (рис.3.2). 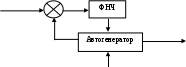 Рис. 3.2. Функциональная схема углового модулятора Сигнал от внешнего высокостабильного источника ВЧ колебания При амплитудной модуляции модулирующий сигнал просто изменяет амплитуду стабилизированного по частоте автогенератора. При угловой модуляции (общее название частотной и фазовой модуляции) амплитуда огибающей ВЧ сигнала постоянна (табл.3.1), и модуляция сводится к изменению частоты или фазы автогенератора. При частотной модуляции управляемого по частоте автогенератора комплексная огибающая При использовании для фазовой модуляции фазового модулятора (например, отрезка длинной линии с регулируемой длиной) комплексная огибающая Очевидно, что полярной и квадратурным схемам модуляции должны соответствовать и два основных способа демодуляции сигнала. Квадратурный демодулятор должен иметь функциональную схему, «зеркальную» по отношению к схеме квадратурного модулятора рис.3.1, т.к. демодулятор реализует функцию выделения комплексной огибающей из модулированного высокочастотного сигнала. Функциональная схема квадратурного демодулятора показана на рис.3.3. Предполагается, что входной модулированный ВЧ сигнал представлен в квадратурном виде: 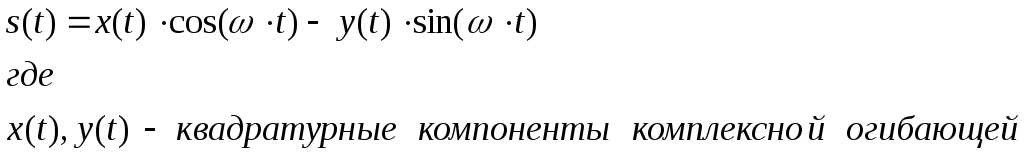 3.4 3.4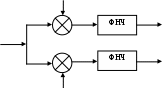 s(t) Рис.3.3. Функциональная схема квадратурного демодулятора На два перемножителя квадратурного демодулятора от внутреннего генератора поступают квадратурные компоненты опорного ВЧ колебания, которые имеют ту же самую частоту и фазу, что и несущая модулированного колебания. Сигнал на выходе каждого перемножителя равен, очевидно, произведению модулированного сигнала на соответствующую компоненту опорного сигнала: Фильтры низкой частоты удаляют из спектра сигнала на выходе перемножителя все высокочастотные компоненты. Выполняя перемножение и пренебрегая удвоенными частотами, получим: 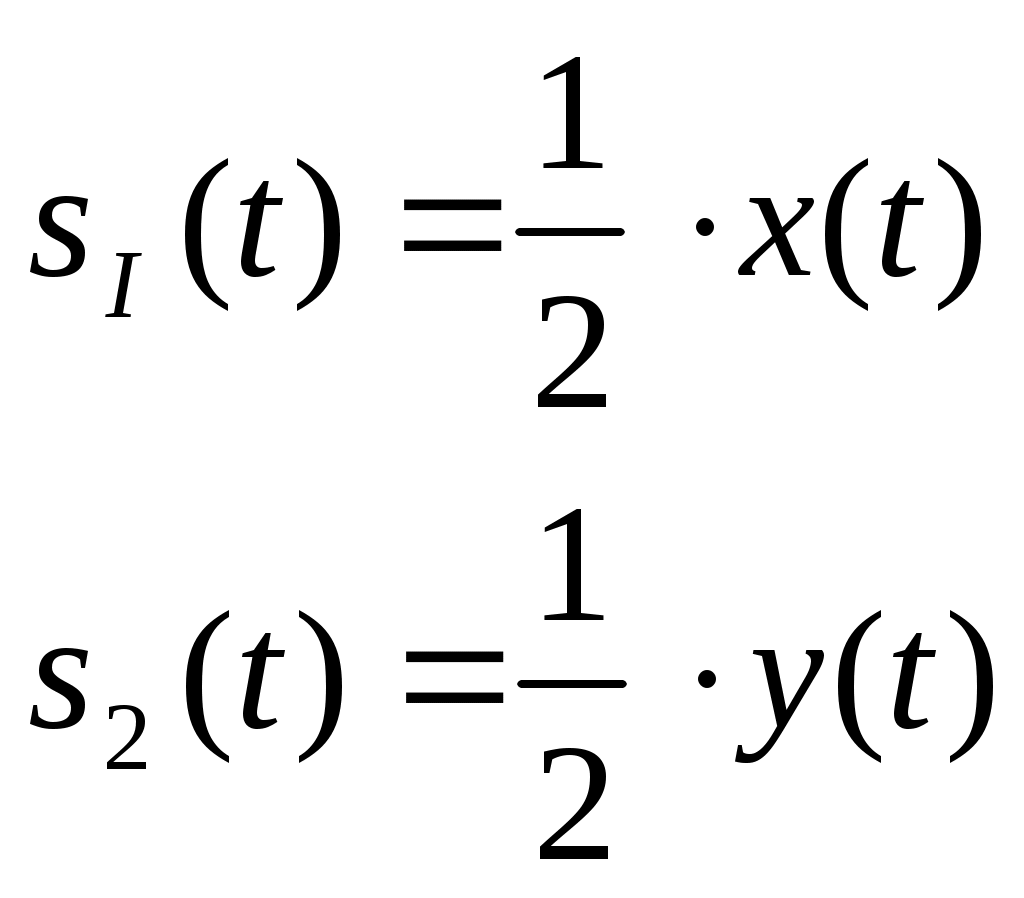 3.6 3.6Как и следовало ожидать, выходные сигналы на выходе квадратурного демодулятора равны квадратурным компонентам комплексной огибающей. Полярное представление сигнала с угловой модуляцией (частотной или фазовой) приводит к схеме демодулятора, также «зеркальной» по отношению к схеме модулятора рис.3.2 и также использующей управляемый автогенератор. Функциональная схема такого демодулятора показана на рис.3.4.  s(t) s(t) Рис.3.4 Функциональная схема демодулятора сигнала с угловой модуляцией На фазовый детектор поступают принимаемый высокочастотный модулированный сигнал Сигнал на выходе фазового детектора, по определению, пропорционален текущей разности фаз входных сигналов, т.е. модулированного сигнала и сигнала управляемого генератора: Этот сигнал, после прохождения фильтра низкой частоты (предназначенного для удаления побочных продуктов работы фазового детектора), постоянно подстраивает автогенератор под текущую принимаемую частоту сигнала в соответствии с законом изменения Приведенные в данном разделе блок-схемы схемы модуляторов и демодуляторов следует рассматривать только как функциональные, отражающие базовые, принципиальные свойства модулированных сигналов. Практическая реализация этих схем связана с решением значительных технических проблем. Так, например, для схемы рис.3.3 осуществление синхронизации опорного высокочастотного колебания Определение модулированного сигнала в частотной области В частотной области модуляция рассматривается как перенос спектра модулирующего (baseband) сигнала на высокочастотный сигнал (несущую частоту). Формально модулированный сигнал в частотной области определяется как полосовой сигнал, обладающий следующими свойствами: Сигнал существует в области частот Приведенное определение модулированного сигнала относится только к классическим узкополосным модулированным сигналам. Наличие мощности около положительной и отрицательной несущей есть отражение принятого общего подхода, при котором спектр как модулирующего, так и модулированного сигналов определяется во всем спектре частот от минус до плюс бесконечности. Для полноты картины отметим, что в принципе возможно построение модулированных сигналов, имеющих спектр только в положительной области. Это так называемые «аналитические сигналы». Специальная процедура Грэма позволяет построить аналитический сигнал из любого заданного сигнала. Однако этот круг вопросов находится вне настоящего учебного пособия. Взаимосвязь между спектром комплексной огибающей и спектром модулированного сигнала в частотной области определяется следующими фундаментальными уравнениями:  В качестве примера рассмотрим сигнал с импульсной амплитудной модуляцией. Для этой сигнала спектральная плотность комплексной огибающей Следовательно, спектральная плотность мощности модулированного сигнала равна: Ширина спектра модулированного колебания является одним из основных параметров модулированного сигнала и определяется как расстояние между первыми нулями в распределении спектральной плотности мощности слева и справа от несущей. В соответствии с формулами 3.9, 3.10 ширина спектра модулированного колебания равна ширине спектра комплексной огибающей. В частности, для импульсной амплитудной модуляции ширина спектра модулированного колебания 3.12 совпадает с шириной спектра baseband сигнала 3.11 и равна Спектральная плотность мощности модулированного колебания также характеризуется отношением энергии сигнала, заключенной в первом главном лепестке (между первыми нулями) к общей (суммарной) энергии сигнала. Этот параметр существенно зависит от вида модуляции и обычно колеблется от 80 до 99 процентов. Для приведенного выше примера импульсной амплитудной модуляции отношение мощности, заключенной в первом лепестке, к общей мощности сигнала равно 91%. Спектральное представление модулированного колебания обычно используется при анализе ширины спектра модулированного сигнала, при выборе высокочастотных и baseband фильтров. Полосовой и эквивалентный низкочастотный фильтр для модулированного сигнала В настоящем разделе рассматриваются некоторые вопросы, связанные с прохождением модулированного сигнала по линейным цепям. Важность этого вопроса определяется тем, что радиоканал, как уже отмечалось в главе 1, должен быть широкополосным и линейным для информационного цифрового сигнала. Любые нелинейные эффекты или неконтролируемые ограничения полосы частот модулирующего или модулированного сигналов приводят к межсимвольной интерференции, искажающей передаваемую информацию. И хотя модуляторы и демодуляторы являются существенно нелинейными элементами (в противном случае никакое преобразование спектра было бы невозможно), эта нелинейность имеет место по отношению к немодулированным ВЧ сигналам (несущей частоте в передатчике, опорному сигналу когерентного детектора в приемнике). По отношению же к модулирующему сигналу в передатчике или принимаемому сигналу в приемнике эти устройства остаются линейными. То же самое относится и к усилителям мощности. При усилении сигналов с амплитудной модуляцией усилители работают действительно в линейном режиме, иначе неизбежно искажение информации. Нелинейные усилители мощности могут использоваться только для специального вида модулированных сигналов (с постоянной огибающей), у которых не происходит (практически не происходит) искажений спектра передаваемого сигнала при нелинейном усилении. Таким образом, анализ прохождения модулированного сигнала по радиоканалу сводится к анализу прохождения узкополосного сигнала через линейные устройства с полосовой частотной характеристикой. Линейное устройство, как известно, полностью характеризуется своей импульсной или частотной характеристикой, которые связаны между собой прямым и обратным преобразованием Фурье. Импульсная характеристика линейного устройства с полосовой частотной характеристикой, как и сигнал в ограниченной полосе частот, формально может быть записана в виде, аналогичном 3.1: 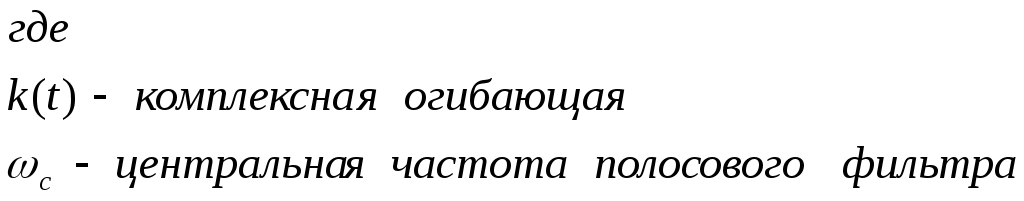 Комплексная огибающая В частотной области взаимосвязи частотной характеристики Рассмотрим теперь прохождение модулированного колебания 3.1 через полосовой фильтр, имеющий характеристики вида 3.13, 3.14 (рис.3.5.а).  Рис.3.5.а. Прохождение модулированного сигнала через полосовой фильтр  Рис.3.5.в. Прохождение модулированного сигнала через эквивалентный низкочастотный фильтр Спектр сигнала на выходе полосового фильтра равен произведению спектра входного сигнала на коэффициент передачи фильтра: 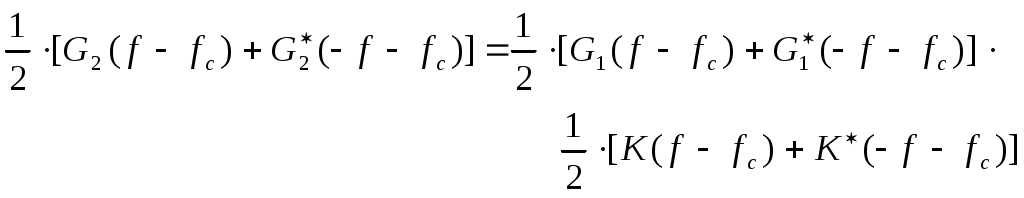 3.15 3.15Очевидно, что все произведения прямой частотной характеристики на комплексно сопряженную равны нулю, т.к. спектры этих характеристик расположены в различных областях частотной оси и не пересекаются. В результате выражение для выходного сигнала в частотной области преобразуется к виду: 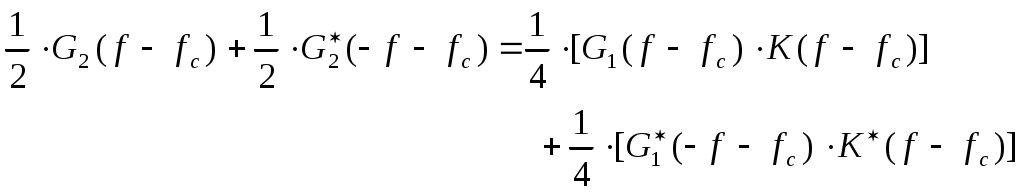 3.16 3.16Если провести преобразование Фурье от левой и правой части уравнения 3.18, то получим: Таким образом, из уравнений 3.16, 3.17 следует, что спектр комплексной огибающей выходного сигнала равен произведению спектра комплексной огибающей входного сигнала, умноженого на спектр комплексной огибающей передаточной характеристики, а во временной области выходной сигнал равен интегралу свертки от входного воздействия на комплексную огибающую (импульсную характеристику) линейного устройства. Другими словами, анализ прохождения высокочастотного модулированного сигнала, спектр которого сосредоточен в узкой полосе около несущей, можно проводить в baseband диапазоне, заменяя сам сигнал и полосовой фильтр соответствующими комплексными огибающими (рис.3.5.в). Уравнения, описывающие эквивалентный низкочастотный фильтр обычно значительно проще уравнений ВЧ полосовых фильтров. Особенно это важно при компьютерных расчетах, точность которых существенно ограничивается известной проблемой большого разброса постоянных времени. Разумеется, полученный результат относится не только к полосовым фильтрам. но и любыми линейными ВЧ устройствам. частотная характеристика которых сосредоточена вблизи несущей частоты и которые, соответственно. могут быть описаны характеристиками вида 3.13 или 3.14. Энергия модулированного сигнала и расстояние между символами модулированного сигнала Энергия одного передаваемого символа модулированного колебания определяется на основании формулы временного представления модулированного сигнала 3.1 следующим образом: 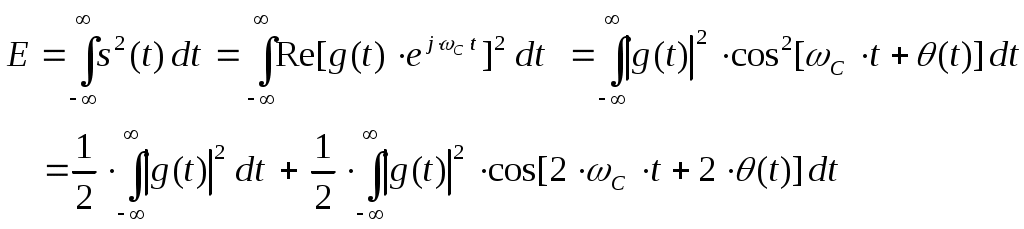 3.18 3.18Вторым интегралом в 3.18 можно пренебречь, т.к. вклад знакопеременной суммы будет незначительным в интеграл от положительной функции Взаимная энергия двух передаваемых символов модулированного колебания определяется следующим образом: 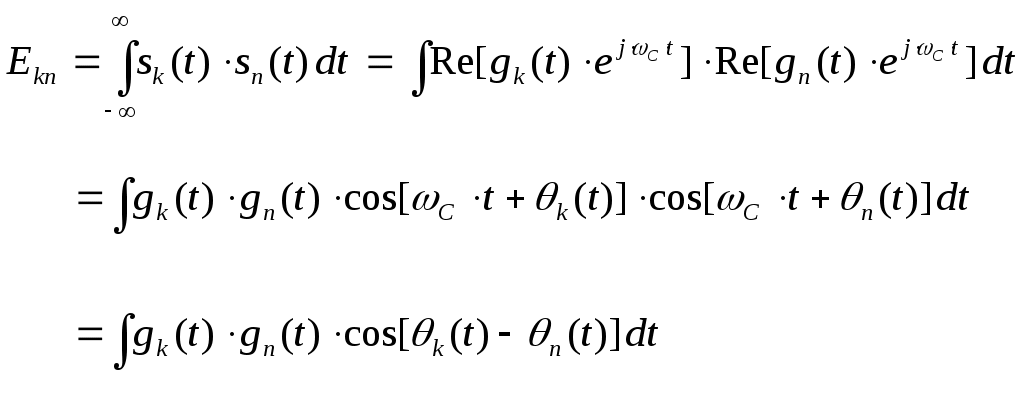 3.20 3.20При выводе 3.20, как и ранее, пренебрегаем вкладом высокочастотной компоненты в общую энергию сигнала. Одним из существенных параметров модулированного сигнала является расстояние между символами модулированного сигнала. Расстояние между символами модулированного сигнала можно рассматривать как некоторый энергетический параметр, который характеризует отношение собственной энергии передаваемого символов к их взаимной энергии, взаимосвязь или независимость передаваемых символов. Расстояние между символами характеризует их различимость при приеме сигналов. Совершенно очевидно, что, например, при передаче бинарного цифрового сигнала с помощью частотной модуляции достоверность приема сигналов возрастает с увеличением разности частот, соответствующих передаваемому нулю и единице. С увеличением разности передаваемых частот соответственно возрастает разность амплитуд сигнала на выходе частотного детектора, что и облегчает принятие решения о том, какая именно частота принята. Точно также при фазовой модуляции различимость сигналов возрастает с увеличением разности фаз несущей, соответствующей передаваемым нулю и единице. Однако понятие расстояния между сигналами значительно более общее, чем просто оценка разности амплитуд, соответствующих передаваемым символам, поскольку включает в себя еще и свойства способа модуляции. Получим строгое математическое выражение для расстояния между передаваемыми символами модулированного сигнала. Полагаем, что модулированный сигнал представлен в виде 3.1: 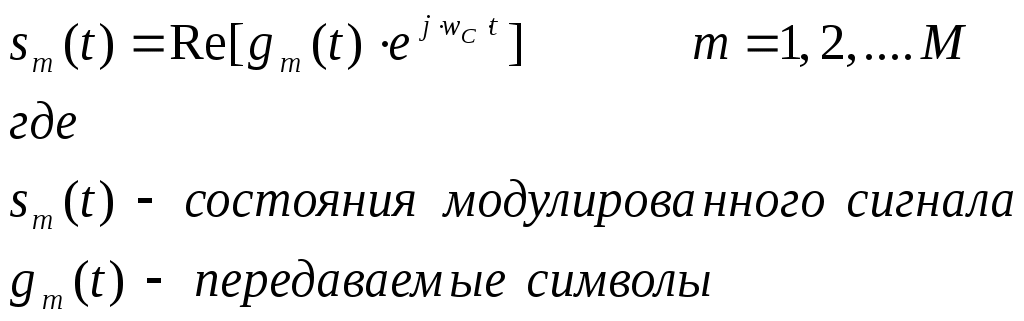 3.21 3.21Энергия каждого передаваемого символа, в соответствии с 3.19, равна: Подобным же образом можно определить взаимную энергию любых двух различных передаваемых сигналов: Расстояние между двумя состояниями в многомерном пространстве определяется как: 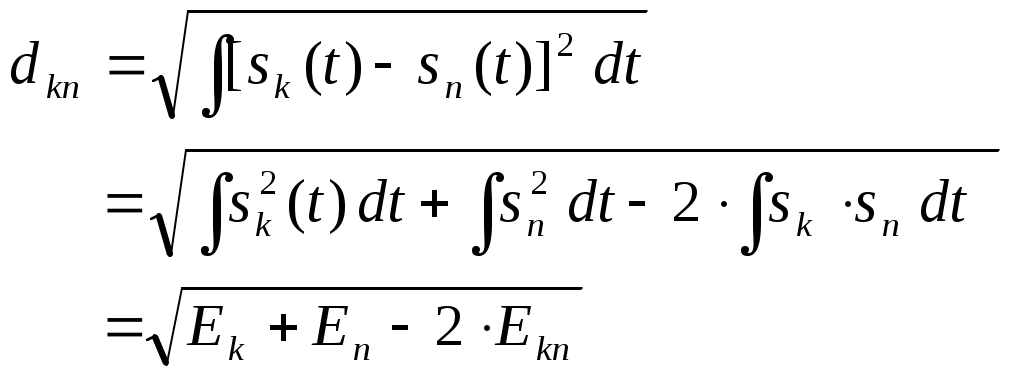 3.24 3.24В случае, если сигнал имеет равные энергии для каждого передаваемого символа, получим: Итак, расстояние между символами модулированного колебания, характеризующее потенциальную возможность различать в приемнике два разных сигнала, определяется собственной энергией, приходящейся на предаваемый символ и взаимной энергией двух символов. Отношение взаимной энергии двух сигналов в 3.24 к собственной называет кросскорреляционным коэффициентом Наилучшими характеристиками различения символов обладают сигналы с максимальным расстоянием Для прочих сигналов расстояние между символами не является постоянным, не постоянным будет и вероятность приема символов такого типа модуляции – результат будет зависеть от того, какие именно символы принимаются в текущий момент. 3.2 Импульсная амплитудная модуляция (РАМ) Импульсная амплитудная модуляция относится к классу линейной узкополосной модуляции без памяти. 3.2.1 Спектральное и временное представление импульсно модулированного сигнала Рассматривается общий случай многоуровневой импульсной амплитудной модуляция высокочастотного сигнала, при которой имеет место передача цифровой информационного сигнала 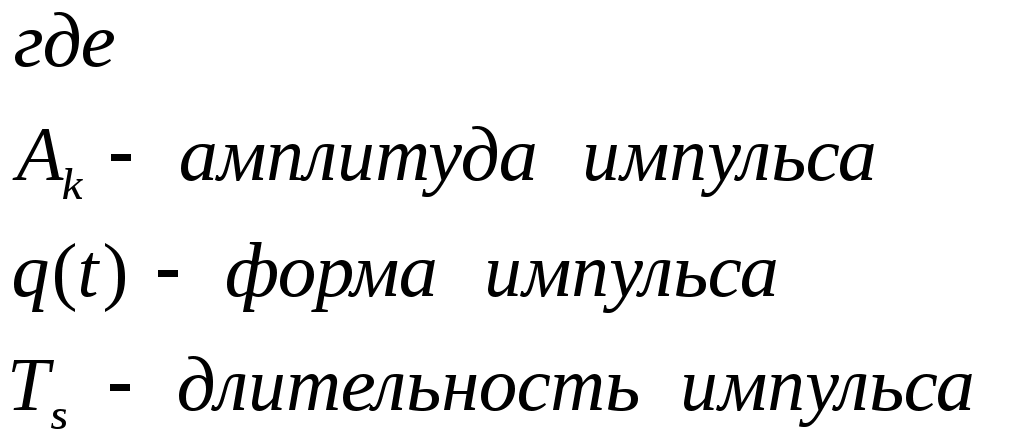 Комплексная огибающая При передаче бинарной последовательности возможные значения амплитуд импульсов Так, например, для четырехуровневого сигнала (М=4) амплитуда импульсов цифрового сигнала может принимать значения Высокочастотный импульсно модулированный сигнал Как следует из формулы 3.28, импульсно-модулированный сигнал во временной области представляет собой последовательность импульсов Спектральная плотность мощности импульсно модулированного сигнала 3.28 определяется в соответствии с общей формулой 3.11, а именно: спектральная плотность мощности модулированного сигнала в области положительных частот совпадает со спектральной плотностью мощности комплексной огибающей при замене частоты в baseband диапазоне на отклонение частоты от несущей ВЧ сигнала. Поскольку комплексная огибающая при амплитудной модуляции совпадает с модулирующим сигналом (3.26), то и спектральная плотность мощности импульсно модулированного ВЧ колебания совпадает со спектральной плотностью мощности модулирующего сигнала (для положительных частот): 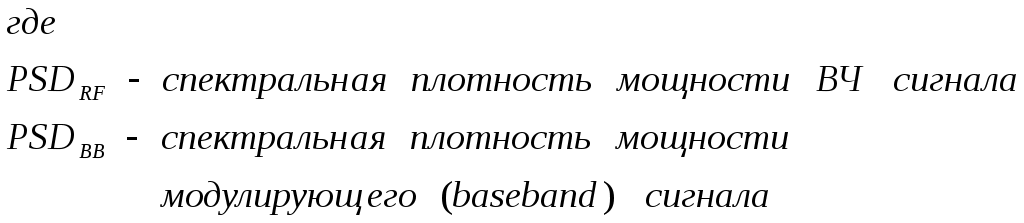 Определим спектральную плотность мощности ВЧ сигналов с импульсной амплитудной модуляцией для различного вида модулирующих сигналов. Распределение спектральной плотности мощности вычисляется с помощью общей формулы 3.29. Простейшее распределение спектральной плотности мощности имеет высокочастотный РАМ сигнал, для модуляции которого используется бинарный полярный NRZ сигнал с импульсами прямоугольной формы. Подставляя в 3.29 выражение 2.28, получим: Форма импульсов бинарного модулирующего сигнала может быть не только прямоугольной. Рассмотрим для примера полярный бинарный сигнал с синтезированной формой импульсов вида: Информационная единица передается косинусоидальным импульсом положительной полярности, информационный ноль – импульсом отрицательной полярности. Как и прямоугольный, косинусоидальный импульс определен на символьном интервале длительностью Спектральная плотность мощности псевдослучайного полярного NRZ сигнала с такой формой импульса равна: Спектральная плотность мощности импульсно модулированного сигнала совпадает с 3.32 при замене частоты Распределение мощности в спектре РАМ сигнала для прямоугольного и косинусоидального импульсов бинарного полярного модулирующего сигнала в зависимости от нормированной частоты 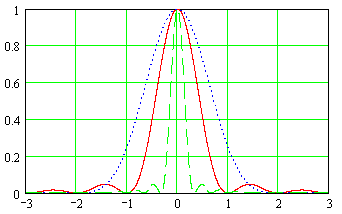    Рис.3.6 Спектральная плотность мощности РАМ сигнала До сих пор в качестве модулирующего сигнала рассматривался полярный NRZ сигнал, в котором нули и единицы цифровой последовательности кодируются положительной или отрицательной амплитудой модулирующего сигнала. Такой модулирующий сигнал, очевидно, не содержит постоянной составляющей в baseband диапазоне и, соответственно, модулированный сигнал не содержит в своем спектре несущей частоты. При использовании униполярного модулирующего сигнала его спектральная плотность мощности в baseband диапазоне будет содержать Как следует из 3.33, наличие Спектральная плотность мощности РАМ сигнала при использовании многоуровневого модулирующего сигнала также вычисляется по формуле 3.28 при использовании символьного временного интервала TS вместо битового интервала Tb. В разделе, посвященном baseband сигналам, было показано, что символьный интервал М-уровневого сигнала в Расстояние между символами РАМ сигнала Расстояние между символами модулированного сигнал, как уже отмечалось ранее, характеризует «различимость» сигналов при приеме. В дальнейшем этот параметр будет использован для вычисления достоверности приема импульсно модулированного сигнала. Для РАМ сигналов в соответствии с общей формулой для расстояния между сигналами 3.26 и формулами для собственно и взаимной энергиями: 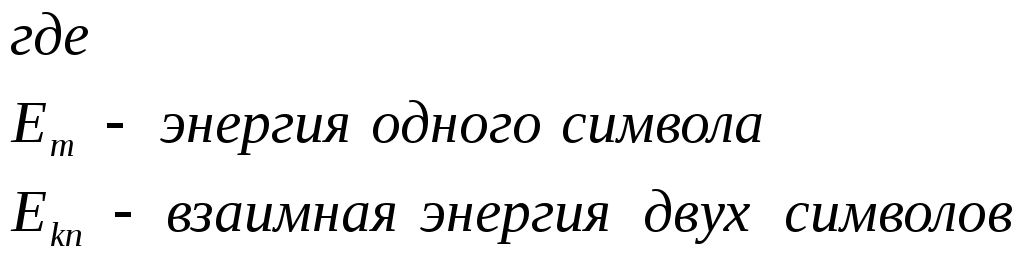 Вычислим собственную и взаимную энергии для символов РАМ сигнала. Энергия сигналов РАМ в соответствии с 3.23 равна: 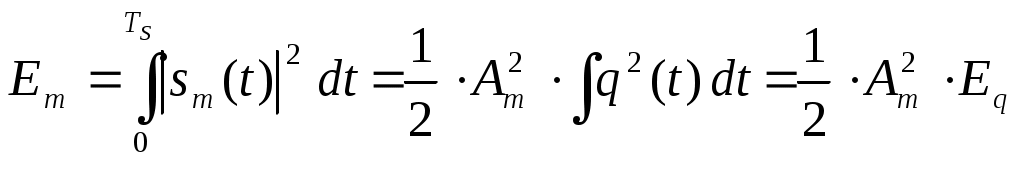 3.36 3.36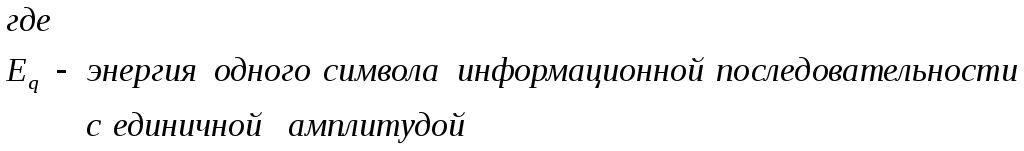 Взаимная энергия двух сигналов РАМ в соответствии с 3.24 равна: 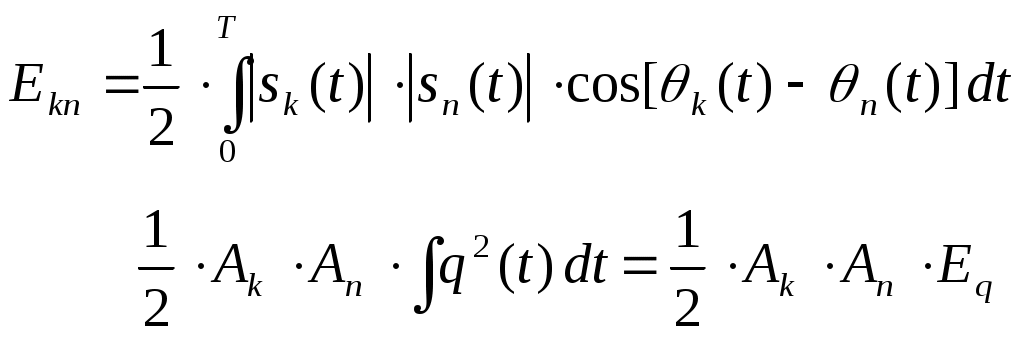 3.37 3.37В формуле 3.37 учтено, что комплексная огибающая РАМ сигнала g(t) действительная функция времени и фазовый сдвиг между символами равен 0. Подставляя 3.36 и 3.37 в выражение для расстояния между сигналами 3.35, получим: Очевидно, что минимальное расстояние между сигналами имеет место при Для импульса прямоугольной формы Модуляторы и демодуляторы РАМ сигнала Модулятор РАМ, реализующий функцию 3.28, имеет тривиальную структуру и функционально представляет собой многопозиционный ключ, изменяющий амплитуду несущей частоты в соответствии с амплитудой модулирующего сигнала. Практически РАМ сигнал с произвольной формой импульса генерируется ЦАП (цифро-аналоговым преобразователем), работающим под управлением baseband процессора. Некогерентный демодулятор РАМ сигнала представляет собой обычный амплитудный детектор огибающей сигнала. Восстановление комплексной огибающей РАМ сигнала в приемнике можно показать на примере простейшего некогерентного АМ детектора с квадратичной характеристикой. Полный сигнал на выходе детектора, с учетом 3.28, очевидно равен: 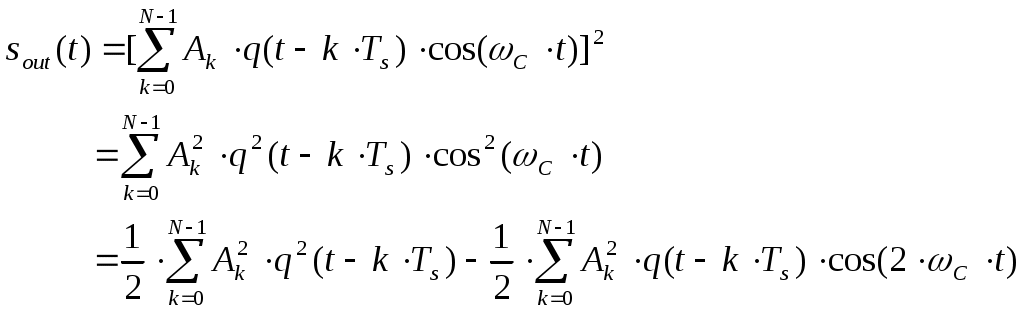 3.40 3.40Как следует из 3.40, выходной сигнал некогерентного детектора с квадратичной характеристикой представляет собой сумму квадратов амплитуд импульсов, спектр которых расположен в baseband диапазоне, и те же самые импульсы, заполненные высокочастотным сигналом с удвоенной частотой. Высокочастотные компоненты удаляются из выходного сигнала с помощью фильтра низкой частоты. Если исходный модулирующий сигнал является униполярным сигналом с амплитудами импульсов, равными 0 вольт и U вольт, то демодулированный сигнал представляет собой последовательность униполярных импульсов с амплитудами 0 и U2 . Следовательно, в результате демодуляции получен исходный модулирующий сигнал с несущественными (с информационной точки зрения) искажениями. Следует отметить, что искажения формы принимаемых импульсов при использовании некогерентного детектора обязательны и неизбежны. Процесс детектирования является принципиально нелинейным процессом. В некогерентном детекторе нелинейность работы детектора достигается за счет достаточно большой величины принимаемого сигнала. Появляющийся при детектировании исходный модулирующий сигнал обязательно сопровождается появлением и других комбинационных составляющих в baseband спектре, что и приводит к искажению формы исходного сигнала. Если исходным сигналом является полярный сигнал с амплитудами U и –U, то демодулированный сигнал представляет собой просто постоянную величину U2 . Следовательно. демодуляция полярного сигнала с помощью некогерентного детектора невозможна. Точно также невозможна и демодуляция некогерентным детектором многоуровневого полярного сигнала. Приведенный пример иллюстрирует общее положение, согласно которому только сигнал, имеющий в своем спектре несущую частоту, может быть демодулирован с помощью некогерентного детектора. Когерентный детектор (рис.3.7) представляет собой вариант квадратурного демодулятора рис.3.3, который может детектировать модулирующий сигнал любой формы, в том числе и сигнал с импульсной амплитудной модуляцией.  Тактовая синхронизация Рис.3.7 Когерентный детектор Сигнал на входе детектора равен Сигнал на выходе перемножителя равен После ФНЧ сигнал на выходе когерентного детектора равен, очевидно, только первому слагаемому в 3.42 3.3 Фазовая модуляция (PM) Фазовая модуляция относится к классу узкополосной линейной модуляции без памяти (BPSK, QPSK) или с памятью (DBPSK, 3.3.1 Общее представление фазомодулированного сигнала При цифровой фазовой модуляции М возможных фазовых состояний несущей отображают М позиционный модулирующий сигнал. Общая форма записи фазомодулированного сигнала имеет вид (табл.3.1): 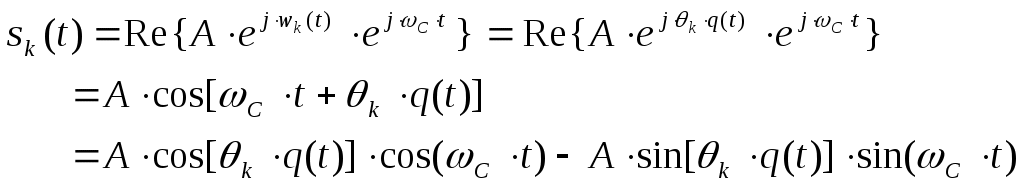 3.43 3.43 В соответствии с 3.43, фазомодулированный сигнал во временной области представляет собой синусоидальное колебание с постоянной частотой и амплитудой. Фаза колебания изменяет свое значение на каждом Определим выражение для спектральной плотности мощности фазомодулированного сигнала. В соответствии с генеральной формулой (3.9), спектральной плотность мощности модулированного сигнала определяется спектральной плотностью мощности комплексной огибающей. Комплексная огибающая фазомодулированного сигнала, в соответствии с 3.43 и табл.3.1, равна: По определению спектральная плотность мощности от реальной функции времени определяется формой этой функции на всем временном интервале от нуля до бесконечности и не зависит от фазы (начала отсчета) для рассматриваемой функции. Следовательно, спектральная плотность мощности фазомодулированного сигнала определяется синусной (или косинусной) компонентой от модулирующего сигнала в выражении 3.44: Определим расстояние между символами фазомодулированного сигнала для прямоугольной формы модулирующих импульсов на основании, как и ранее, общего выражения 3.22. Собственная энергия фазомодулированного сигнала в соответствии с 3.19 равна: Взаимная энергия двух сигналов в соответствии с 3.22 равна: 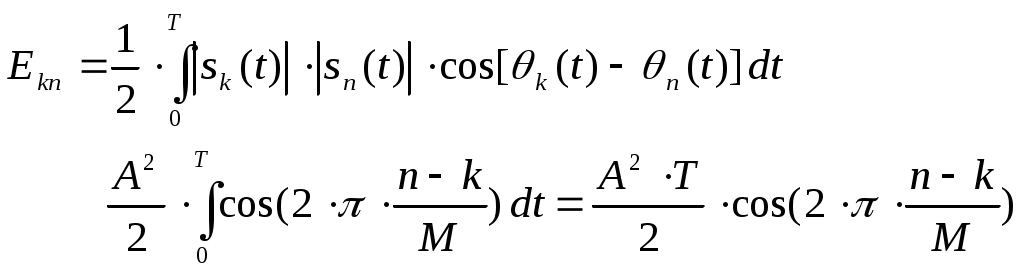 3.47 3.47Расстояние между символами фазомодулированного сигнала с учетом 3.46, 3.47 равно: 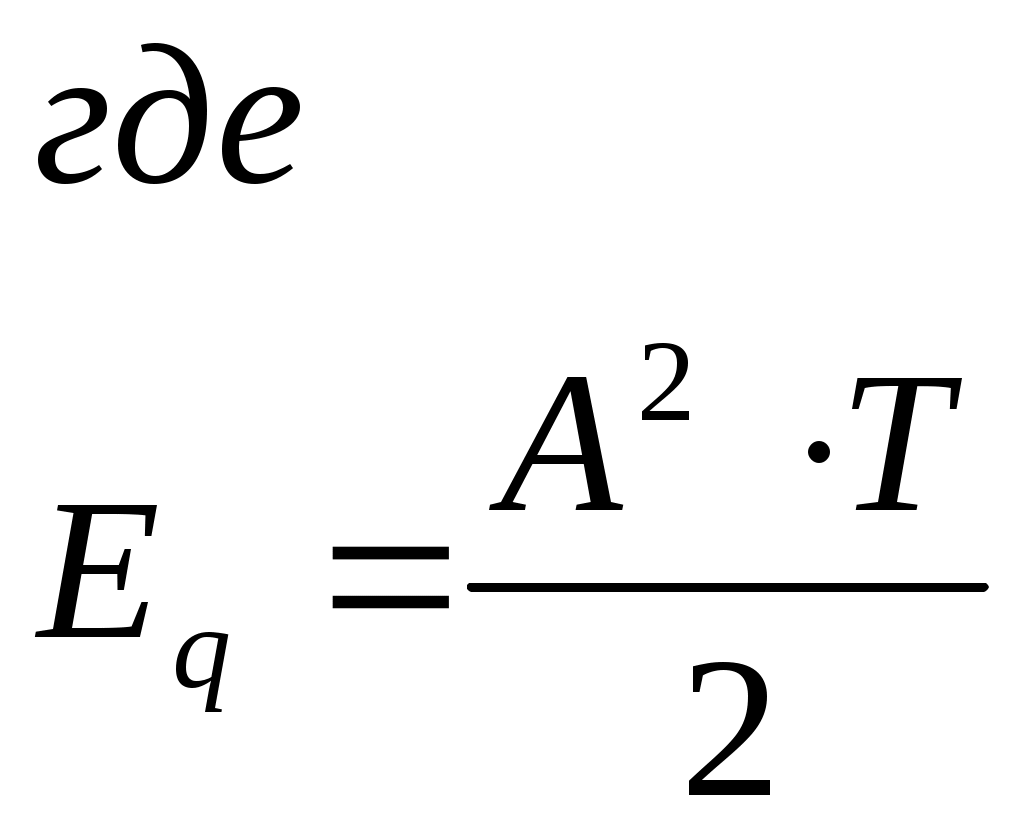 Очевидно, что минимальное расстояние между сигналами имеет место при Как и для РАМ модуляции, все символы фазомодулированного сигнала имеют равную энергия, зависящую только от амплитуды несущего колебания и длительности информационного импульса. Расстояние между символами, очевидно, уменьшается с увеличением количества уровней сигнала М. Бинарная фазовая модуляция (BPSK – Binary Phase Shift Keying)) Для двухуровневой фазовой модуляции (М=2) модулирующий сигнал может принимать два различных значения, определяемые передаваемым символом в исходной бинарной информационной последовательности. Другими словами, передаваемым информационным символам 0 или 1 соответствуют два возможных значения фазы колебания несущей частоты При подстановке этих значений в 3.44 комплексная огибающая Однако между РАМ и BPSK существует и весьма существенная разница. |
