Свойство биссектрисы угла треугольника. Свойство биссектрисы угла треугольника
 Скачать 171.5 Kb.
|
|
СВОЙСТВО БИССЕКТРИСЫ УГЛА ТРЕУГОЛЬНИКА Кочарова Карине Суреновна МОУ СОШ № 15, учитель математики (высшая категория) г. Комсомольск-на-Амуре «Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника». Данное свойство сформулировано в виде задачи № 535 учебника «Геометрия 7 – 9» авторов Л.С. Атанасяна и др. Считаю полезным запомнить это свойство как теорему. На протяжении нескольких лет аттестации учащихся в форме ЕГЭ предлагались задачи по планиметрии, которые при применении этого свойства решались бы легче. Мне хочется поделиться способом с применением данного свойства. Задача 1. В равнобедренном треугольнике АВС с основанием АС проведены две высоты ВТ и АF. Известно, что АВ = 15, АК = 5, где К – точка пересечения этих высот. Найти площадь треугольника АВК (рис. 1). Р 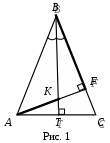 ешение. Так как ВТ высота, проведенная к основанию АС равнобедренного треугольника АВС является биссектрисой угла В, то отрезок ВК – биссектриса угла В треугольника АВF. 1) По свойству биссектрисы  , пусть  .2) Рассмотрим треугольник АВF. По теореме Пифагора  , так как  , то . .3)  ;  . Ответ:  .Задача 2. В равнобедренном треугольнике АВС с основанием АС проведены две высоты ВТ и СН, которые пересекаются в точке К. Найти площадь треугольника ВКС, если ВН = 12, НК = 4. Решение аналогично задаче 1.  – биссектриса треугольника  .Ответ:  .Задача 3. В равнобедренном треугольнике АВС с основанием АС высоты  и 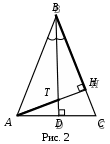АН пересекаются в точке Т, причем АТ = 10, ТН = 8. Найти площадь треугольника АВТ (рис. 2). Р  ешение. Так как высота, проведенная к основанию АС равнобедренного треугольника АВС является биссектрисой угла В, то отрезок  – биссектриса угла В треугольника  . 1) По свойству биссектрисы  , пусть  . 2) Рассмотрим треугольник . По теореме Пифагора , так как  , то  . Следовательно  .3)  , так как  .  . Ответ:  .Задача 4. Площадь равнобедренного треугольника АВС равна 90, а боковая сторона равна 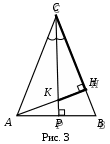 . К основанию АВ и стороне ВС проведены высоты СР и  , пересекающиеся в точке К. Найти площадь треугольника СКН (рис. 3). Р  ешение. 1)  ,  ,  .2) Из треугольника  ,  ;  .3) По теореме Пифагора  , откуда  .4) Так как  высота, проведенная к основанию  равнобедренного треугольника АВС является биссектрисой угла С, то отрезок  – биссектриса угла С треугольника . По свойству биссектрисы  , пусть  , тогда .  . ;  .Ответ:  .Задача 5. Дан ромб  с острым углом В. Площадь ромба равна  , а синус угла В равен . Высота СН пересекает диагональ ВD в точке К. Найдите длину отрезка СК (рис. 4). Решение. Так как диагональ ромба является биссектрисой угла, то 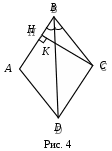– биссектриса угла В, а значит и ВК – биссектриса угла В треугольника  . Далее применяем свойство биссектрисы угла любого треугольника.О  твет:  .Замечу, что учащиеся часто находят площадь треугольника либо как разность площадей двух прямоугольных треугольников, либо по формуле Герона. Рациональнее находить, как показано в решении выше, основание и высота, проведенная к ней, на рисунке отмечены жирной линией. |