Шпоры по ТОЭ. Т рехфазной системой
 Скачать 0.82 Mb.
|
|
Метод контурных токов Метод расчета путём решения уравнений, основанных на законах Кирхгофа, рассмотренные выше, трудоёмок. Например, для цепи, имеющей шестнадцать ветвей, требуется решать систему шестнадцати уравнений. Значительно упрощают расчет методом контурных токов, так как он позволяет сократить число уравнений. При расчёте этим методом полагают, что в каждом независимом контуре схемы течёт свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Синусоидальный ток и его основные характеристики В настоящее время перем ток находит широкое применение в технике, так как он легко трансформируется и передается на большие расстояния при высоком напряжении и малых потерях. Кроме того, эл машины и другие электротехне устройства, предназн для работы в цепях перем тока, относительно просты и достаточно надежны в эксплуатации. В электротехнике наибольшее распространение получил синусоидальный перем ток, то есть ток, величина которого изменяется по закону синуса. Поэтому мгновенное значение синусоидального тока выражается формулой  , f = 1/T - частота, ω – угловая частота (выражается в рад/с или с-1 ).  . Аргумент синуса, то есть  н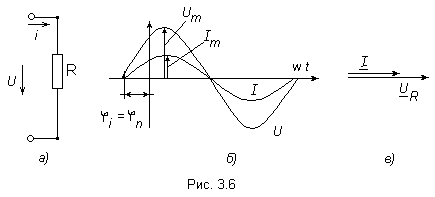азывают фазой. Фаза характ состояние колебания (его численное значение) в данный момент времени t.Л  юбая синусоидально измен функция опред тремя величинами: амплитудой, угловой частотой и начальной фазой. Если частота слишком низкая, то увел габариты эл машин и, следовательно, расход материалов на их изготовление. При больших частотах увел потери энергии в сердечниках эл машин и трансформаторах. Под средним значением синусоидально изменяющейся величины понимают её среднее значение за полпериода. Среднее значение тока: 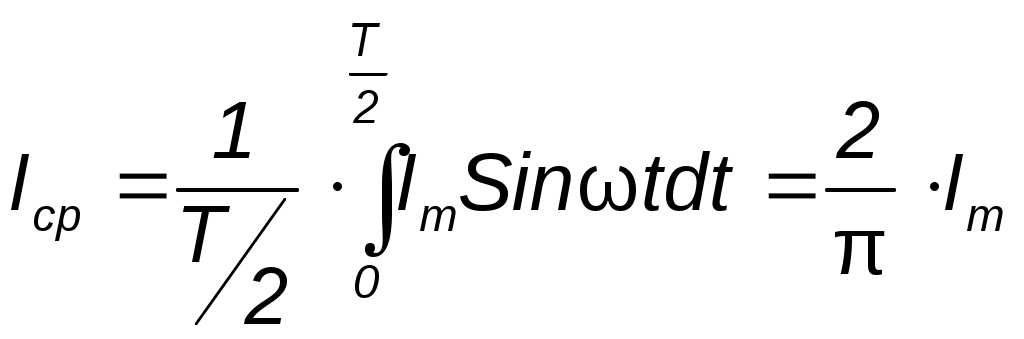 . О переменном токе всё известно, если задано его уравнение или график..Перем ток обычно характ его действующим значением 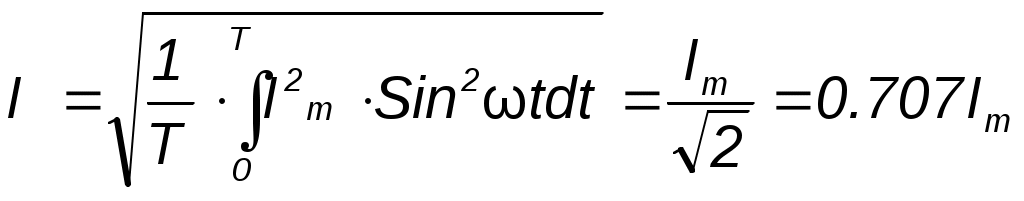  . Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного.Графическое изображение синусоидальных величин Для сравнения эл величин, изменяющихся по синусоидальному закону, необходимо знать разность их начальных фаз. Если график изменения во времени напряжения  на каком - либо участке цепи пересекает координату времени t раньше графика тока  , то говорят, что напряжение по времени опережает ток. Векторное изображение синусоидальных величин. При гарм изменении синус величины пост остаётся амплитуда. Этим можно воспользоваться для определения мгновенного значения электрической величины, не рассматривая графика её зависимости от времени. Синус функцию времени можно изобразить вектором, равным Получение синусоидальной Э.Д.С. В лин элект цепях синус ток возникает под действием синус Э.Д.С. Синус зав можно получить, вращая с пост скоростью в равномерном магн поле проводник в виде прямоугольной рамки площадью S. Тогда магнитный поток через рамку 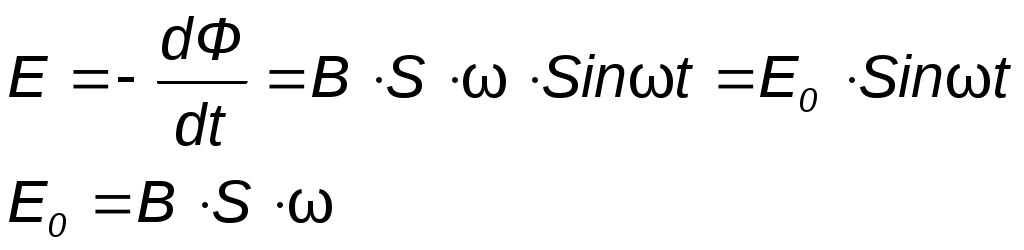 , Поскольку при равном вращении рамки угловая скорость  , то угол  будет изменяться по закону   .Так как при вращении рамки пересек её магн поток всё время меняется, то по закону электромагн индукции в ней будет наводиться Э.Д.С. индукции  Т о,возникает синус Э.Д.С., а если рамку замкнуть на нагрузку, то в цепи потечёт синус ток.Резистивный элемент В эл цепи с рез элементом R ток изменяется по синус закону с нач фазой  ,  . Напряжение на зажимах резистора  ; где  - ампл значение напр на зажимах резистора, Кривые изменения напряжения  и тока (рис. 3.6б) в один и тот же момент времени t достигают максимального значения и одновременно проходят нулевые значения. Иначе говоря, обе кривые совпадают по фазе  . кторы  и  совпадают по направлению (угол  ). Переходя к действующим значениям можно записать  ;  . Сопротивление переменному току будет больше, чем постоянному за счет неравномерного распределения тока в проводе и потерь энергии в окружающую среду. Поэтому в отличие от сопротивления постоянному току сопротивление R в цепи переменного тока называется активным. , противоположную направлению движения стрелки часов).Умножение на –j означает поворот вектора на угол –90 градусов (по часовой стрелке). амплитуде данной функции, равномерно вращ с угл скоростью ω. При этом нач положение вектора определяется (для t=0) его нач фазой  . При изобр синус Э.Д.С., напр и токов из начала координат проводят векторы, равные амплитудным значениям этих величин, под углом  к горизонтальной оси. Положительные углы откладываются против часовой стрелки.Совокупность векторов на плоскости, изображающих Э.Д.С., напряжения, токи одной частоты, называют векторной диаграммой.При иссл установившихся режимов векторы неподвижны, их длина равна действ значениям эл величин. С помощью векторов можно производить геометрическое суммирование электрических величин. Представление синусоидальных величин комплексными числами. Синус измен эл величину можно представить компл числом и изобр в виде вектора на компл плоскости с прямоугольной системой координат. Компл число состоит из действ и мнимой частей. По оси ординат откладывают мнимую часть компл числа, а ось обозначают +j; по оси абсцисс – действительную часть комплексного числа, а ось обозначают +1. На компл плоскости синус величина может изобр в виде модуля и аргумента или в виде двух сост вектора, напр по действ и мнимой осям. Н 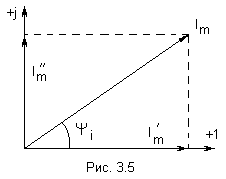 апример, синусоидальный ток  представляют вектором  , модулем которого явл знач амплитуды тока  , а аргументом нач фаза , кот можно выражать в радианах или в градусах Сост вектора по действительной оси будет  , а по мнимой -  , то есть  .При построении векторных диаграмм точно фиксируют угол сдвига между векторами, а положение их относительно осей комплексной плоскости может быть произвольным, поэтому оси можно не изображать. записанными в показательной форме:  ,где  - оператор поворота единичного вектора относительно оси действительных величин.Умножение на j означает поворот вектора на +90 градусов (в сторону Индуктивный элемент. Изменение тока в цепи с индуктивностью L вызывает возникн Э.Д.С. самоиндукции  , которая по закону Ленца противодействует измен тока. При увелич тока Э.Д.С. Дей-т навстречу току, а при умен - в направлении тока, противодействуя его измен. Для тока, измен по гарм закону  и при   Э.Д.С. самоиндукции  Чтобы в цепи протекал ток, требуется иметь на зажимах напряж, уравновеш Э.Д.С. самоиндукции, равное ей по значению и противопол по знаку  где  - амплитуда напряжения. инд сопрот и измер в Омах: . на участке цепи с индуктивностью L напряжение опережает ток на четверть периода ( ).Если R =0, то средняя активная мощн равна 0: . Емкостной элемент. В цепи с конденсатором вкл на напр перем тока, происходит непрерывное перемещение эл зарядов. М 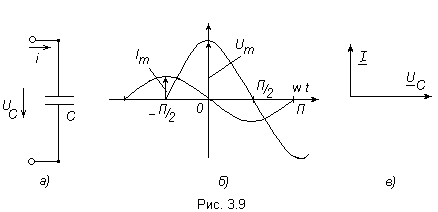 гн ток 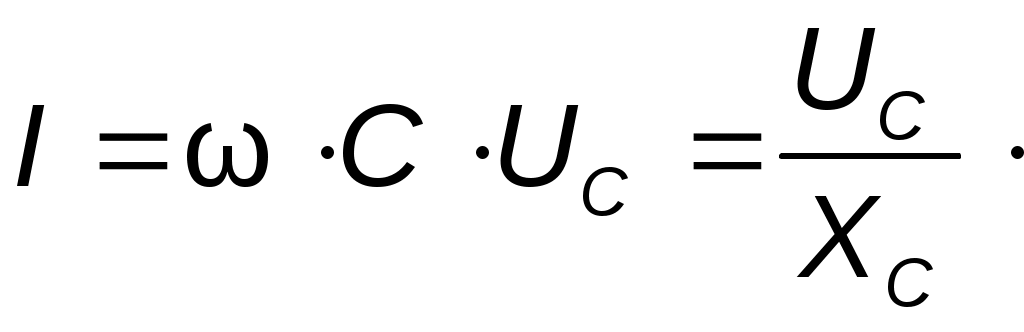 , Если напр на зажимах конденсатора изм по синусзакону: то ток в цепи  ,ёмкостным сопротивлением цепи: Емкостное сопротивление обратно пропорционально частоте приложенного напряжения  ,  Активная, реактивная и полная мощности. законы изменения тока и напряжения  ,  , то их произведение  . Мгновенная мощность  График этой функции - результат графического умножения графиков тока и напряжения. активной мощностью Р -среднее значение мгн мощности за период:  .  Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R  . Следовательно:  . Единица активной мощности - 1Вт (Ватт). Под реактивной мощностью Q принимают произведение напряжения на участке цепи на ток, протекающий по этому участку, и на синус угла φ между напряжением и током.  . Единица реактивной мощности – вольт-ампер реактивный (ВАр).Величина, объединяющая активные реактивные мощности, называется полной мощностью.  . Единица полной мощности - вольт-ампер (ВА).Для того, чтобы вычислить полную мощность нужно комплекс напряжения умножить на сопряженный комплекс тока:  .  . (3.41)мощности P, Q, S связаны следующей зависимостью:  . Графически эту связь можно представить в виде прямоугольного треугольника– треугольника мощности, у которого имеются катет, равный Р, катет равный Q и гипотенуза S. Отношение Р к S, равное  , называется коэффициентом мощности. . На практике всегда стремятся увеличить , так как реактивная мощность, которая всегда существует в цепи R, L, C, не потребляется, а используется лишь активная. Из этого можно сделать вывод, что реактивная мощность является лишней и ненужной.В общем случае резонансная частота 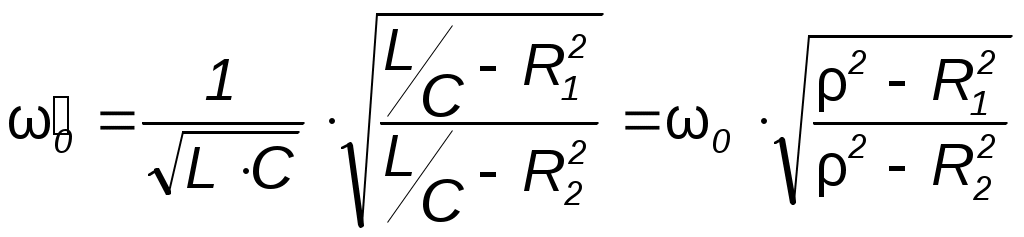  , В теоретическом случае при  токи  и  сдвинуты по фазе относительно напряжения на углы  (рис. 3.23б) и суммарный ток  . Входное сопротивление цепи при этом бесконечно велико.  резонанс возможен, если сопротивления  оба бо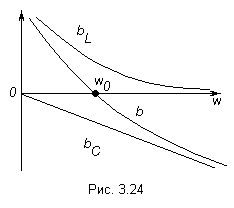льше или оба меньше ρ.Если  , то резонансная частота  имеет любое значение, то есть резонанс наблюдается на любой частоте. Н  а рис. 3.24 показаны частотные характеристики проводимостей ветвей  и  , и входной проводимости цепи  .При изменении частоты от 0 до  эквивалентная проводимость  , то есть индуктивная и изменяется от  до 0. При  наступает резонанс токов,  .При возрастании частоты от  до входная проводимость  , то есть имеет емкостной характер и изменяется от 0 до  . |