Задача. T температура тела в Кельвинах, a площадь поверхности излучения
 Скачать 16.71 Kb. Скачать 16.71 Kb.
|
|
Для решения задачи используем закон Стефана-Больцмана, который описывает излучение тепла черного тела. Формула закона Стефана-Больцмана выглядит следующим образом: 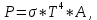 где P - мощность излучения, σ - постоянная Стефана-Больцмана ( 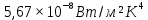 ), T - температура тела в Кельвинах, A - площадь поверхности излучения. ), T - температура тела в Кельвинах, A - площадь поверхности излучения.Переведем температуру трубки и нити в Кельвины: T1 = 700 + 273 = 973 К (температура трубки), T2 = T1 + 300 = 1273 К (температура нити). Найдем площадь поверхности нити: d = 0,1 мм = 0,0001 м (диаметр нити), 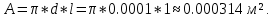 Рассчитаем мощность излучения нити и трубки: 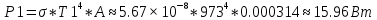 (мощность излучения трубки), (мощность излучения трубки),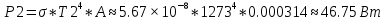 (мощность излучения нити). (мощность излучения нити).Определим мощность, которую нить должна поглотить для поддержания своей температуры на 300 К выше температуры трубки: 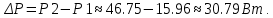 Учитывая, что мощность в электрической цепи равна 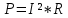 , найдем сопротивление нити: , найдем сопротивление нити: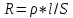 , где ρ - удельное сопротивление вольфрама, l - длина нити, S - площадь поперечного сечения нити. , где ρ - удельное сопротивление вольфрама, l - длина нити, S - площадь поперечного сечения нити.Удельное сопротивление вольфрама 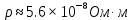 (при 20 °C). Так как зависимость сопротивления от температуры слабая, в данной задаче примем, что ρ не изменяется. (при 20 °C). Так как зависимость сопротивления от температуры слабая, в данной задаче примем, что ρ не изменяется.S = π * (d / 2)^2 = π * (0.0001 / 2)^2 ≈ 7.854 × 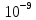 м². м².Тогда 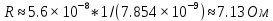 (сопротивление нити). (сопротивление нити).Теперь, используя найденное сопротивление и мощность, рассчитаем ток, который должен идти по нити: 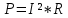 , отсюда I = , отсюда I = 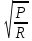 ≈ ≈ 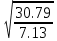 ≈ √4.242 ≈ 2.07 А. ≈ √4.242 ≈ 2.07 А.Таким образом, ток, который должен идти по вольфрамовой нити, чтобы поддерживать ее температуру на 300 К выше температуры трубки, составляет примерно 2.07 А. |
