Тестирование автокорреляции. T1,2T. Поэтому выводы об их независимости осуществляются на основе оценок
 Скачать 132.11 Kb. Скачать 132.11 Kb.
|
|
Введение Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Применение традиционных методов корреляционно-регрессионного анализа для изучения причинно-следственных зависимостей переменных, представленных в форме временных рядов, может привести к ряду серьезных проблем, возникающих как на этапе построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой временных рядов как источника данных в эконометрическом моделировании. Предполагается, что в общем случае каждый уровень временного ряда содержит три основные компоненты: тенденцию (Т), циклические или сезонные колебания (S) и случайную компоненту (E). Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким, что в данном случае есть результат того, что х и у зависят от времени, или содержат тенденцию. Для того чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков за текущий и предыдущие моменты времени, которая получила название «автокорреляция в остатках». В силу неизвестности значений параметров уравнения регрессии неизвестными будут также и истинные значения отклонений εt, t=1,2…T. Поэтому выводы об их независимости осуществляются на основе оценок εt, t=1,2…T, полученные из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции. Тестирование автокорреляции. Графический метод. Существует несколько вариантов графического определения автокорреляции. Один из них, указывающий отклонения εt с моментами t их получении (их порядковыми номерами i), приведен на рис. 1.1. Это так называемые последовательно-временные графики. В этом случае по оси абсцисс обычно откладывают либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат- отклонения εt. 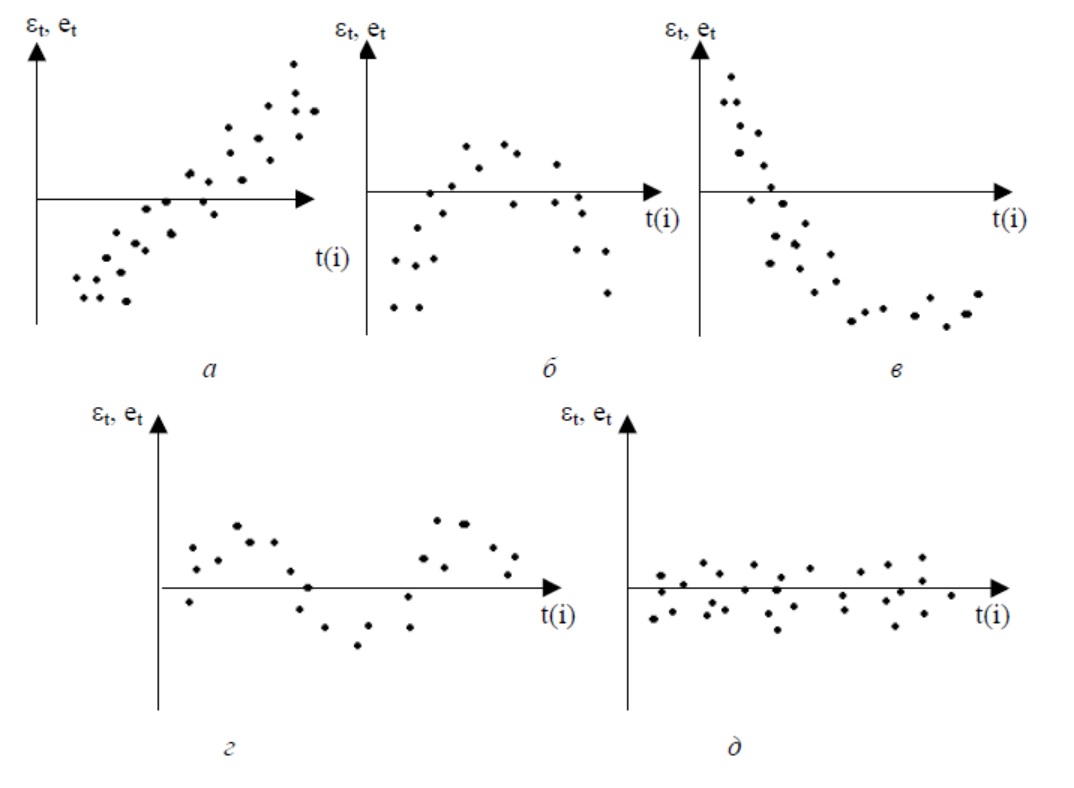 Рис.1.1. Естественно предположить, что на рис 1.1. а-г имеются определенные связи между отклонениями, т.е. автокорреляция имеет место. Отсутствие зависимости на рис. д скорее всего свидетельствует об отсутствии автокорреляции. Например, на рис. 1.1.б отклонения вначале в основном отрицательные, затем положительные, потом снова отрицательные. Это свидетельствует о наличии между отклонениями определенной зависимости. 1.2. Метод рядов. Этот метод достаточно прост: последовательно определяются знаки отклонений et, t=1,2…T. Например, (-----)(+++++++)(---)(++++)(-), т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 наблюдениях. Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда. Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция. Для небольшого числа наблюдений (n1 < 20, n2 < 20) разработаны специальные таблицы критических значений количества рядов при n наблюдениях. В таблице на пересечении строки n1 и столбца n2 определяются нижнее k1 и верхнее k2 значения при уровне значимости а = 0,05: • при k1 < k < k2 автокорреляция остатков отсутствует; • при k < k1 наблюдается положительная автокорреляция остатков; • при k2 < k наблюдается отрицательная автокорреляция остатков. При достаточно большом количестве наблюдений n применяются специальные формулы, которые позволяют ответить на вопрос наличия или отсутствия автокорреляции. 1.3 Тест Дарбина—Уотсона. Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью d-критерия Дарбина-Уотсона. Этот тест считается достаточно универсальным и широко применяется в эконометрических исследованиях вследствие своей простоты, хотя и не обладает существенной эффективностью (достоверностью). Тест Дарбина-Уотсона обычно используется для установления факта наличия автокорреляционной зависимости первого порядка в ряду ошибки, то есть между соседними её значениями. Автокорреляционные зависимости второго и последующих порядков этот тест не обнаруживает. Расчётное значение d-критерия определяется по формуле: 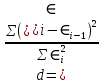 (1.3.1) (1.3.1)Расчетное значение критерия сравнивается с нижним (dн) и верхним (dв) критическими значениями статистики Дарбина-Уотсона. При этом возможны следующие случаи: dв< d < 4–dв, то гипотеза об отсутствии автокорреляции не отвергается (принимается); dн< d 0 < d < dн, то принимается альтернативная гипотеза о положительной автокорреляции; 4–dн< d < 4, то принимается альтернативная гипотеза об отрицательной автокорреляции. Изобразим результат Дарбина—Уотсона графически: 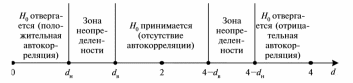 Рис.1.1 Недостатками критерия Дарбина—Уотсона является наличие области неопределенности критерия, а также то, что критические значения d-статистики определены для объемов выборки не менее 15. Тем не менее тест Дарбина—Уотсона является наиболее употребляемым. Тест Дарбина-Уотсона можно применять только в случае выполнения следующих условий: в регрессионном уравнении присутствует свободный член; регрессоры являются нестохастическими; в регрессионном уравнении нет лаговых значений зависимой переменной. 1.4 Тест серий (Бреуша—Годфри). Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении et = ρet−1 + vt, t = 1, …, n, (1.4.1) (где et — остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент ρ окажется значимо отличающимся от нуля. Заметим, что уравнение (1.4.1) является авторегрессионным уравнением первого порядка. Практическое применение теста заключается в оценивании методом наименьших квадратов регрессии (1.4.1) (временной ряд et–1 представляет ряд et со сдвигом по времени на единицу: компьютерные регрессионные пакеты имеют команду, которая формирует по данному временному ряду et ряд et–1). Преимущество теста Бреуша—Годфри по сравнению с тестом Дарбина—Уотсона заключается в первую очередь в том, что он проверяется с помощью статистического критерия между тем как тест Дарбина—Уотсона содержит зону неопределенности для значений статистики d. Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не только остатки с лагом 1, но и с лагом 2, 3 и т д., что позволяет выявить корреляцию не только между соседними, но и между более отдаленными наблюдениями. В большинстве современных компьютерных пакетов (например, в «Eсonometric Views») применение теста серий осуществляется специальной командой, и нет необходимости оценивать регрессию непосредственно. Заключение Таким образом, автокорреляция – это статистическая взаимосвязь между последовательностями величин одного ряда, взятыми со сдвигом, например, для случайного процесса — со сдвигом по времени. В силу ряда причин в регрессионных моделях может иметь место корреляционная зависимость между соседними случайными отклонениями. Это нарушает одну из фундаментальных предпосылок МНК. Вследствие этого оценки, полученные на основе МНК, перестают быть эффективными. Это делает ненадежными выводы по значимости коэффициентов регрессии и по качеству самого уравнения. Поэтому достаточно важным является умение определить наличие автокорреляции и устранить это нежелательное явление. Существует несколько методов определения автокорреляции, среди которых были выделены графический, метод рядов, критерий Дарбина-Уотсона, Бреуша-Годфри. При установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Если после ряда возможных усовершенствований регрессии автокорреляция по-прежнему имеет место, то, возможно, это связано с внутренними свойствами ряда отклонений. Список использованных источников: Эконометрика: учебник для студентов вузов / Н.Ш. Кремер, Б.А. Путко; под ред. Н.Ш. Кремера. — 3-е изд., перераб. И доп. — М.: ЮНИТИ-ДАНА, 2010. — 328 с. — (Серия «Золотой фонд российских учебников»). 174с Эконометрика: учебник / под ред. И. И. Елисеевой. М.: Финансы и статистика, 2002. 144с |
