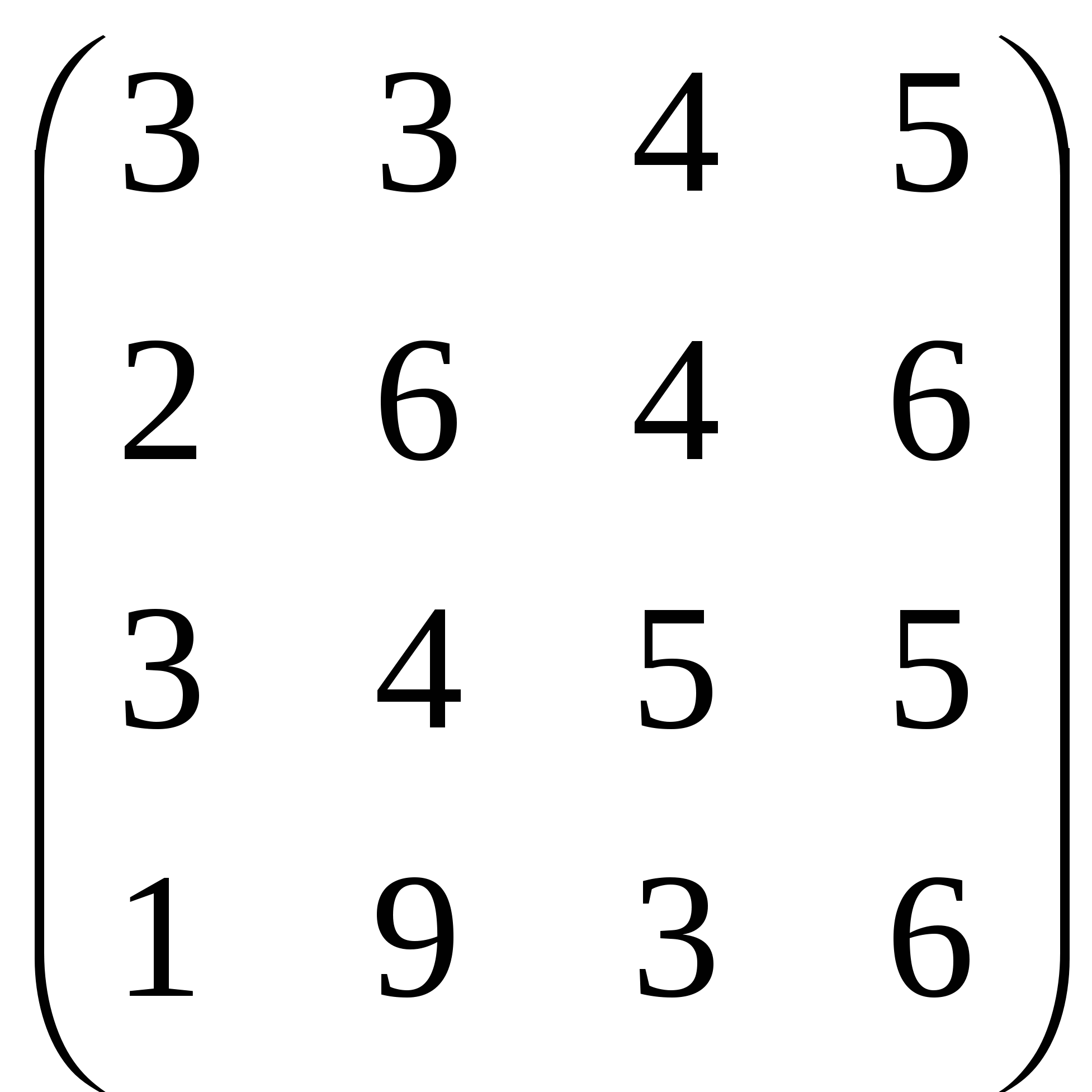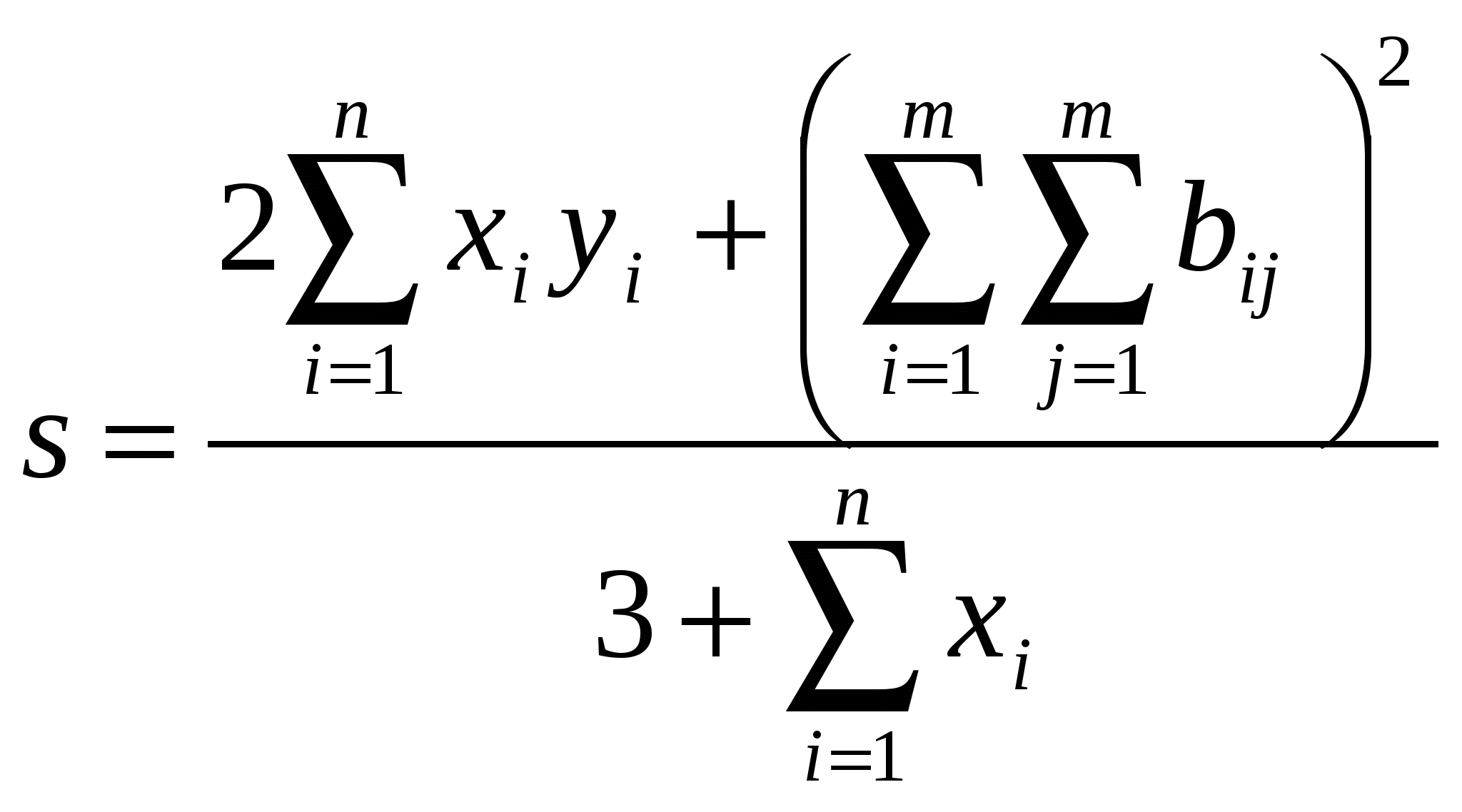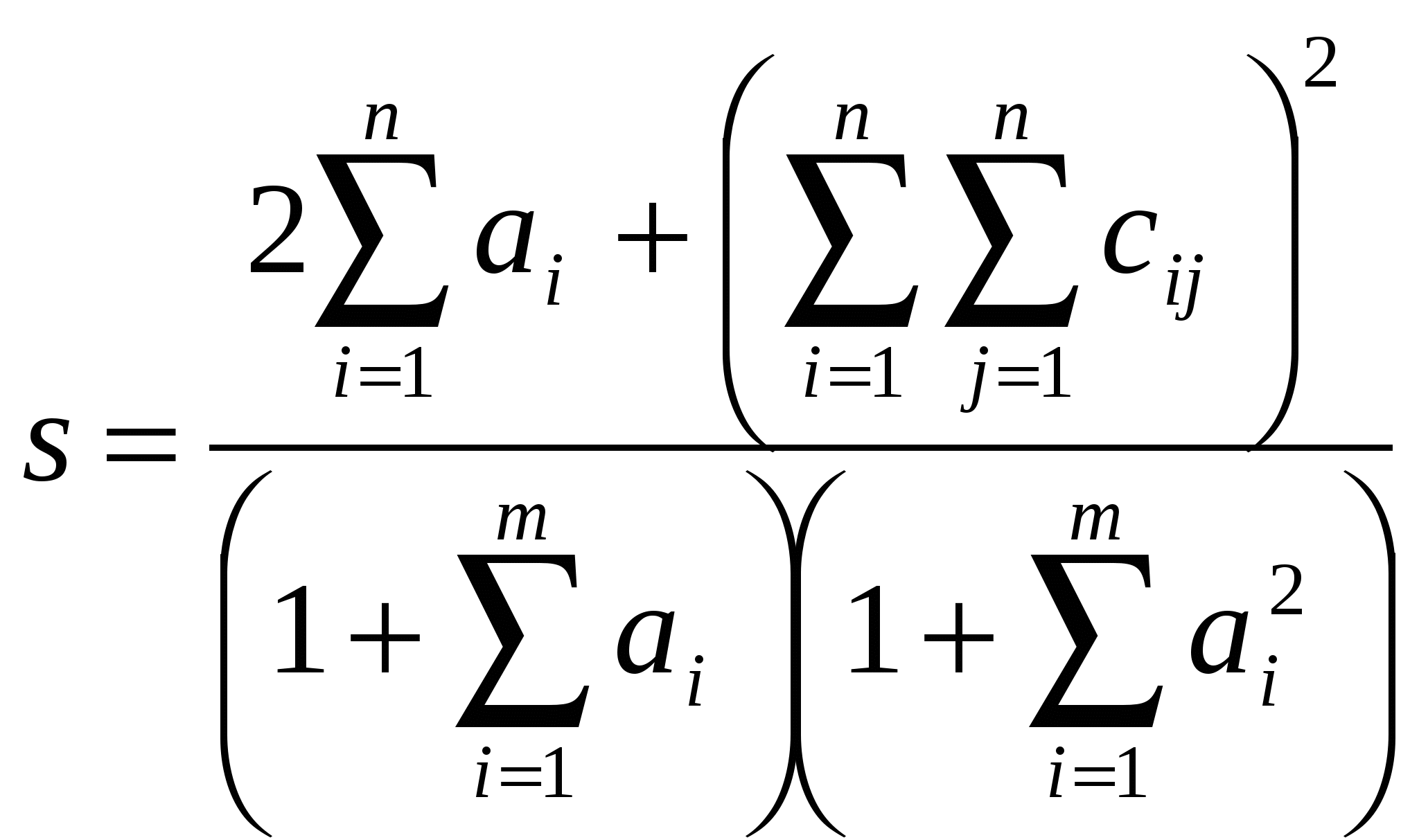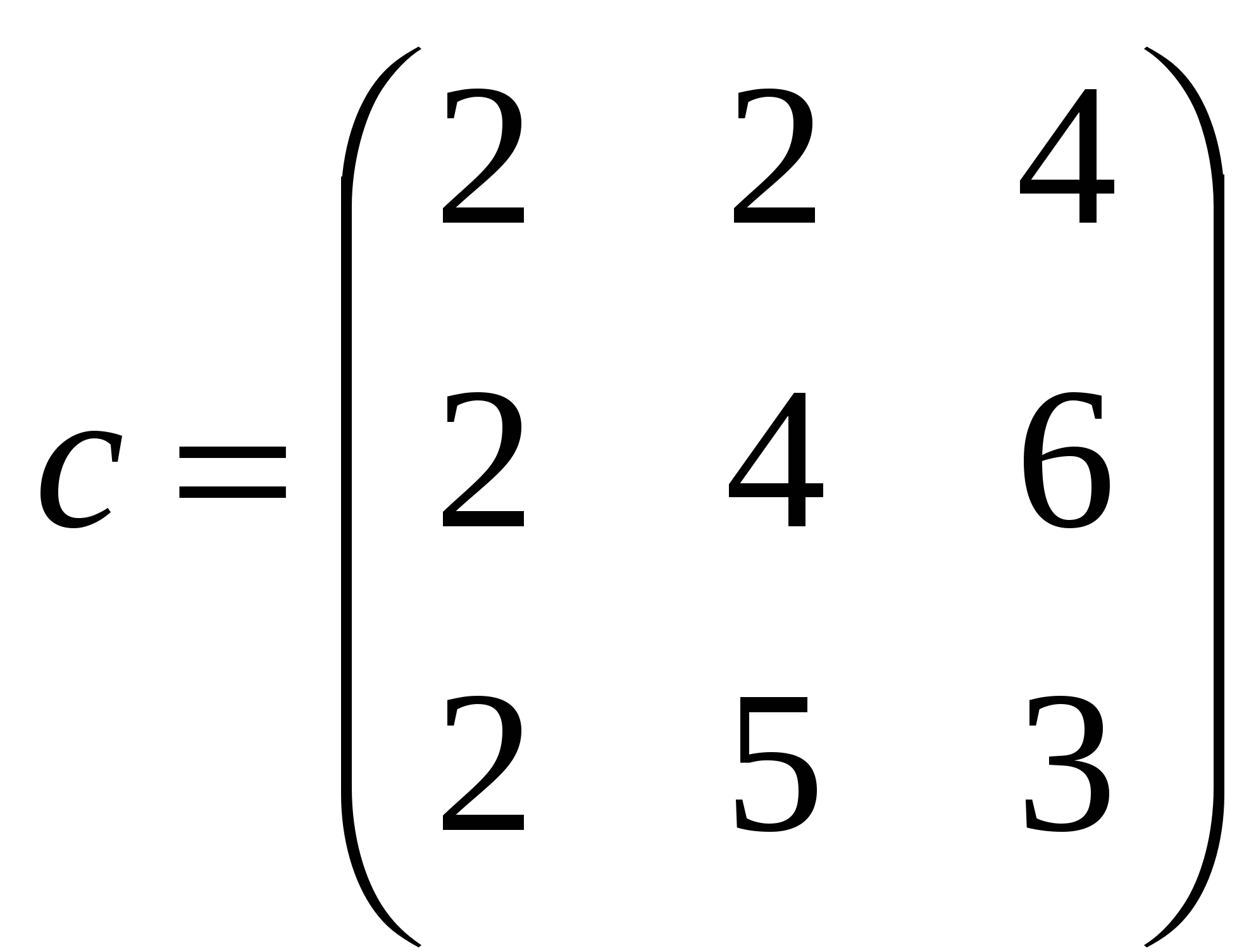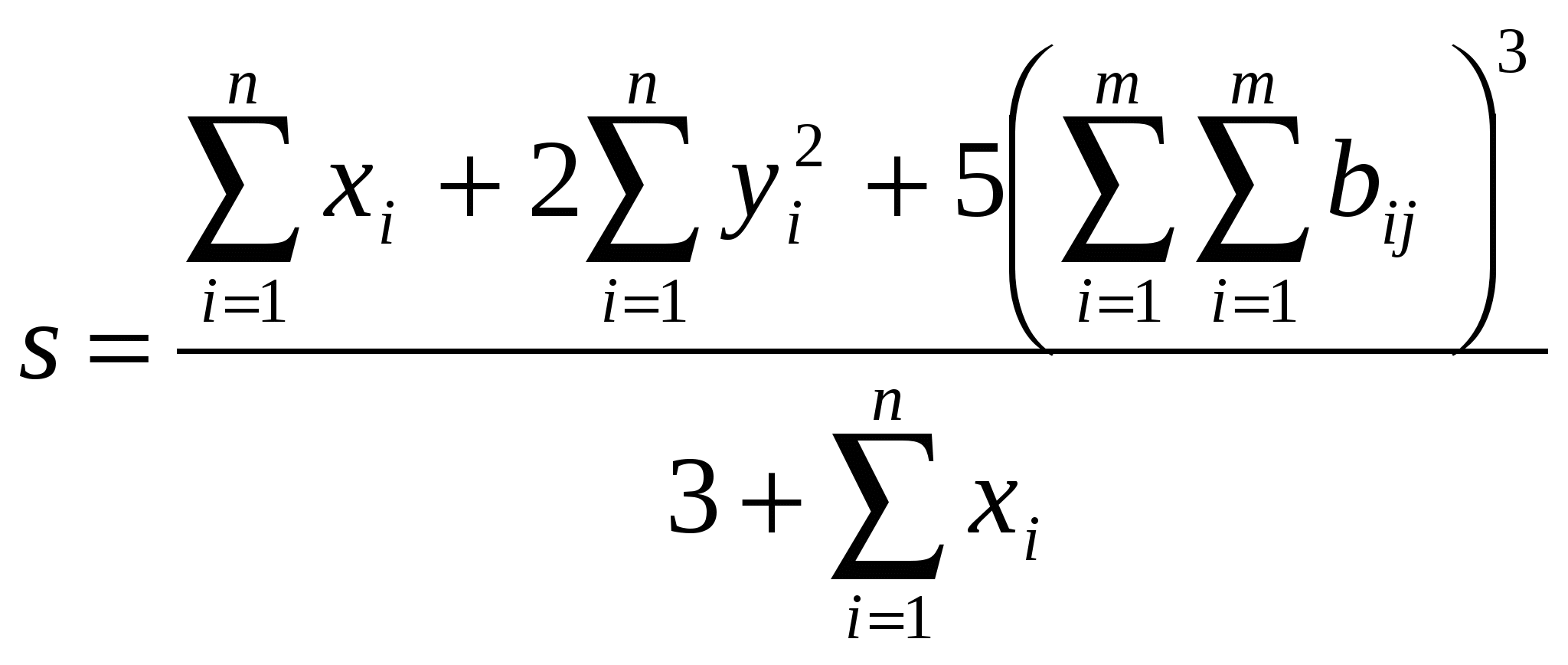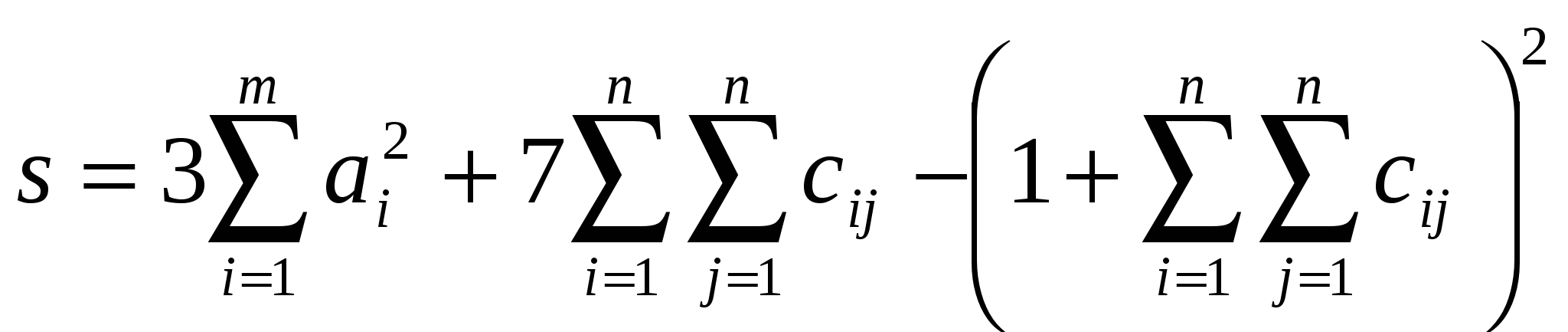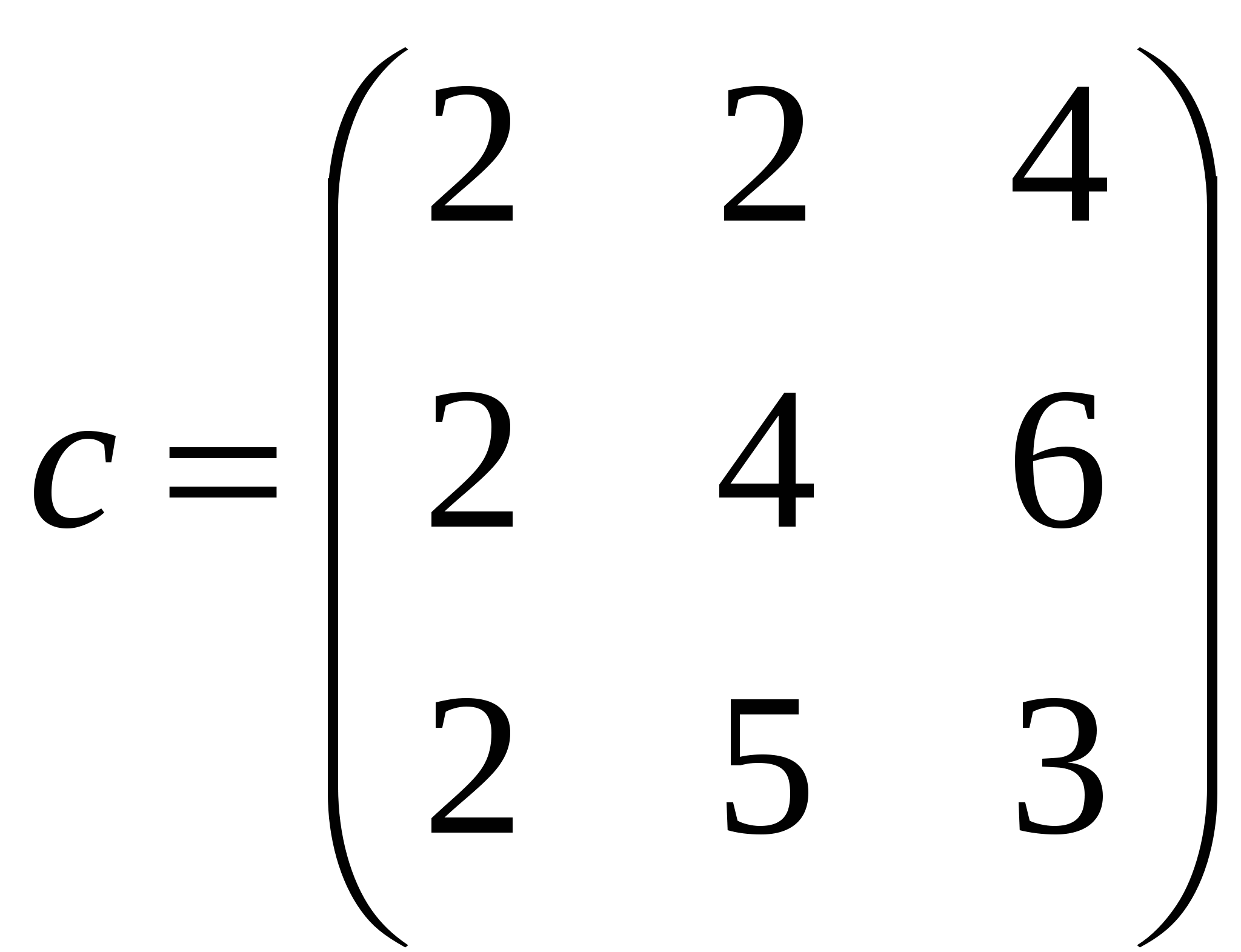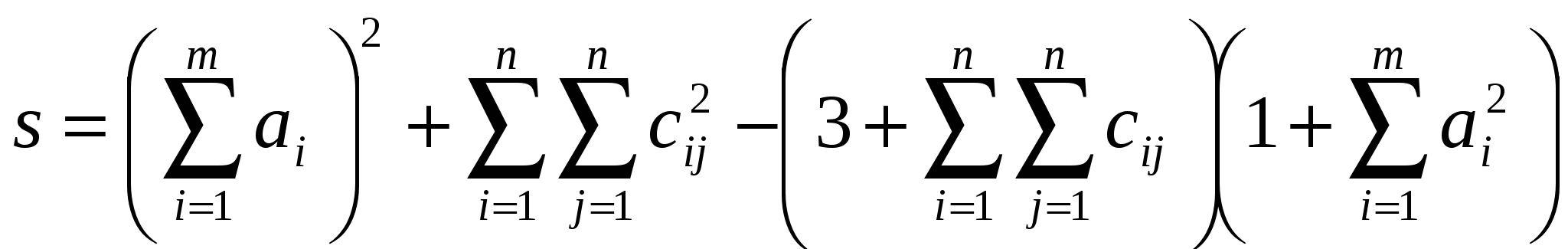Лабораторная работа11. Табличный процессор Excel. Массивы. Вычисление сложных выражений. Метод Крамера
 Скачать 233 Kb. Скачать 233 Kb.
|
|
(()Лабораторная работа № 11 Тема: «Табличный процессор Excel. Массивы. Вычисление сложных выражений. Метод Крамера»Цель работы: сформировать умение вычислять сложные выражения, решать систему линейных уравнений с помощью метода Крамера. Основные понятия: Функция ТРАНСП ( )преобразует вертикальный диапазон ячеек в горизонтальный, и наоборот. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и так далее. Упражнение 1. В качестве применения использования формулы массива приведем расчет цен группы товаров с учетом НДС (налог на добавленную стоимость). 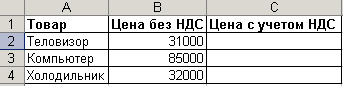 В диапазоне В2:В4 даны цены группы товаров без учета НДС. Необходимо найти цену каждого товара с учетом НДС (который будем полагать равным 25%). Таким образом, необходимо умножить массив элементов В2:В4 на 125%. Результат надо разместить в ячейках диапазона С2:С4. Упражнение__2._Вычисление_функции,_зависящей_от_элементов_массива.'>Упражнение 2. Вычисление функции, зависящей от элементов массива. Пусть в диапазоне А6:В7 имеется некоторый массив данных (введите свои значения). Требуется найти массив, элементы которого равны значениям функции Упражнение 3. Вычислить транспонированную матрицы AT к матрице А
Упражнение 4. Вычисление сложных выражений. 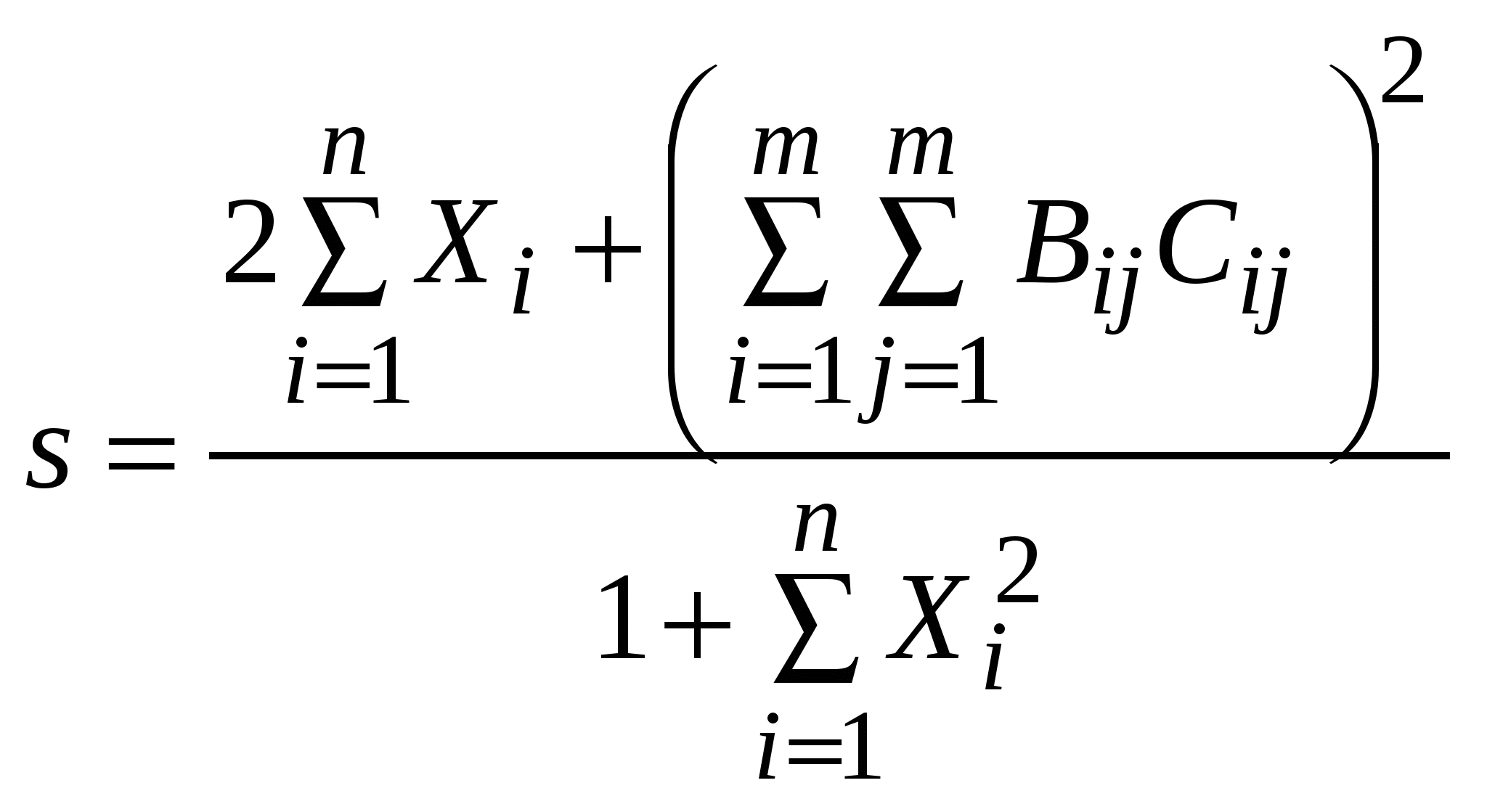 где 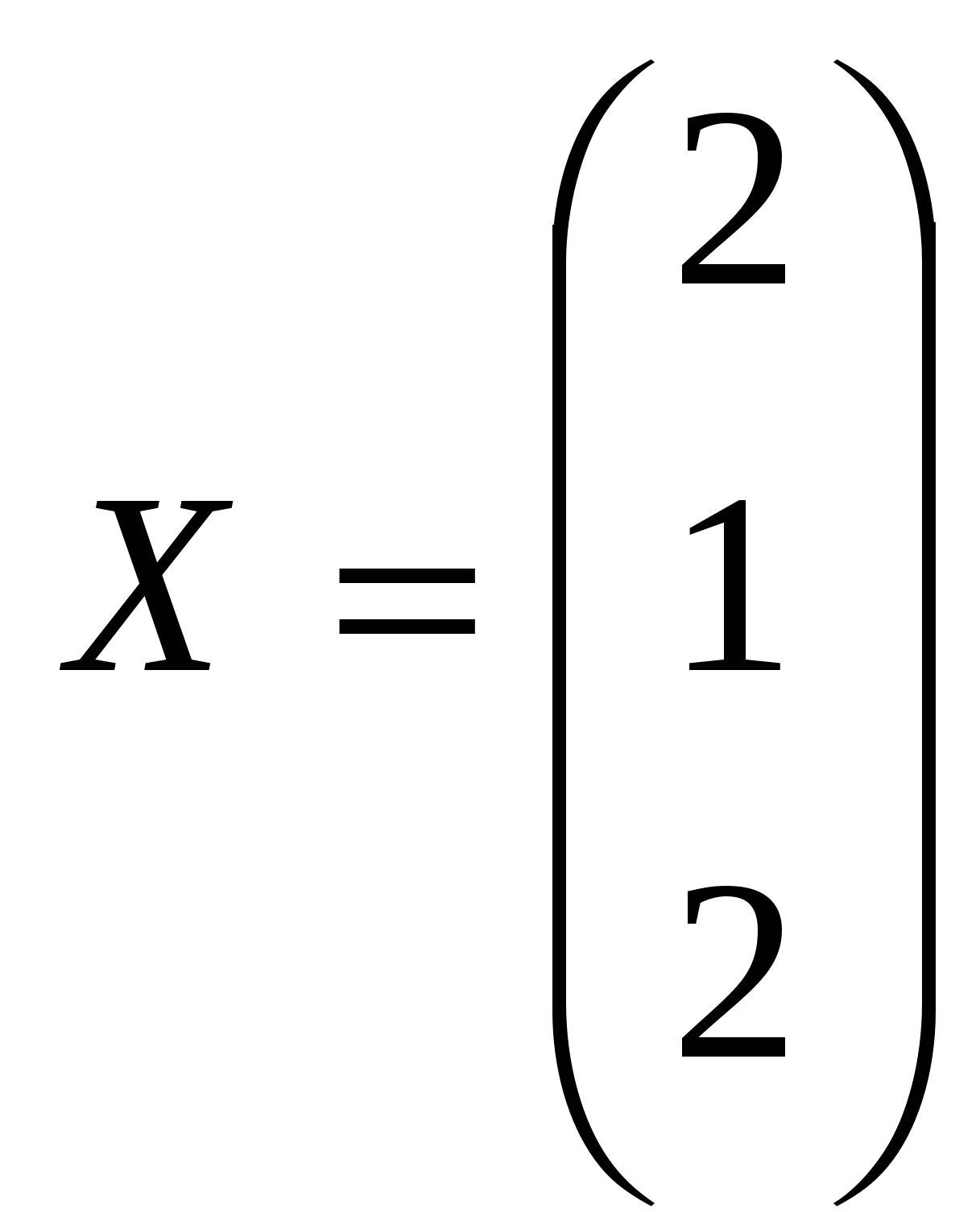 , , , ,
Упражнение 5. Решение системы линейных уравнений Методом Крамера Дана линейная система По методу Крамера Например, нужно решить систему линейных уравнений с 3 неизвестными, с коэффициентами 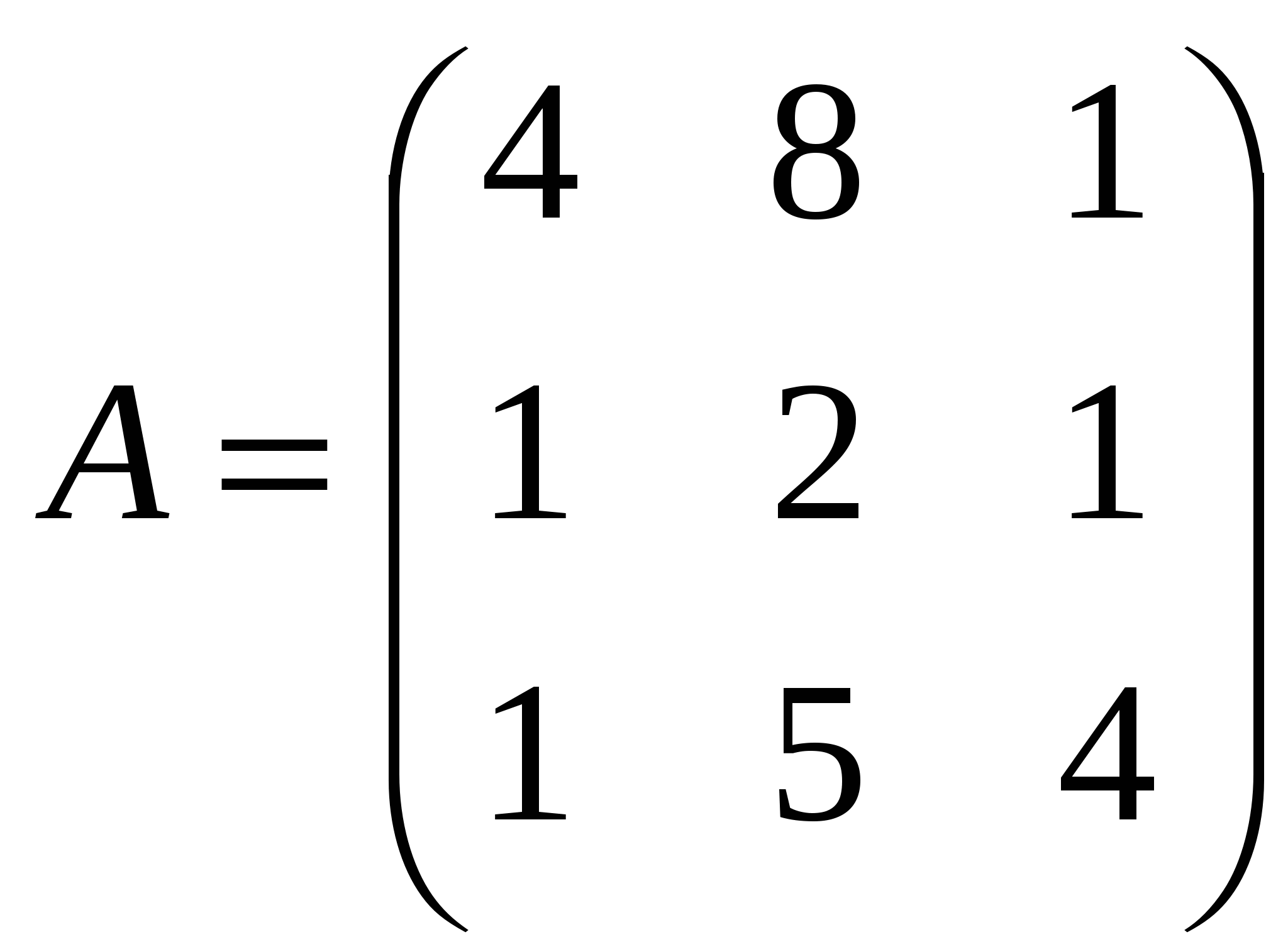 и с правой частью и с правой частью 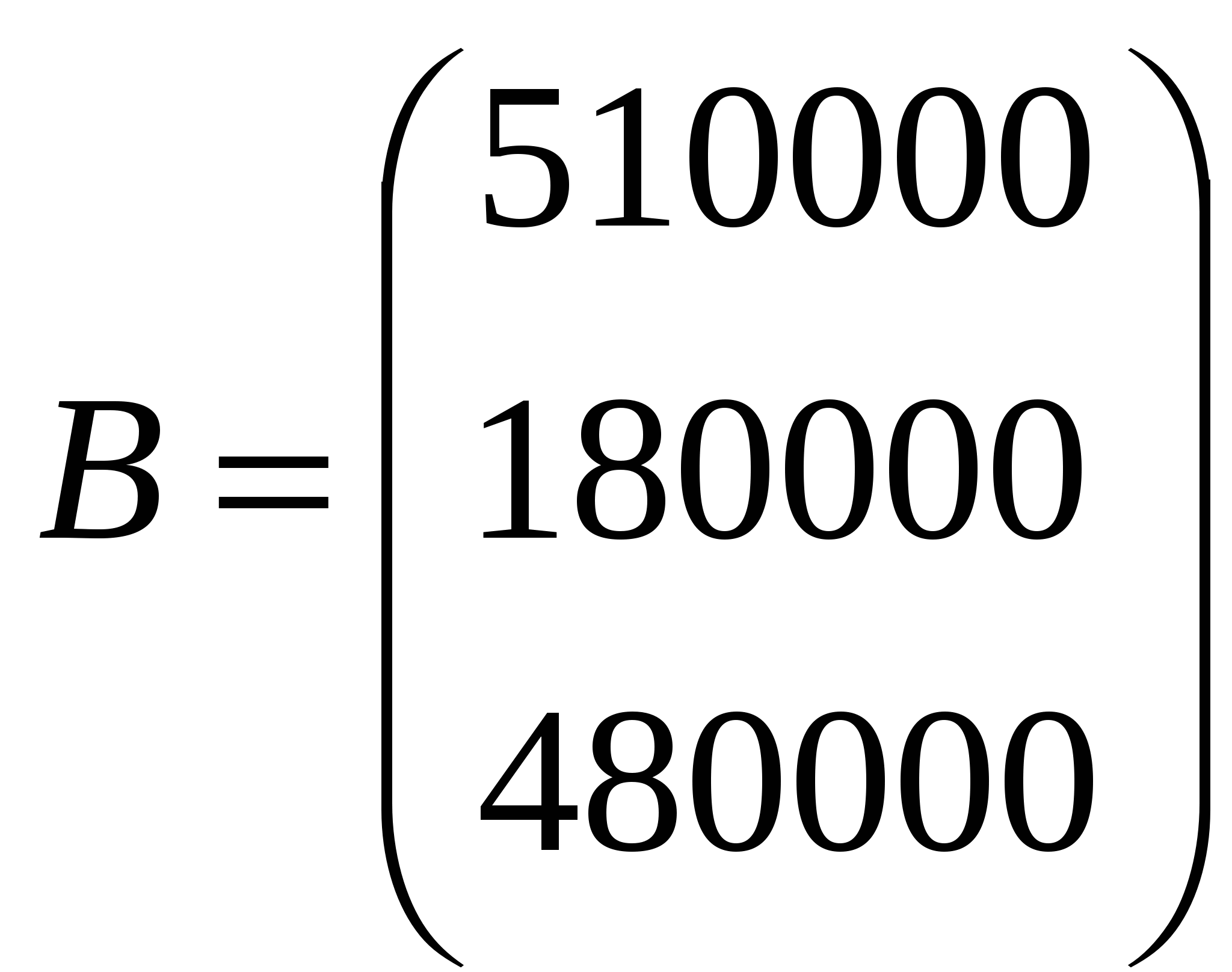 . .
Рис. 1
Задания для самостоятельной работы: 1. Решить системы линейных уравнений а) Методом Крамера 2. Вычислите б) квадратичную форму Таблица 1.
3. Найдите значение сложных выражений Таблица 2.
Контрольные вопросы:
|

 ля решения этой задачи нам потребуется функция рабочего листа
ля решения этой задачи нам потребуется функция рабочего листа