вав. Тактическое планирование модельных экспериментов Цель работы

• Название: Тактическое планирование модельных экспериментов Цель работы
• Дата: 04.03.2023
• Размер: 344.76 Kb.
• Имя файла: lp-takticheskoe-planirovanie-modelnyih-eksp_Wtwpgnw.docx
• Тип: Документы; #967486

Тактическое планирование модельных экспериментов

1. Цель работы

Изучение методов:

1. 
   скользящего среднего для определения стационарного режима,
   
2. 
   повышения эффективности использования ресурсов эксперимента.
   

2. Теоретические сведения

В зависимости от наличия в имитационной модели естественным образом опре­деляемой точки завершения все модели можно подразделять на завершаю­щиеся и на не завершающиеся.

Временная продолжительность имитации процессов в завершающихся моде­лях обусловлена временем протекания реального процесса до достижения им своего логического конца. Таковым может быть, например, конец рабочего дня на моде­лируемом предприятии, окончание исследуемого временного промежутка (ска­жем, периода пиковой загрузки отделения банка), завершение техноло­гичес­кого цикла на производственном участке. Соответственно, время моделирования в таких моделях однозначно определяется внешними условиями.

В не завершающихся моделях четко заданный момент времени окончания процесса отсутствует. К таковым можно отнести производственные процессы на предприятиях с непрерывным циклом, работу операторов “горячей линии”, логи­сти­ческие процессы. Время моделирования в таких моделях должно определяться исследователем.

В большинстве случаев значения выходных параметров завершающихся моде­лей характеризуют переходный (неустановившийся) режим. Это означает, что величина выходного параметра находится в процессе постоянного изменения.

Для не завершающихся моделей более типичным является случай, когда имитируемый процесс достигает стационарного (установившегося) режима. Это не означает, что значения выходных параметров вообще не меняются, в стацио­нар­ном режиме эти изменения подчиняются некоторому распределению, характер­ному для этого режима.

Например, нормальное функционирование какой-либо единицы оборудова­ния поточной линии на непрерывном производстве может нарушаться случаю­щимися остановками ввиду поломок, нарушений подачи энергопитания и т.п. Одна­ко если проводить наблюдение за показателями производительности работы линии в течение длительного промежутка времени, средние значения этих показателей будут оставаться постоянными.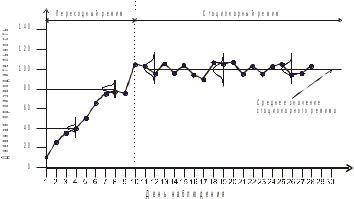



Можно заметить, начиная примерно с десятого дня наблюдения, дневная про­изв­одительность колеблется в небольшом диапазоне вокруг некоторого среднего значения, представляющего собой значение среднего установившегося режима.

Однако начальное состояние процесса, как видно из рисунка, не совпадает с его состоянием в установившемся режиме, поскольку в реальной системе произ­вод­ственная линия находится в стадии наполнения объектами переработки. Поэ­то­му первая фаза представляет собой фазу начального переходного режима.

В случаях, если процесс достигает установившегося состояния, то от его на­ча­льного состояния состо­я­ние в этом режиме не зависит.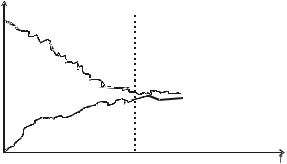



Несмотря на разные начальные условия, две реализации одного о того же процесса имеют тенденцию к схожему поведению примерно правее пунк­ти­р­ной линии, проведенной перпендикулярно оси времени. Область левее этой ли­нии представляет собой переходный режим, область правее – установившийся.

Для не завершающихся моделей основной интерес представляют исследо­ва­ние и оптимизация показателей эффективности по критерию средних значений у­ста­новившегося режима. Поэтому данные, собранные в течение имита­ции началь­ной фазы процесса, нужно рассматривать как искажающие реальную кар­тину и учитывать их в итоговой обработке не следует. Для этого можно прибегнуть к одно­му из двух приемов:

– определение “периода разогрева” модели для исключения его из рассмотрения (прием известен также как метод отсечения);

– установка адекватного начального состояния имитационных прогонов.

3. Содержание работы

Изучение приемов планирования экспериментов для не завершающихся моде­лей проводится на основе модели одноканальной СМО с пуас­со­нов­с­ким входным потоком и экспоненциальным временем обслуживания.

1. 
   Запустите MS Excel и подготовьте рабочий лист (“Разогрев-1”) для занесения выходных параметров эксперимента и результатов их обработки.
   

Область для регистрации результатов прогона и их обработки должна иметь следующий вид:

				Тср(т)	5,000
	N	Тср(1)	Тср(2)	Тср(3)	Тср(4)	Тср(5)	Тср(*)	ΔТср
	1	…….	…….	…….	…….	…….	…….	…….
	2	…….	…….	…….	…….	…….	…….	…….

В верхней строке листа нужно записать То.ср.т. – среднее время ожидания в очере­ди, посчитанное по формуле Хинчина-Полачека.

В столбцы таблицы Т_ср(1) – Т_ср(5) должны записываться результаты за­ме­­ров Т_ср, выполненные средствами, встроенными в программную мо­дель (см. далее).

В столбец Т_о.ср(*) записывается значение, усредненное по пяти запускам про­г­раммной модели.

В столбец ΔТ_о.ср записывается модуль разности экспериментального сред­него и теоретического значений |Т_о.ср(*) – Т _о.ср(т)|.

2. 
   Для проведения эксперимента внимательно изучите исходный текст модуля (см. список При­ло­же­ние A) и соберите проект С++ (см. При­ло­же­ние B).
   
3. 
   Для данных своего варианта выполните пять запусков и внес­ите результаты в журнал (подготовленный лист Excel-книги).
   

Для времени моделирования следует выбирать значение равное примерно (средний интервал прихода заявок) × 500000; число точек замера Т_о.ср зада­ет­­ся равным 50.

4. 
   Запишите нужные выражения для расчета величин в ячейки столбцов Т_о.ср(*) и ΔТ_о.ср.
   

Постройте графики зависимости этих величин от номера замера (иначе говоря, от времени моделирования Т_мод).

Проанализируйте полученные данные и сделайте выводы.

5. 
   Повторите эксперимент, взяв для изучения время пребывания заявок в систе­ме (Т_с.), предварительно подготовив для него отдельный лист “Разогрев-2”: в верхней строке за­пи­шите рассчитанное значение среднего времени нахож­де­ния в системе Т_с.ср.т., таблицу со струк­турой, аналогичной структуре п.1, и внеся нужные изме­не­ния в исходный текст программной модели.
   

Проанализируйте полученные данные и сделайте выводы.

6. 
   В Excel–книге подготовьте рабочий лист “Отсечение”) для занесения вы­ход­ных параметров эксперимента и результатов их обработки.
   
7. 
   Для проведения эксперимента внимательно изучите исходный текст модуля (см. список Error: Reference source not found) и соберите проект С++ (см. Error: Reference source not found).
   
8. 
   Для данных своего варианта (см. работу Error: Reference source not found) и с учетом результатов, по­лу­чен­ных в итоге оценивания времени “разогрева” модели, выполните пять за­пу­с­ков и внес­ите результаты в журнал (лист “Отсечение” Excel-книги).
   

Для времени моделирования следует выбирать значение равное примерно (средний интервал прихода заявок) × 500000 + (время “разогрева”).

Найдите среднее значение и проведите сравнительный анализ.

4. Отчет по работе

Отчет по работе должен включать:

1. 
   Таблицы с выходными данными экспериментов по оцениванию длитель­но­сти переход­ного периода, результатами их обработки и графиками (пп.1–4 и пп.5, листы “Разогрев-1” и “Разогрев-2”).
   

Примерный вид таблицы (фрагмент листа “Разогрев-1”)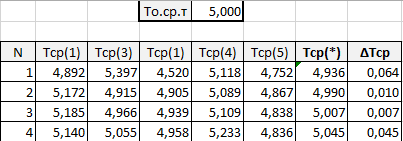



графика Т_о.ср.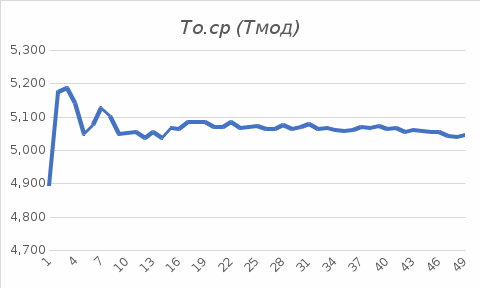



и графика ΔТ_о.ср.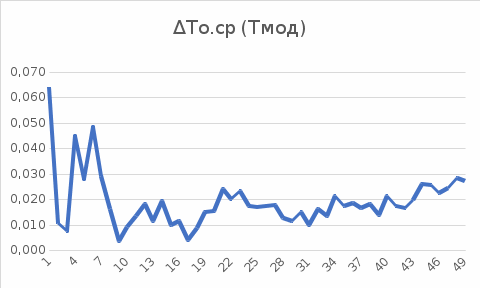

2. 
   Итоги экспериментов с моделью с использованием метода отсечения и выводы (лист “Отсечение”).
   

5. Контрольные вопросы

1. 
   Какими бывают модели по признаку завершаемости моделируемых процессов?
   
2. 
   Какие показатели представляют интерес для завершающихся моделей?
   
3. 
   Какие показатели представляют интерес для не завершающихся моделей?
   
4. 
   Какие различают фазы в процессе моделирования? С какой целью?
   
5. 
   На каких показателях процесса и результата моделирования может отразиться удачно (неудачно) спланированный модельный эксперимент?
   
6. 
   Какие приемами можно пользоваться для организации модельных экспериментов не завершающихся моделей?
   
7. 
   Что такое метод отсечения?
   

6. Варианты исходных данных

См. варианты работы Создание и изучение аналитической и программной (Pilgrim) моделей одноканальной СМО.

7. Задания для самостоятельного решения

1)  Определите тип имитационной модели для изучения работы:

–сервисного центра с целью оценить его среднюю производительность;

–металлургического завода с целью нахождения нужных режимов работы нового оборудования;

–крупного универсама с целью определить наиболее подходящее число касс в часы пиковой загрузки;

–пользователей корпоративной информационной сети с целью определения требований к параметрам оборудования.

2)  Для представленных графиков временной зависимости значения выходного показателя имитационного прогона определите тип модели (завершающаяся или не завершающаяся) и характер процесса (переходный, установившийся, циклический):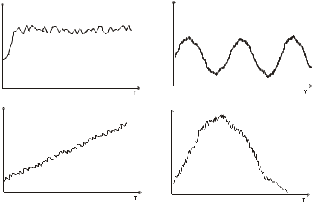



3) Для последовательности представленных в таблице значений выходного параметра в трех реализациях модельного эксперимента, относящихся к последовательным часам наблюдения, найдите момент вхождения процесса в стационарный режим.

№	1	2	3
1	0,0	97,2	139,2
2	0,0	123,2	132,4
3	27,2	128,8	122,0
4	138,8	93,2	127,2
5	130,0	145,6	152,4
6	120,8	140,0	151,6
7	104,0	135,6	148,0
8	99,2	142,0	153,6
9	67,6	159,2	144,4
10	83,2	156,0	138,8
11	68,0	136,8	122,8
12	130,0	120,4	135,2
13	128,4	90,8	159,2
14	127,2	154,0	166,8
15	139,6	142,8	134,8
16	142,8	116,4	121,2
17	134,8	105,2	90,4
18	126,4	100,0	105,6
19	130,8	107,2	78,0
20	146,0	83,2	112,8
21	132,0	118,4	158,4
22	144,8	130,4	147,2
23	140,0	143,6	142,8
24	127,2	151,2	138,4
25	87,2	136,8	117,6