Расчет последовательного колебательного контура. Техническая эксплуатация транспортного радиооборудования
 Скачать 422.67 Kb. Скачать 422.67 Kb.
|
 Федеральное агентство морского и речного транспорта Федеральное агентство морского и речного транспортаФедеральное государственное бюджетное образовательное учреждение высшего образования «Государственный университет морского и речного флота имени адмирала С.О. Макарова» Институт МОРСКАЯ АКАДЕМИЯ Кафедра «Основ судовой электроэнергетики» КУРСОВАЯ РАБОТА по дисциплине «Электротехника и электроника» на тему «Расчет последовательного колебательного контура» Специальность 25.05.03 «Техническая эксплуатация транспортного радиооборудования» Выполнила: Неверова М. В. Группа Р-241 Проверил: преподаватель Росляков Р. О. Задание на выполнение курсовой работы Исследуемая цепь изображена на рис.1. Для цепи заданы все параметры: активное сопротивление R, индуктивность катушки L, ёмкость конденсатора C, амплитудное значение Um и начальная фаза ψu приложенного синусоидального напряжения, угловая частота сети ω. Варианты заданий приводится в табл. 1-2. Требуется: 1. Рассчитать индуктивное сопротивление XL, емкостное сопротивление XС, реактивное сопротивление X, полное сопротивление Z, комплексное сопротивление Z,угол сдвига фаз φ между напряжением u и током i на входе схемы. 2. Используя заданные амплитудное значение Um и начальную фазу ψu приложенного синусоидального напряжения, а также угловую частоту сети ω, написать выражение для мгновенного значения напряжения u. Определить действующее значение напряжения U и комплексное действующее значение напряжения U. 3. Рассчитать комплексное действующее значение тока I, действующее значение тока I, амплитудное значение тока Im. Записать выражение длямгновенного значения тока i. 4. Рассчитать комплексные действующие значения падений напряжений на активном сопротивлении UR, на индуктивности UL, на ёмкости UС. Определить комплексное действующее значение реактивного напряжения Uр. 5. Построить на комплексной плоскости вектор тока и векторную диаграмму напряжений. 6. Определить мощности цепи: активную Р, индуктивную QL, ёмкостную QС, реактивную Q, полную S и комплексную S. 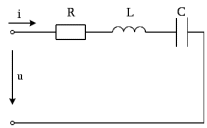 Рис. 1. Схема последовательного колебательного контура Исходные данные для расчета - вариант № 19 из таблицы 2.
Решение Рассчитаем индуктивное сопротивление XL, емкостное сопротивление XС, реактивное сопротивление X, полное сопротивление Z, комплексное сопротивление Z,угол сдвига фаз φ между напряжением u и током i на входе схемы. Индуктивное сопротивление XL= ω∙L= 103∙12∙10-3 = 12 Ом. Ёмкостное сопротивление 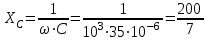 Ом. Ом.Реактивное сопротивление X=XL - XС = 12 – 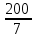 = - = -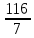 Ом. Ом.Полное сопротивление 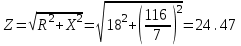 Ом. Ом.Комплексное сопротивление 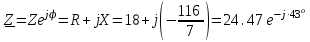 Ом. Ом.Угол сдвига фаз φ между напряжением u и током i 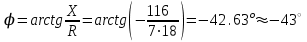 . .Используя заданные амплитудное значение Um и начальную фазу ψu приложенного синусоидального напряжения, а также угловую частоту сети ω, написать выражение для мгновенного значения напряжения u. Определить действующее значение напряжения U и комплексное действующее значение напряжения U. Мгновенное значение напряжения 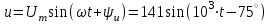 . .Действующее значение напряжения 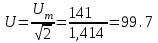 В. В.Комплексное действующее значение напряжения 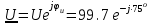 В. В.Рассчитать комплексное действующее значение тока I, действующее значение тока I, амплитудное значение тока Im. Записать выражение длямгновенного значения тока i. Комплексное действующее значение тока 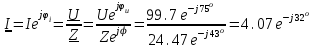 А. А.Действующее значение тока I = 4.07 А. Амплитудное значение тока Im = 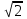 I = I =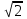 * 4.07 = 5.76 А. * 4.07 = 5.76 А.Мгновенное значение тока 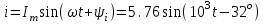 А. А.Рассчитать комплексные действующие значения падений напряжений на активном сопротивлении UR, на индуктивности UL, на ёмкости UС. Определить комплексное действующее значение реактивного напряжения Uр. Комплексное действующее значение падения напряжения на активном сопротивлении 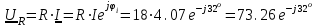 В. В.Комплексное действующее значение падения напряжения на индуктивности 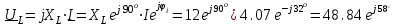 В. В.Комплексное действующее значение падения напряжения на ёмкости 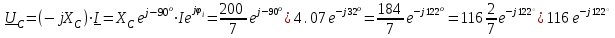 В. В.Комплексное действующее значение реактивного напряжения 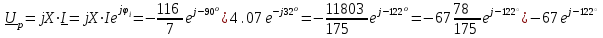 В. В.Построить на комплексной плоскости вектор тока и векторную диаграмму напряжений. Выбираем масштабы напряжения и тока. На комплексной плоскости в масштабе тока из начала координат под углом ψi = -32о к оси действительных чисел откладываем вектор комплексного действующего значения тока I. Комплексное действующее значение напряжения на активном сопротивлении UR совпадает по фазе с комплексным действующим значением тока I. Т.е. вектора I и UR совпадают по направлению. В масштабе напряжения из начала координат откладываем вектор UR. Перпендикулярно вектору тока в сторону опережения (против часовой стрелки) в масштабе напряжения из начала координат откладываем вектор комплексного действующего значения напряжения на индуктивности UL. Аналогичным образом перпендикулярно вектору тока, но в сторону отставания (по часовой стрелке) в масштабе напряжения из начала координат откладываем вектор комплексного действующего значения напряжения на ёмкости UС. Вектора UL и UС находятся в противофазе. На комплексной плоскости эти вектора лежат на одной прямой, но направлены в противоположные стороны, поскольку вектор UL опережает по фазе вектор тока I на 90о, а вектор UС отстает по фазе от вектора тока I на 90о. Вектор Uр представляет собой сумму векторов UL и UС. В нашем примере вектор Uр совпадает по направлению с вектором UС. Сумма векторов UR и Uр определяет вектор комплексного действующего значения входного напряжения U. Вектор U располагается под углом ψu = -75о по отношению к оси действительных чисел. Между векторами U и I угол φ = -43о. Отсчет угла φ ведется от вектора тока I к вектору напряжения U. В нашем примере угол φ направлен по часовой стрелке, т.е. отрицательный. (Вектор тока I в примере опережает по фазе вектор напряжения U). При отрицательном угле φ цепь является активно-емкостной нагрузкой. 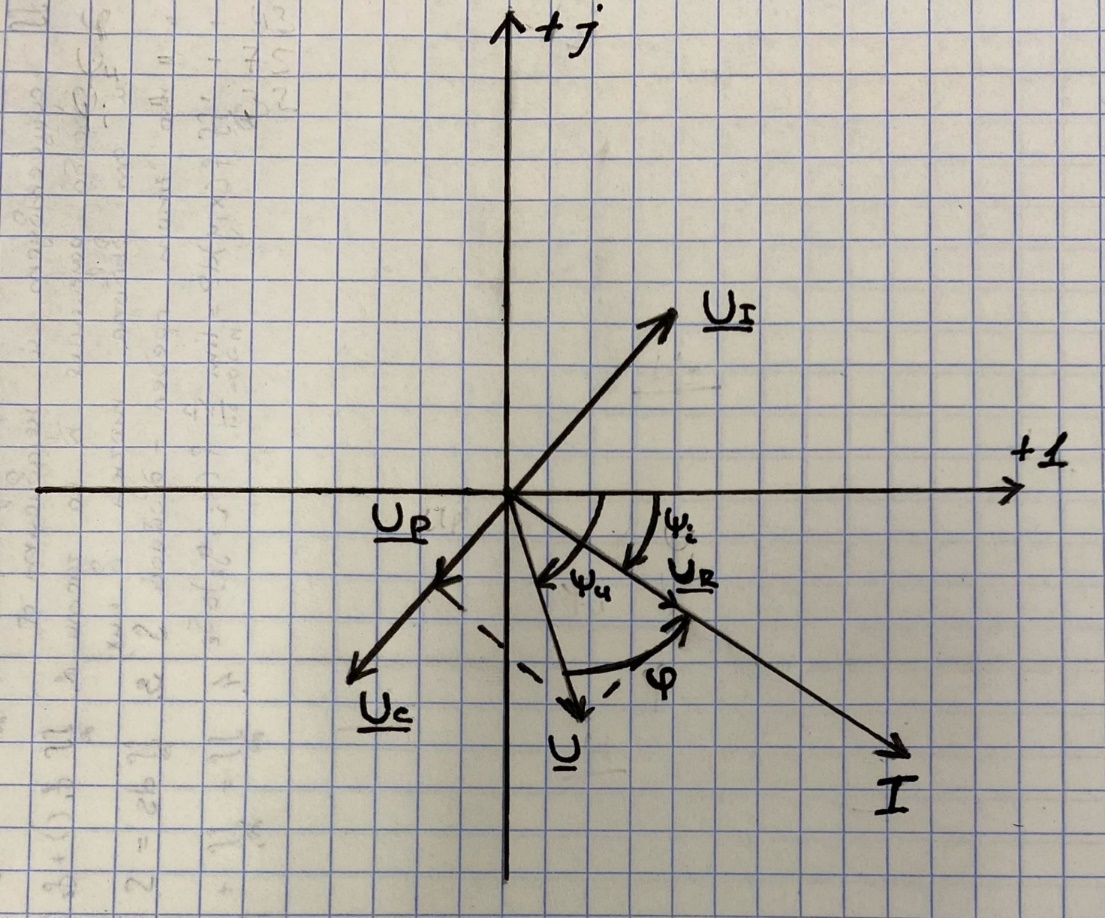 Рис. 2. Векторная диаграмма напряжений Определить мощности цепи: активную Р, индуктивную QL, ёмкостную QС, реактивную Q, полную S и комплексную S. Активная мощность цепи 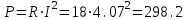 Вт. Вт.Индуктивная мощность цепи 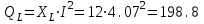 вар. вар.Ёмкостная мощность цепи 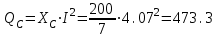 вар. вар.Реактивная мощность цепи 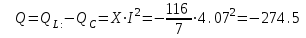 вар. вар.Полная мощность цепи 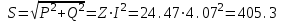 ВА. ВА.Комплексная мощность цепи 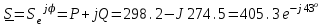 ВА. ВА.Санкт-Петербург 2022 |
