Лекция. Система теплозащиты.. Тема 8 Проектирование системы теплозащиты са
 Скачать 461 Kb. Скачать 461 Kb.
|
|
Приложение 1. Расчёт теплового режима конструкции теплозащиты. В качестве наружного тепловой защиты СА используются разлагающиеся теплозащитные материалы. Градиенты температуры в теплозащите вдоль образующей наружной поверхности, как правило, существенно больше, чем по нормали к поверхности. В связи с этим расчет прогрева ТЗП можно проводить в одномерной постановке. Поле температур в пакете теплозащитных материалов может быть рассчитано путем интегрирования следующей системы дифференциальных уравнений: 1. Уравнение теплопроводности с учетом конвективного переноса тепла продуктами разложения наружного материала: где с, r, l - теплоемкость (Дж/(кг К)), плотность (кг/м3) и теплопроводность (Вт/(м ))материала пакета; mg, hg - массовый расход и теплосодержание продуктов разложения; t - время, с. 2. Уравнение сохранения массы разлагающихся компонентов в наружном материале пакета: где k=r/r0 - коксовое число разлагающегося материала; r0 - исходная плотность материала, кг/м3; r - текущая (на данный момент времени) плотность материала, кг/м3; C=(k-kk)/(1-kk) – концентрация разлагающихся компонентов; kk - конечное (минимальное) коксовое число. Скорость разложения наружного материала пакета определяется законом Аррениуса где kR - константа скорости реакции разложения; n - порядок реакции; E - энергия активации, Дж/моль; R=8.31 Дж/(моль К) - универсальная газовая постоянная. Уравнения записаны в неподвижной системе координат с началом на внутренней поверхности пакета. При наличии уноса материала записывается соотношение для определения скорости разрушения наружного материала пакета. Эти зависимости определяются, как правило, экспериментально, и их форма существенно зависит от типа рассматриваемого материала. Для решения приведенной системы уравнений необходимо задать начальные и граничные условия. В качестве начальных условий задается распределение температуры в пакете к моменту начала расчета (как правило, Т=Т0=const). Граничные условия задаются следующие: а) На наружной поверхности пакета х=хw: где e - интегральная полусферическая степень черноты поверхности; s=5.67×10-8 Вт/(м2 К4) – постоянная Стефана-Больцмана; qk, qr - конвективный и лучистый тепловые потоки к наружной поверхности, Вт/м2; qвд – уменьшение конвективного теплового потока за счет вдува в пограничный слой газообразных продуктов разрушения материала, Вт/м2. Конвективный тепловой поток с учетом вдува qw=qk-qвд можно выразить по формуле Ньютона как qw = (a/ср)w (J0-Jw). Тогда qw/qk=(a/ср)w/(a/ср)=y. Показано, что в случае ламинарного пограничного слоя y=1-0,67(Mв/Мg)0,25fw при fw<1.5 и y=1-(Mв/Мg)0,25exp(0.23-(0.3fw+0.45)) при fw>1.5, а в случае турбулентного y=1-0,19(Mв/Мg)nfw, где fw=mg/(a/ср) – формфактор; Мв, Мg – молекулярные массы воздуха и продуктов разложения ТЗМ, кг/моль; mg – массовый расход продуктов разложения, кг/м2. Методы расчета конвективного теплового потока для конусов и сферического затупления кратко изложены выше. Лучистый тепловой поток при скоростях движения, меньших первой космической, пренебрежимо мал по сравнению с конвективным. б) На внутренней поверхности пакета (х=0) задается условие теплоизоляции: При необходимости могут быть рассмотрены и условия, аналогичные приведенным выше для наружной поверхности. Для решения системы уравнений (1), (2) применен метод конечных разностей, основанный на замене производных на их приближенные значения, выраженные через разности значений функции в отдельных дискретных точках – узлах сетки. Дифференциальные уравнения в результате таких преобразований заменяются эквивалентными соотношениями в конечных разностях. Конечно-разностный аналог уравнения теплопроводности (1) записывается по смешанной схеме, неявной для членов, описывающих теплопроводность (эти члены берутся на j–ом шаге по времени при расчете j–го шага), и явной для членов описывающих фильтрацию газа (mg, hg берутся на предыдущем (j-1)-ом временном шаге). Для краткости запишем конечно-разностную аппроксимацию уравнения теплопроводности для случая постоянных шагов по времени Dt и пространству Dх (в случае переменных шагов уравнения не сложнее, но более громоздкие): где i, j – номера узлов пространственной и временной сеток соответственно. Уравнение (2) с учетом (3.3) записывается в форме и интегрируется по методу парабол от зоны начала разложения х* до наружной поверхности пакета хw. Следует отметить, что для неразлагающихся материалов уравнение (2) не используется, а в уравнении (1) и его конечно-разностном аналоге (6) исключаются члены с массовым расходом. Уравнение (6) решается методом прогонки. Суть метода состоит в следующем: Перепишем уравнение (6) в виде aiTi-1+biTi+giTi+1=-di (8), где ai = Предположим, что имеет место рекуррентное соотношение Ti=AiTi+1+Bi (9). Тогда вторые прогоночные коэффициенты определяются из соотношений: Ai=-gi/(aiAi-1+bi), Bi=-(di –ai Bi-1)/(aiAi-1+bi) (10). Значения нулевых прогоночных коэффициентов определяются из аппроксимации граничного условия на внутренней поверхности: A0 = 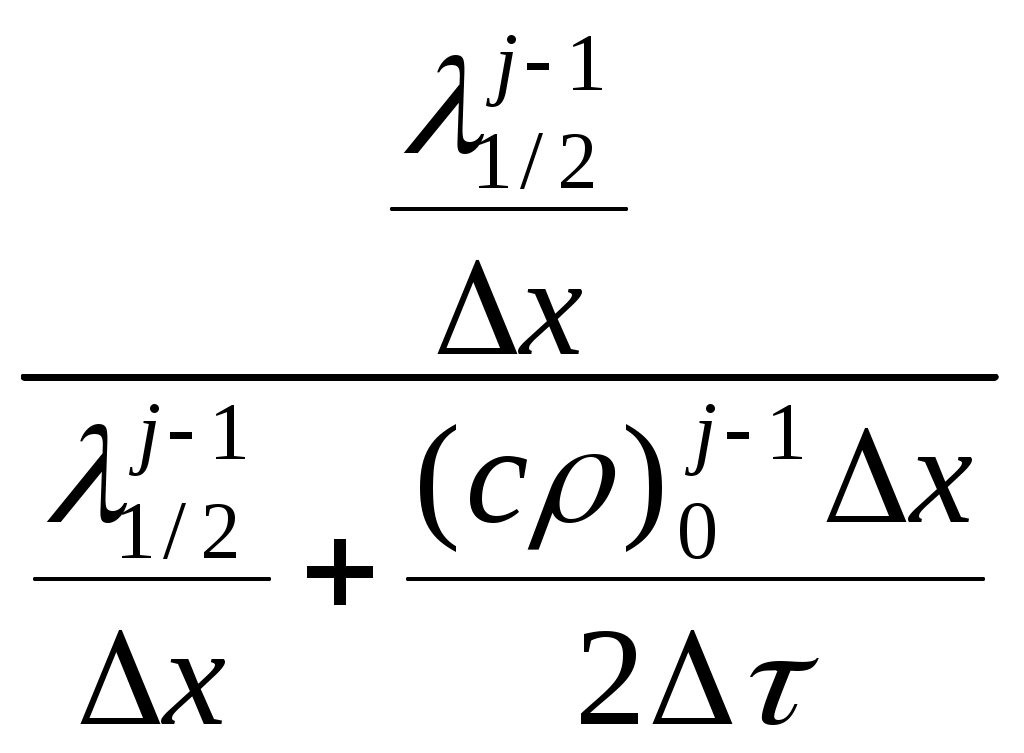 , B0 = , B0 = 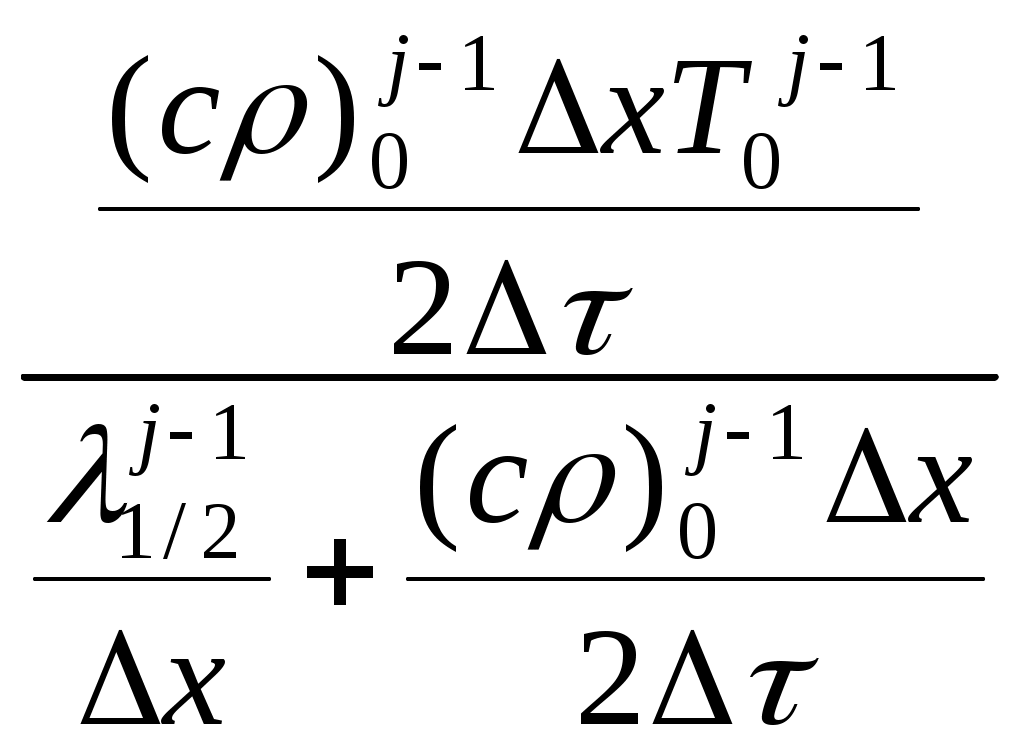 (11) (11)Теперь, зная в любой момент времени j (начиная с начального j=0) распределение температур в пакете, определяем коэффициенты А0, В0 и первые прогоночные коэффициенты для всех слоев сетки. Из граничного условия на внешней поверхности определяем температуру наружной поверхности в момент времени j+1, а затем обратной прогонкой, начиная с наружной поверхности, по (9) полное поле температур на момент j+1. Таким образом, получаем распределение температур в ТЗП и конструкции корпуса для всего времени полета. Приложение 2. Определение толщин слоёв теплозащитного покрытия При определении необходимых толщин теплозащитных материалов (ТЗМ), как правило, требуется получить пакет минимальной общей массы, обеспечивающий температуру корпуса, не превышающую заданной величины в течение заданного времени. Часто приходится учитывать дополнительные факторы, влияющие на состав ТЗП и толщины составляющих его материалов: конструктивные или технологические ограничения на общую толщину ТЗП или отдельных ТЗМ; прочностные характеристики ТЗМ, способ их соединения в пакет и связанная с этим прочность всего ТЗП; способ крепления ТЗП к корпусу; ограничение на максимально допустимую температуру ТЗМ, связанное с изменением его физических свойств (потерей прочности материалом или разложением клея, например), и тому подобное. Не следует забывать и о стоимости ТЗМ, их технологичности и вредности для окружающей среды (это касается в основном разлагающихся материалов). В общем случае выбор оптимальной теплозащиты представляет собой многопараметрическую задачу минимизации с ограничениями, осложненную, как правило, неполнотой информации. Остается открытым и вопрос о единственности получаемого решения. Обычной практикой является нахождение минимальных толщин уже выбранных ТЗМ при наличии ограничений по максимальной температуре корпуса и самих материалов пакета. Литература. Хейз У.Д., Пробстин Р.Ф. Теория гиперзвуковых течений. М. ИЛ. 1962 г. Проблемы движения головной части ракет дальнего действия. Сборник статей. М. ИЛ. 1959 г. Гребер Г., Эрк С., Григуль У. Основы учения о теплообмене. М. ИЛ. 1958 г. Кошкин В.К. и др. Основы теплопередачи в авиационной и ракетно-космической технике. М. 1975 г. Проблемы полета с большими скоростями. Сборник статей. М. ИЛ. 1960 г. Огнеупоры для космоса. Справочник. М. Металлургия. 1967 г. Лох У. Динамика и термодинамика спуска в атмосфере планет. М. МИР. 1968 г. Сейферт Г. Космическая техника. Сборник статей. М. Наука.1964 г. Дракин И.И.. Аэродинамический и лучистый нагрев в полете. М. Оборонгиз. 1961 г. Фэй Дж. А., Ридделл Ф.Р. Теоретический анализ теплообмена в лобовой точке, омываемой диссоциированным воздухом. Сборник статей. Проблемы движения головной части ракет дальнего действия. М. ИЛ. 1959 г. Полежаев Ю.В., Юревич Ф.Б.. Тепловая защита. М. Энергия. 1976 г. Чиркин В.С. Теплофизические свойства материалов. М. ФМ. 1959 г. Панкратов Б.М. Основы теплового проектирования транспортных космических систем. М. МАШ. 1988 г. Тримпи Р.Л., Грант Ф.С., Коэн Н.Б.. Проблемы аэродинамики и нагревания при входе перспективных летательных аппаратов в атмосферу. Сборник Газовая динамика космических аппаратов. М. МИР. 1965 г. Аллен Х. Дж. Газодинамические проблемы космических летательных аппаратов. Сборник Газовая динамика космических аппаратов. М. МИР. 1965 г. Чепмен Д.Р. Приближенный аналитический метод исследования входа тел в атмосферы планет. М. ИЛ. 1962 г. Эккерт Э.Р., Дрейк Р.М. Теория тепло - и массообмена. Л. Госэнергоиздат. 1961 г. Проблемы полета с большими скоростями. Сборник статей под ред. Кудрявцева Е.В. М. ИЛ. 1960 г. Лох У. Динамика и термодинамика спуска в атмосфере планет. М. МИР. 1966 г. Босворт Р.Ч.Л. Процессы теплового переноса. М. Изд. ТТЛ.1957 г. Романенко П.Н.. Гидродинамика и теплообмен в пограничном слое. Справочник. М. Энергия. 1974 г. Михеев М.А., Михеева И.М. Основы теплопередачи. М. Энергия. 1973 г. Вопросы для проверки по теме. Анализ работы теплозащитных систем возвращающихся космических аппаратов. Пассивные и активные системы теплозащиты. Использование абляционных материалов. Система охлаждения ответственных элементов конструкции. Радиационная система теплозащиты. Особенность конструктивного выполнения схемы с радиационными экранами. Номенклатура используемых теплозащитных материалов и жаростойких сплавов в современной космической технике. Инженерные методы определения величин тепловых потоков и температур поверхности космических спускаемых аппаратов. Метод Кемпа и Ридделла для оценки теплового режима сферического затупления. Методика расчёт прогрева пакета теплозащитного покрытия СА на участке спуска. Массовые характеристики систем теплозащиты СА класса «Союз». |
