метод Лагранжа. Зад-01-03-ИП. Тема Интерполирование функций
 Скачать 121.63 Kb. Скачать 121.63 Kb.
|
|
Контрольные задания по теме «Тема 1.3. Интерполирование функций» 1.3.1. Общее заданиеПолучить вариант задания и номера задач в нем. Если функция задана аналитически, получить таблицу значений функции в узлах, необходимых для проведения ее интерполяции. Построить по таблично заданной функции интерполяционный многочлен. При необходимости получить таблицу конечных разностей. Получить значение функции в заданной точке без использования ПК. Решить задачу интерполяции с использованием средств заданного математического пакета. Сравнить полученные результаты. 1.3.2. Варианты контрольной работы по теме «Интерполирование функций»Вариант № 1 Построить интерполяционный многочлен Лагранжа для функции, заданной таблично, и вычислить значение функции в точке х=0.18
Определить степень интерполяционного полинома, которым можно заменить функцию, заданную следующей таблицей
Вариант № 2 Построить интерполяционный многочлен Ньютона для функции, заданной таблично, и вычислить значения функции в точках х=0,12 и х=0.29
Определить приближенное значение функции 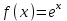 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 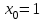 и и 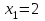 . .Вариант № 3 Построить интерполяционный многочлен Лагранжа для функции, заданной таблично, и вычислить значение функции в точке х=2.25
Определить приближенное значение функции 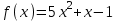 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 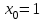 и и 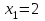 . .Вариант № 4 Построить интерполяционный многочлен Лагранжа для функции, заданной таблично, и вычислить значение функции в точке х=4.5
Определить приближенное значение функции 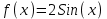 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 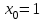 и и 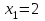 . .Вариант № 5 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, значение функции в точке х=4,2 равно…
Определить приближенное значение функции 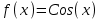 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 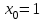 и и 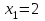 . .Вариант № 6 Построить интерполяционный многочлен Лагранжа L2(х) для функции, заданной таблично, значение функции в точке х=1.36
Определить приближенное значение функции 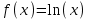 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 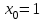 и и 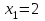 . .Вариант № 7 Вычислить значение функции, заданной таблично, в точке х=6,9 с использованием линейной и квадратичной интерполяции
Определить приближенное значение функции 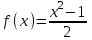 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 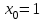 и и 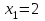 Вариант № 8 Построить интерполяционный многочлена Ньютона Р1(х) для функции, заданной таблично, и найти значение функции в точке х=2,6
Определить приближенное значение функции 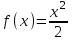 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 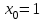 и и 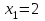 Вариант № 9 При построении линейного интерполяционного многочлена Лагранжа 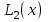 для функции, заданной таблично, значение функции в точке х=2,6 равно… для функции, заданной таблично, значение функции в точке х=2,6 равно…
Определить приближенное значение функции 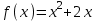 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 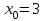 и и 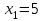 . .Вариант № 10 Для функции, заданной таблично, определить степень интерполяционного многочлена, обеспечивающего наименьшую погрешность
Определить приближенное значение функции 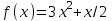 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 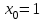 и и 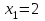 . .Вариант № 11 Построить интерполяционный многочлена Ньютона Р1(х) для функции, заданной таблично, и вычислить значения функции в точках х=1,4 и х=2,8
Определить приближенное значение функции 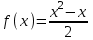 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 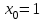 и и 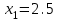 . .Вариант № 12 Построить интерполяционный многочлен 2-й степени для функции, заданной таблично, и вычислить значение функции в точке х=2,5
Определить приближенное значение функции 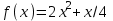 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 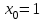 и и 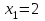 Вариант № 13 Построить интерполяционный многочлен 2-й степени для функции, заданной таблично, и вычислить значение функции в точке х=0,65
Определить приближенное значение функции 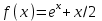 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 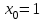 и и 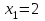 Вариант № 14 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, и вычислить значения функции в точках х=0,44 и х=0,78
Определить степень интерполяционного полинома, которым можно заменить функцию, заданную следующей таблицей
Вариант №15 Построить интерполяционный многочлен 2-й степени для функции, заданной таблично, и вычислить значение функции в точке х=1,15
Определить степень интерполяционного полинома, которым можно заменить функцию, заданную следующей таблицей
Вариант № 16 Построить интерполяционный многочлен Лагранжа 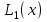 для функции, заданной таблично, и вычислить значение функции в точке х=2,65 для функции, заданной таблично, и вычислить значение функции в точке х=2,65
Определить значение функции 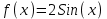 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 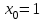 и и 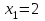 Вариант № 17 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, и вычислить значения функции в точках х=6,1 и х=9,1
Определить приближенное значение функции 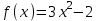 в точке х=2, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=2, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 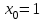 и и 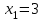 , ,Вариант № 18 Построить интерполяционный многочлен Лагранжа 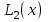 для функции, заданной таблично, и вычислить значение функции в точках х=2,65 и х=3.33 для функции, заданной таблично, и вычислить значение функции в точках х=2,65 и х=3.33
Определить приближенное значение функции 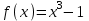 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 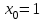 и и 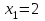 . .Вариант № 19 Построить интерполяционный многочлен Лагранжа 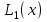 для функции, заданной таблично, и вычислить значение функции в точке для функции, заданной таблично, и вычислить значение функции в точке
Определить приближенное значение функции 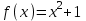 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 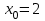 и и 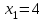 . .Вариант № 20 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, и вычислить значения функции в точках х=0,156
Определить приближенное значение функции 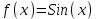 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 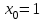 и и 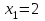 . .Вариант № 21 Построить интерполяционный многочлен Лагранжа 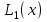 для функции, заданной таблично, и вычислить значение функции в точке х=2,25 для функции, заданной таблично, и вычислить значение функции в точке х=2,25
Определить приближенное значение функции 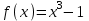 интерполяционным многочленом первой степени, построенным по узлам интерполяционным многочленом первой степени, построенным по узлам 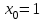 и и 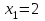 . .Вариант № 22 Получить значение функции, заданной таблично, в точке х=0.21 с использованием первой и второй формул Ньютона
Определить приближенное значение функции 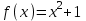 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 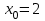 и и 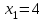 . .Вариант № 23 Построить интерполяционный многочлен Лагранжа 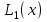 для функции, заданной таблично, и вычислить значение функции в точке х=2,2 для функции, заданной таблично, и вычислить значение функции в точке х=2,2
Определить приближенное значение функции 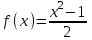 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 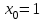 и и 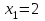 . .Вариант № 24 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, и вычислить значения функции в точках х=3,56
Определить приближенное значение функции 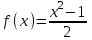 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Ньютона по узлам 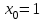 и и 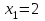 . .Вариант № 25 Построить интерполяционный многочлен Ньютона Р2(х) для функции, заданной таблично, и вычислить значение функции в точке х=0,11
Определить приближенное значение функции 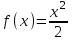 в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам в точке х=1.5, вычисленное с использованием интерполяционного многочлена Лагранжа по узлам 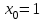 и и 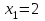 . . 1.3.3. Пример выполнение контрольный заданий по теме«Тема 1.3. Интерполирование функций»КЗ по теме «Тема 1.3. Интерполирование функций» Страница |
