ЛЕКЦИЯ 1 -БН СКН (1). Тема лекции 1

• Название: Тема лекции 1
• Дата: 05.12.2022
• Размер: 0.62 Mb.
• Имя файла: ЛЕКЦИЯ 1 -БН СКН (1).docx
• Тип: Лекции; #829973

Дисциплина: Бортовые и наземные системы и комплексы навигации

Тема лекции №1.

Основные термины, понятия и определения навигации летательных аппаратов. Навигационные системы координат

Навигация в широком смысле слова – это определение параметров поступательного движения объекта. Задачи навигации на летательных аппаратах (ЛА) заключаются в нахождении текущего местоположения, скорости и направления движения, в определении оптимальной траектории и режима полета для перемещения ЛА в заданную точку пространства (цель, аэродром). Также к задаче навигации относят определение ориентации ЛА в пространстве относительно поверхности Земли.

Самолетовождение — это наука о точном, надежном и безопасном вождении воздушных судов из одной точки земной поверхности в другую. Под самолетовождением понимается также комплекс действий экипажа самолета и работников службы движения, направленных на обеспечение безопасности, наибольшей точности выполнения полетов по установленным трассам (маршрутам) и прибытия в пункт назначения в заданное время.

Основными задачами экипажа самолета гражданской авиации при осуществлении самолетовождения являются:

• 
  точное выполнение полета по установленной трассе (маршруту);
  
• 
  определение навигационных элементов, необходимых для выполнения полета по установленному маршруту или поставленной специальной задачи (фотографирование, сбрасывание груза и др.);
  
• 
  обеспечение прибытия самолета к пункту назначения и выполнение посадки на аэродроме в заданное время;
  
• 
  обеспечение безопасности полета.
  

Для решения указанных задач экипаж использует современные технические средства самолетовождения, которые подразделяются по месту расположения, по характеру использования и по принципу действия.

Задачи навигации и самолетовождения при их трактовке в широком и узком смысла и их информационная взаимосвязь показаны на рисунке 1, где используются следующие обозначения:

ЗПВТ – заданная пространственно-временная траектория; ТНБ – точность, надежности и безопасность; ПН – пилотажно-навигационный;



Рисунок 1. Задачи навигации и самолетовождения, их взаимодействие
По месту расположения технические средства навигации/самолетовождения на бортовые) и наземные, а по характеру использования — на автономные и неавтономные.

Автономными называются такие средства, применение которых не требует специального наземного оборудования.

Неавтономными называются средства, которые выдают информацию на основе их взаимодействия с наземными устройствами.

По принципу действия технические средства самолетовождения делятся на четыре группы:

• 
  геотехнические средства, основанные на измерении различных параметров естественных (геофизических) полей Земли. К этой группе относятся магнитные компасы, барометрические высотомеры, указатели воздушной скорости, термометры наружного воздуха, часы, гирополукомпасы, дистанционные гиромагнитные и гироиндукционные компасы, курсовые системы, авиагоризонты, указатели поворота, оптические визиры, навигационные индикаторы, инерциальные системы и др. Большинство из этих средств устанавливается на всех самолетах и используется в любом полете; они применяются также при пользовании другими техническими средствами самолетовождения;
  
• 
  радиотехнические средства, основанные на измерении параметров электромагнитных полей, излучаемых специальными устройствами, находящимися на борту самолета или на земле. К ним относятся: самолетные радиокомпасы и связные радиостанции, радиовысотомеры, самолетные радиолокационные станции, доплеровские измерители угла сноса и путевой скорости, наземные радиопеленгаторы, приводные и радиовещательные станции, радиомаяки, радиомаркеры и наземные радиолокаторы.
  

Самолетное радионавигационное оборудование и наземные радиотехнические устройства образуют системы самолетовождения. По дальности действия последние делятся на системы дальней навигации (свыше 1000 км), ближней навигации до 1000 и системы посадки самолетов.

Радиотехнические средства широко применяются при выполнении полетов на больших высотах, над морем, безориентирной местностью, в сложных метеорологических условиях и ночью, а также при заходе на посадку.

• 
  астрономические средства, основанные на использовании небесных светил. К этой группе средств относятся астрономические компасы, авиационные секстанты и астрономические ориентаторы.
  

Преимуществом астрономических средств является их автономность, помехозащищенность и независимость точности их работы ни от дальности, ни от продолжительности полета. Они могут применяться в любое время суток и в любом месте Земного шара для выдерживания направления полета и определения местонахождения самолета.

Высоты полета

Истинная (или геометрическая) высота - это высота над пролетаемой местностью, т.е. расстояние от ЛА до ближайшей точки земной поверхности. Она служит для контроля полета на малых высотах, а также при взлете и посадке. Измеряется радиовысотомером.

Барометрическая высота (баровысота) - это высота относительно какого-то места, например, аэродрома, измеренная косвенным способом по атмосферному давлению. Баровысоту измеряет система воздушных сигналов (СВС). В зависимости от выбранного уровня отсчета различают две барометрические высоты:

• 
  абсолютную, отсчитываемую от уровня Мирового океана (В РФ – от среднего уровня Балтийского моря);
  
• 
  относительную, отсчитываемую от определенной местности на земной поверхности (чаще всего - от уровня аэродрома взлета или посадки).
  

По абсолютной баровысоте осуществляется эшелонирование воздушных судов, она используется при штурманских расчетах. Относительную баровысоту контролируют при взлете и заходе на посадку.

Геодезическая высота – одна из геодезических координат (наряду с широтой и долготой), определяемая как расстояние по нормали от гладкой поверхности модели земного эллипсоида. Геодезическую высоту определяет спутниковая навигационная система. Геодезическая высота не учитывает существование суши. Используемая модель представляет собой поверхность морей и океанов в спокойном состоянии, мысленно проложенную под материками.

Скорости полета

При полете ЛА принято различать несколько видов скоростей.

Истинная воздушная скорость – это скорость движения ЛА относительно воздушной среды.

Индикаторная скорость – это истинная воздушная скорость, приведенная к нормальной плотности воздуха (ρ=1,225 кг/см3). Если полет проходит при нормальной плотности воздуха, индикаторная скорость совпадает с истинной. Индикаторная скорость определяется по скоростному напору встречного воздуха. Скоростной напор p=ρV²/2 зависит не только от скорости V, но и от плотности воздуха ρ, поэтому определенная таким образом скорость содержит методическую погрешность. Однако аэродинамические силы, действующие на ЛА в полете. пропорциональны скоростному напору, поэтому для поддержания требуемого режима полета важно знать не истинную воздушную, а индикаторную скорость полета.

Приборная скорость – та же индикаторная, она отличается тем, что учитывает методическую и инструментальную погрешности измерения. Истинная скорость функционально связана с приборной, однако ее значение зависит также от давления и температуры воздуха. С подъемом на высоту давление атмосферы понижается, что приводит к росту истинной скорости полета. На высоте 12 000 м истинная скорость превышает приборную вдвое.

П
утевая скорость – это горизонтальная составляющая скорости движения самолета относительно земли. От воздушной скорости она отличается потому, что на движение ЛА влияет ветер. Путевая скорость W равна геометрической сумме горизонтальных составляющих воздушной скорости V и скорости ветра U:

При отсутствии сноса ветром путевая скорость совпадает с воздушной.

Относительная скорость или число Маха (число М) – это отношение истинной воздушной скорости к скорости звука. Начиная с числа М=0,7 ,.. 0,8 в условиях обтекания крыла происходят качественные изменения: появляются скачки уплотнения, вызывающие значительное возрастание сопротивления, изменение устойчивости и управляемости (это явление называется «волновой кризис»). Поэтому на околозвуковых скоростях важно знать не столько скорость полета, сколько число М. На разных высотах волновой кризис наступает при разных скоростях, но при одном и том же числе М. Знание числа М также позволяет повысить эффективность полета, особенно для реактивных самолетов.

Скорость полета является векторной величиной, для определения которой необходимо знать модуль и направление. Направление вектора истинной воздушной скорости в системе координат, связанной с осями ЛА, определяется углами атаки и скольжения.

В целях удобства пилотирования вектор скорости представляют в виде двух составляющих: путевой скорости (горизонтальная составляющая скорости полета ЛА) и вертикальной скорости V_y (вертикальная составляющая).

Направление полета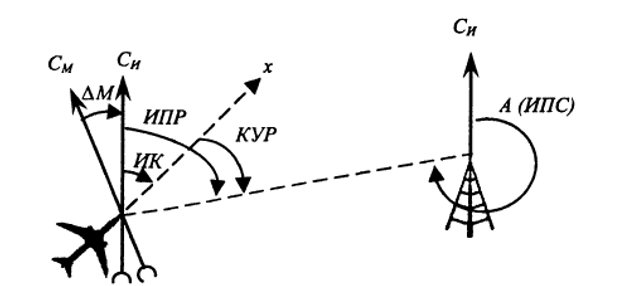

Курсом называется угол между северным направлением меридиана, проходящего через ЛА, и горизонтальной проекцией продольной оси ЛА (рис. 2).
Рисунок 2. Направление на ориентир и на ЛА
Северное направление может указывать на географический полюс С_и, тогда курс называется истинным (ИК), или на магнитный полюс С_м, тогда курс называется магнитным (МК). Истинный и магнитный курс отличаются на величину магнитного склонения ∆М.

Курсовым углом ориентира (например, курсовым углом радиостанции (КУР)) называют угол между горизонтальной проекцией продольной оси ЛА x и направлением на ориентир.

Пеленгом ориентира называется угол между северным направлением меридиана, проходящего через ЛА, и направлением на ориентир. Как и курс, пеленг может быть истинным (ИПР) и магнитным (МПР). Соответственно, ИПР=ИК+КУР, а МПР=МК+КУР.

Азимутом ЛА (пеленгом ЛА) А называют угол в горизонтальной плоскости между северным направлением меридиана, проходящего через ориентир, и направлением на ЛА из точки нахождения ориентира. Различают истинный пеленг ЛА (ИПС) и магнитный (МПС).

Форма Земли и ее геометрические модели

Для решения навигационных задач в околоземном пространстве существенное значение имеет используемое математическое описание формы Земли.

Решение навигационных задач возможно на поверхности некоторых геометрических фигур, имеющих аналитическое описание. Реальная поверхность Земли, ограниченная водной поверхностью и рельефом суши, является весьма сложной и не имеет математического описания.

Первым по точности приближением к форме Земли является геоид. Геоид – это геометрическая фигура, ограниченная так называемой основной уровенной поверхностью Земли, то есть поверхностью, совпадающей с поверхностью мирового океана в состоянии полного покоя водных масс и продолженной под материками (рис. 3).
Рис. 3. Геоид

Основная уровенная поверхность перпендикулярна силе тяжести, представляющей сумму гравитационной и центробежной сил, и аналитического описания не имеет.

Б
олее грубым приближением является эллипсоид вращения, который в данном случае при совпадении малой оси с осью вращения Земли называется земным эллипсоидом (эллипсоидом Клеро) (рис. 4).

Рис. 4. Земной эллипсоид (эллипсоид Клеро)

Земной эллипсоид полностью описывается большой или экваториальной полуосью a и малой полярной полуосью b. Его также характеризует полярное сжатие c, квадрат первого эксцентриситета e², квадрат второго эксцентриситета e’².

Эллипсоид, ориентированный в теле Земли из условия минимума погрешностей аппроксимации основной уровенной поверхности на некоторой её части, называется референц-эллипсоидом. По американским данным 1966 – 1967 гг. параметры земного эллипсоида составляют: a = 6378142 + 6 м, c = 1: 298, 255 + 0,005. В нашей стране ещё в советское время введён референц-эллипсоид Красовского, имеющий a = 6378245,000 км, b = 6356863,019 км, c = 0,0033523299, e² = 0,0066934216, e’² = 0,0067385254.

Решение геометрических задач на поверхности земного эллипсоида (определение расстояний между двумя точками, направлений из одной точки в другую) весьма сложно из-за отсутствия достаточно простого математического аппарата решения треугольников на эллипсоиде. Поэтому для решения навигационных задач чаще используют сферу, на которую должна быть спроектирована поверхность земного эллипсоида. Правило проекции должно обеспечивать требуемую точность вычислений, и, очевидно, не может быть однозначно для решения разных задач. Основным требованием является получение при проекции сплошного изображения без разрывов и складок. Но это условие приводит к искажению изображения отдельных частей проецируемой поверхности за счёт несоответствия длин отрезков и углов между ними их действительным величинам.

Гравитационное поле Земли

Поверхность геоида является эквипотенциальной поверхностью сил земного тяготения, состоящих из гравитационной и центробежной сил. Силы гравитации неотличимы от сил инерции, и поэтому, если их заранее не скомпенсировать, например, в системах, использующих в качестве датчиков исходной информации силовые акселерометры, то это приведет к ошибке измерения действительного ускорения, с которым движется объект.

Гравитационное поле является потенциальным полем, для его описания удобно воспользоваться понятием гравитационного потенциала U, дифференциал которого dU по своему физическому смыслу является работой, затрачиваемой для перемещения материальной точки с единичной массой на расстояние dr в рассматриваемом гравитационном поле. Вектор напряженности гравитационного поля g связан с потенциалом выражением

g = gradU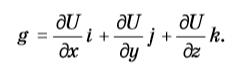

или в прямоугольной системе координат Oxyz
Для сферического тела с равномерно распределенной массой потенциал гравитационного поля определяется следующим образом: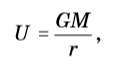




где M — масса Земли (притягивающего тела); G — универсальная гравитационная постоянная; r — расстояние от центра тела до заданной точки.

Вектор гравитационной силы проходит в этом случае через заданную точку и центр Земли, и это направление носит название геоцентрической вертикали.

В действительности Земля не является сферой, и масса ее по объему распределена неравномерно. Поэтому точное аналитическое описание ее гравитационного поля практически невозможно. Так же как и при описании формы Земли, здесь используются различные модели.

Физически определить можно только направление вертикали места (линии отвеса), совпадающее с направлением силы тяжести (см. рис. 1), в которую помимо гравитационной силы входит центробежная сила за счет вращения Земли. Это направление перпендикулярно к поверхности геоида. Если в модели учитывать только сплюснутость Земли, то направление силы тяжести совпадает с перпендикуляром к референц-эллипсоиду и определяет так называемую геодезическую вертикаль. Расхождение геодезической вертикали и вертикали места определяется уклонением вертикали, не превосходящей (0,1—0,3)10^-3 рад. Если можно пренебречь уклонением вертикали, то геодезическую вертикаль и вертикаль места часто объединяют под общим понятием географической вертикали.

Неравномерное распределение масс вблизи поверхности Земли не позволяет определить направление отвеса теоретически. Близость горы (не учитываемой поверхностью геоида) заставляет отвес отклоняться в ее сторону тем больше, чем больше ее масса и чем ближе к ней проводятся измерения. Наоборот, менее плотные породы среди более плотных оказывают как бы отталкивающее влияние на отвес. Обычно аномалии земной поверхности учитываются с помощью навигационных карт в автоматизированном режиме полета, а в автоматическом режиме — при помощи интерполяционных формул, полученных на основе экспериментальных исследований.

Движение Земли и системы измерения времени

Движение Земли в инерциальном пространстве включает в себя следующие составляющие: суточное вращение вокруг своей оси, годовое движение вокруг Солнца, прецессию оси, движение вместе с солнечной системой.

Угловая скорость вращения Земли вокруг своей оси составляет 15,04107°/час, нестабильность которой оценивается величиной 10^-8. Вокруг Солнца Земля движется по эллиптической орбите с максимальной скоростью 57,2’ в сутки в афелие (152 000 000 км в июле). Среднее расстояние от Земли до Солнца равно 149500000 км при эксцентриситете эллипса орбиты 0,01673, средняя скорость — 30 км/с. Перемещаясь по орбите вместе с Землей, наблюдатель, не ощущая своего собственного движения, видит перемещение Солнца относительно звезд. Большой круг небесной сферы, т. е. сферы произвольного радиуса с центром в точке наблюдения, по которому происходит годовое видимое движение Солнца, называется эклиптикой. Ось суточного вращения Земли наклонена к плоскости орбиты годового вращения Земли под углом 66°33’. Поэтому угол между плоскостью эклиптики и плоскостью небесного экватора составляет 23°27’. Небесный экватор (пересечение плоскости небесного экватора с небесной сферой) пересекается с эклиптикой в точке весеннего ϒ (21 марта) и осеннего Ω (23 сентября) равноденствия. При движении по эклиптике за полный оборот Солнце проецируется последовательно на двенадцать созвездий, образующих пояс Зодиака. Так как Земля не является сферой, то силы тяготения Солнца и Луны создают момент, стремящийся повернуть ось вращения Земли, что приводит к ее прецессии. Ось вращения Земли описывает от востока к западу коническую поверхность вокруг перпендикуляра к плоскости орбиты с периодом около 25800 лет. Из-за прецессии точки весеннего и осеннего равноденствия смещаются за год на 57,25’.

Кроме прецессии ось Земли совершает короткопериодические колебания, самое значительное из которых имеет период около 18,6 года и амплитуду угловых отклонений около 7—9".

Вместе с солнечной системой Земля совершает спиралевидное движение, производя один оборот вокруг центра галактики за 180 млн лет с тангенциальной скоростью около 250 км/с.

Обеспечение безопасности и регулярности полетов невозможно без хорошо организованной единой службы времени. Для измерения времени пользуются наиболее стабильными естественными или искусственно создаваемыми периодическими процессами. Вращение Земли вокруг своей оси и движение Земли вокруг Солнца дают две основные единицы измерения времени — сутки и год.

Звездными сутками называют промежуток времени между двумя последовательными верхними кульминациями точки весеннего равноденствия (кульминация — прохождение через небесный меридиан), а за начало отсчета местного звездного времени S принимают момент ее верхней кульминации. Звездные сутки разбиты на звездные часы, минуты, секунды, которые могут быть выражены в угловой мере, исходя из того, что 24 часа соответствуют 360°. Вследствие смещения точки весеннего равноденствия из-за прецессии земной оси звездные сутки короче периода вращения Земли вокруг своей оси на 0,0084 с. Точка весеннего равноденствия на небесной сфере ничем не отмечена, поэтому непосредственное измерение звездного времени невозможно. Обычно звездные хронометры проверяют по верхней кульминации какой-либо звезды, положение которой относительно точки весеннего равноденствия, определяемое прямым восхождением α, известно. Тогда для момента верхней кульминации S = α, а в любой другой момент S = α + t, где t — местный часовой угол звезды.

Если звездное время определяется на начальном, гринвичском меридиане, то это время называют гринвичским временем (обозначается S).

Звездным годом называется промежуток времени между двумя последовательными прохождениями центра Солнца через одну и ту же точку небесной сферы, и он равен 365,2564 средних суток. Промежуток времени между последовательными прохождениями центра Солнца через точку весеннего равноденствия называется тропическим годом, и он равен 365,2422 средних суток.

Звездное время широко используют в авиационных навигационных системах, так как звездные сутки практически постоянны, а способы его определения достаточно просты. Однако для повседневного использования звездное время неудобно, так как оно не связано с Солнцем, которое перемещается относительно звезд примерно на 1° в сутки. Таким образом, звездные сутки короче солнечных примерно на 4 мин. Вследствие этого начало звездных суток смещается: например, весной оно будет ночью, а зимой днем. Так как вся деятельность человека тесно связана с естественной освещенностью, то целесообразно измерение времени производить по Солнцу.

Истинными солнечными сутками называется промежуток времени между двумя последовательными нижними кульминациями центра солнечного диска на одном и том же географическом меридиане. Время, прошедшее от момента нижней кульминации Солнца (истинная полночь) до любого другого его положения, выраженное в долях истинных солнечных суток (часах, минутах, секундах), называется истинным солнечным временем T_Θ, которое в любой момент равно часовому углу Солнца t_Θ, выраженному в единицах времени, плюс 12 ч. Однако вследствие неравномерного движения Солнца по эклиптике и наклона эклиптики к экватору истинные солнечные сутки имеют разную продолжительность в течение года: максимальная разница в продолжительности истинных солнечных суток примерно 51 с.

Для устранения этого неудобства введено понятие среднего Солнца и солнечного времени. Среднее Солнце — это фиктивная точка на небесной сфере, равномерно движущаяся по небесному экватору (а не по эклиптике) и совершающая полный оборот за тропический год. Средними солнечными сутками называют промежуток времени между двумя последовательными нижними кульминациями среднего Солнца. Их продолжительность совпадает со средней продолжительностью истинных солнечных суток за год. Среднее время T_m на данном меридиане равно часовому углу t_m среднего Солнца, выраженному в единицах времени, плюс 12 ч:

T_m = t_m + 12 ч.

Среднее время, так же как и звездное, не может быть измерено непосредственно, и его определяют через истинное солнечное время. Разность между средним и истинным солнечным временем в один и тот же момент называется уравнением времени E = T_m — T_Θ откуда T_m = T_Θ + E. Зная величину E и измерив T_Θ, можно определить T_m. Величины E вычисляются с достаточно высокой точностью и могут быть заданы графически, таблично или в виде интерполяционных формул. Разность истинного и среднего солнечного времени четыре раза в году равна нулю, а в течение года лежит в пределах от —26,4 до +14,4 мин. Время, измеренное на данном географическом меридиане, одинаковое для всего меридиана, называется местным временем. Пользование им создает значительные неудобства, что привело к появлению в 1870 году поясного времени. Система поясного времени предусматривает разделение всей земной поверхности меридианами на 24 пояса по 15° каждый. За средний меридиан начального, нулевого пояса принят гринвичский. На территории всего часового пояса устанавливается единое время, равное местному среднему солнечному времени среднего меридиана данного часового пояса T_n. Для удобства пользования поясным временем границы часовых поясов проходят не строго по меридианам, а по государственным, административным границам или естественным рубежам.

Навигационные системы координат

Большое количество решаемых в навигации задач, а также разнообразие датчиков навигационной информации определяют большое число используемых систем координат (СК). Применяемые СК должны обеспечивать: решение навигационных задач с требуемой точностью, охват необходимой по площади территории единой системой координат, наглядную информацию о местоположении летательного аппарата (ЛА), получение наиболее простых способов программирования заданных маршрутов с малыми затратами времени. В зависимости от масштабов перемещений ЛА системы координат можно разделить на глобальные, местные и астрономические.

Глобальные СК жестко связаны с Землей и применяются для навигации, охватывающей всю земную поверхность или значительную ее часть. Наиболее распространенными глобальными СК являются: геодезическая (географическая), нормальная сферическая (геоцентрическая), ортодромическая, полярная и биполярная.

Геодезическая система координат

В качестве навигационной системы координат (НСК) используется географическая (геодезическая) система координат (см. ГОСТ 51794-2008) – система параметров, два из которых (геодезическая широта В и геодезическая долгота L) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий параметр (геодезическая высота Н) представляет собой высоту точки над поверхностью отсчетного эллипсоида (см.рис.5)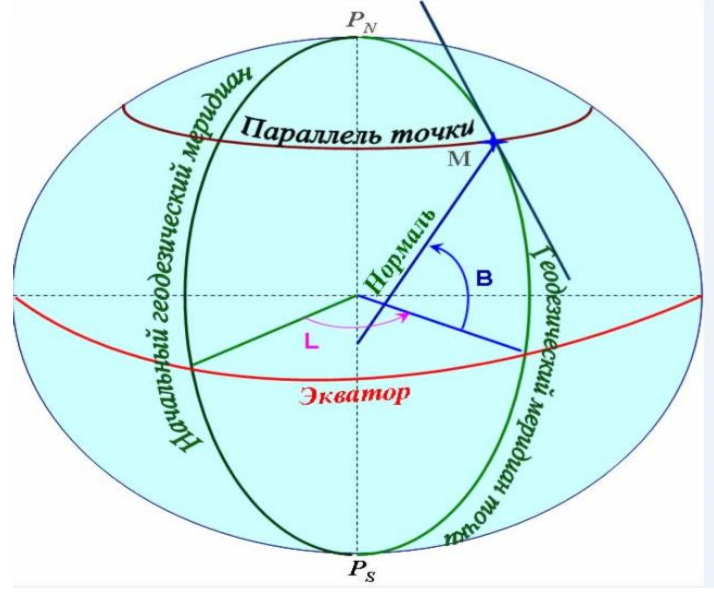

В геодезической СК в качестве модели Земли используется общеземной эллипсоид (типа WGS-84 или ПЗ-90), а за основную плоскость отсчета принимается плоскость экватора (рис. 3). Положение точек на поверхности эллипсоида определяется геодезическими координатами: геодезической широтой B и геодезической долготой L.
Рис.5. Геодезическая система координат

Геодезической широтой B точки М называется угол между нормалью к поверхности эллипсоида, т. е. геодезической вертикалью в этой точке, и плоскостью экватора. Широта отсчитывается от плоскости экватора к полюсам: от 0 до +90° в направлении северного полюса P_N, и от 0 до —90° в направлении южного полюса P_S.

Геодезической долготой L точки М называется двугранный угол между плоскостями начального (гринвичского) меридиана и меридиана данной точки. Долгота измеряется либо центральным углом в плоскости экватора, либо дугой экватора в пределах от 0 до 360°.


Пространственные прямоугольные координаты.

Начало системы координат (см.рис.6) расположено в центре O земного эллипсоида.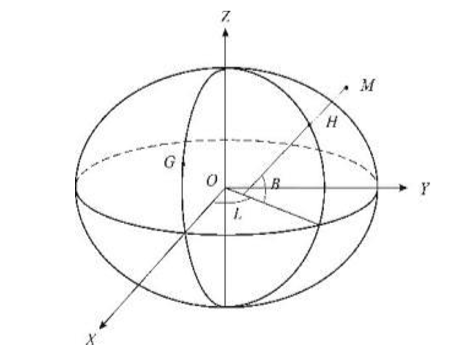





Рис. 6. Земной эллипсоид и координаты: Хо, Yо , Zо – пространственные прямоугольные; B, L, H - геодезические; G – Гринвичский меридиан

Сопровождающий трехгранник (СТ) ОЕNH навигационной (геодезической) системы координат (НСК) является модификацией нормальной системы координат ОХ_gY_gZ_g (ГОСТ 20058-80).

Примечание: Нормальная система координат (ГОСТ 20058-80) – подвижная система координат, в которой ось ОY_g направлена вверх по местной вертикали, а направление осей ОХ_g и ОZ_g - выбирается в соответствии с задачей. В данном случае СТ НСК модифицирована только с точки зрения вертикали (не местная, а геодезическая).

Начало отсчета СТ совпадает с текущим положением измерительного центра системы (ИЦ).

Оси СТ ориентированы следующим образом:

• 
  ось ОN направлена на Север параллельно касательной к геодезическому (географическому) меридиану в точке местонахождения ИЦ;
  
• 
  ось ОН направлена вверх по геодезической вертикали;
  
• 
  ось ОЕ образует с осями ОN и ОН правый трехгранник (т.е. направлена на Восток).
  

Связанная система координат объекта

Связанная система координат ОХУZ (ГОСТ 20058) – подвижная система координат, направления осей которой (продольной, нормальной и поперечной) фиксировано относительно объекта. Продольная ось ОХ направлена от хвостовой к носовой части объекта и располагается в плоскости симметрии объекта или плоскости параллельной ей (если начало координат помещено вне плоскости симметрии). Нормальная ось OY направлена к верхней части фюзеляжа объекта и располагается в плоскости симметрии объекта или плоскости параллельной ей (если начало координат помещено вне плоскости симметрии). Поперечная ось OZ перпендикулярна плоскости симметрии объекта и направлена к правой части объекта.

В задачах микронавигации начало ССК объекта полагается находящимся в плоскости симметрии объекта и в расчетном центре масс объекта.
Остановленная горизонтированная система координат (ГСК)

Остановленная горизонтированная система координат (ГСК) является разновидностью земной системы координат (ГОСТ 20058-80), т.е. правой прямоугольной декартовой системы координат, начало О₀ и оси которой фиксированы по отношению к Земле и выбираются в соответствии с задачей.

В задачах навигации ГСК О_гХ_гY_гZ_г начало отсчета совпадает с положением измерительного центра в момент назначения ГСК, а направления осей зафиксированы в момент назначения ГСК по отношению к Земле и ориентированы следующим образом:

• 
  направление оси О_гY_г совпадает направлением оси ОН сопровождающего трехгранника НСК в момент назначения ГСК (т.е. с направлением вверх по геодезической вертикали);
  
• 
  направление оси О_гХ_г совпадает с направлением горизонтальной проекции продольной оси связанной системы координат (ССК) объекта в момент назначения ГСК;
  
• 
  направление оси О_гZ_г совпадает с направлением горизонтальной проекции поперечной оси ССК объекта в момент назначения ГСК.