Информационные процессы и системы синергия. ответы тут. Тема Основные концепции и понятия теории информационных процессов и систем Цели изучения темы познакомиться с понятиями информационная система
 Скачать 1.18 Mb.
|
|
Тема 6. Моделирование потоков работ в информационных системах Цели изучения темы: познакомиться с концепцией потока работ и подходами к анализу и проектированию систем, основанных на концепции потока работ. Задачи изучения темы: познакомиться с концепцией потока работ; познакомиться с наиболее известными методологиями моделирования потока работ; познакомиться с моделями, позволяющими проводить анализ и оптимизацию потоков работ. Успешно изучив тему, Вы: Получите представление о: области применения подхода, основанного на концепции потока работ; преимуществах подхода к построению систем, основанного на концепции потока работ; современных достижениях в области методического обеспечения создания систем, основанных на концепции потока работ. Будете знать: основные понятия теории сетей Петри; возможности сетей Петри для моделирования информационных процессов; назначение и сущность метода критического пути и метода; назначение и сущность метода PERT. Вопросы темы: 1. Концепция потоков работ. 2. Моделирование на основе сетей Петри. 3. Высокоуровневые сети Петри. 4. Модель сетевого планирования. Вопрос 9. Концепция потоков работ. В процессе стремительного развития и применения достижений информационных технологий, в первую очередь, в таких областях как электронная коммерция, возникла необходимость построения новой концепции описания деловых процессов. Одной из таких концепций, получивших широкое распространение, стала концепция потока работ. Например, чтобы обработать пользовательский запрос к системе бронирования авиабилетов через Интернет, системой реализуется довольно сложная процедура, в процессе которой (согласно указанным в запросе параметрам - пункты и даты вылета и прилета, класс билета и их число) производятся обращения на сайты разных авиакомпаний. На основании полученных сведений готовятся варианты с маршрутами, датами и временем вылета и прилета и стоимости билета, которые предлагаются пользователю. Процесс может еще более усложниться, если в запросе предусмотрено бронирование мест в гостинице или аренда автомобиля. Все выполняемые действия рассматриваются как отдельные работы, состав и логика выполнения которых описываются моделью потока работ. Основным органом, координирующим усилия по развитию работ в области моделирования потока работ, выступает основанная в 1993 году международная организация разработчиков, пользователей, консультантов и аналитиков Workflow Management Coalition (WfMC, http://www.wfmc.org/). В соответствии с определением WfMC поток работ (workflow, WF) есть полная или частичная автоматизация делового процесса, когда документы, информация или задачи передаются от одного участника другому для проведения с ними действий согласно установленному перечню правил. Система управления потоками работ (Workflow Management System - WFMS) представляет собой систему, которая определяет, создаёт и управляет выполнением потоков работ посредством программного обеспечения, работающего на одном или более механизмах исполнения потока работ (workflow engines) и которая в состоянии интерпретировать определения процессов, взаимодействовать с участниками потока работ и в нужных случаях прибегать к средствам ИТ и приложений. (WfMC). Система управления потоками работ назначает каждой работе исполнителей, контролирует прохождение работы и отслеживает степень её выполнения. Автоматизированные системы управления потоками работ позволяют: избежать потерь или «зависаний» работ, устраняя тем самым необходимость в участии диспетчеров или контроллёров; предоставить управленческому персоналу возможность уделить большее внимание задачам повышения производительности труда отдельных исполнителей и оптимизации деловых процедур, освободив от рутинных процедур распределения задач по исполнителям и проверки исполнения; обеспечить выполнение процедур в строгом соответствии с установленной последовательностью и обязательным документированием результатов, что гарантирует точное следование деловому плану и соблюдение требований; подобрать наиболее подходящего исполнителя (сотрудника или устройство) для выполнения каждой работы с учётом относительной важности отдельных работ и прецедентов; достичь по сравнению с традиционным подходом максимального распараллеливания (одновременного или попеременного) выполнения работ. В настоящее время среда WF встроена, в частности, в ряд продуктов Microsoft, таких Visual Studio, SharePoint PortalServer, Microsoft Outlook и Microsoft Exchange Server. Модель потока работ (workflow model) представляет собой модель повторяющихся последовательностей действий или операций реальной системы с целью их оценивания, анализа, реорганизации или преобразования. Применение таких моделей может помочь определить наиболее рациональный способ организации производственных процессов, процессов обслуживания или обработки информации. При проектировании программного обеспечения информационных систем, модели потока работ используются для построения человеко-машинного интерфейса. В типичном случае поток работ состоит из совокупности выполняющихся в логической последовательности единиц работ, называемых действиями, или активностями (activity, или task). Действие может представлять собой ручную операцию, взаимодействие с пользователем или участником потока работ, а также операцию, выполняемую автоматически. Действия растянуты во времени, они могут перемежаться и взаимодействовать между собой. Отдельные экземпляры действий образуют список работ (worklist). То, что вызывает действия или является их объектом, называется прецедент, или ситуация (case, или worklow instance). Например, в потоке работ системы управлением обработки заказов прецедент создается каждый раз, когда поступает очередной заказ. Прецедент может представлять собой как имеющий конкретное воплощение объект, так и некоторую абстракцию (например, строительный проект или заявление на выплату страхового возмещения). В системах управления потоками работ используется множество различных языков и концепций. В большинстве систем применяется свой собственный язык. Наряду с ними в последнее время все большее распространение получает подход на основе аппарата сетей Петри, который будет рассмотрен далее. В информационных системах, ориентированных на процессы, для спецификации потоков выделяются несколько перспектив (perspective). Согласно классификации образованной в 1999 году Workflow Patterns initiative (http://www.workflowpatterns.com/patterns/), ставящей своей задачей создание концептуальной основы для процессной технологии, в качестве перспектив выделяются: Перспектива потока управления (control-flow perspective). Фокусируется на зависимостях по управлению между различными задачами, например, параллельное выполнение работ, выбор из нескольких работ, синхронизация работ. Перспектива данных (data perspective). Имеет дело с передачей информации, областью видимости переменных и т.п. Перспектива ресурсов (resource perspective). Рассматриваются назначения ресурсов работам, их передача другим работам и т.п. Перспектива обработки исключительных ситуаций (exception handling perspective). Отображаются причины отклонений от нормального хода выполнения и действия по их устранению. Для каждой из перспектив создаются шаблоны (pattern). Всего на сегодняшний день создано около 100 шаблонов (для перспективы потока управления создано более 40 шаблонов) разной степени сложности. На Рис. 18 дано визуальное представление двух шаблонов (имеющих на сайте номера 1 и 2): Последовательность (Sequence) и Распараллеливание (Parallel Split).  а) 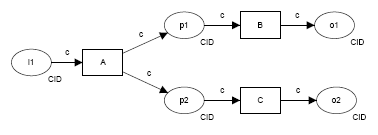 б) Рис. 18. Шаблоны Последовательность (а) и Распараллеливание (б) Последовательность (а) является базовым блоком для организации процессов. В этом случае работы выполняются последовательно одна за одной. Распараллеливание (б) означает что после завершения работы А инициируются два процессных потока так, что работы В и С могут выполняться одновременно. Шаблоны потоков работ и теория сетей Петри положены в основу языка YAWL (Yet Another Workflow Language – еще один язык потока работ), который был создан сотрудником Технологического университета г.Эйндховена (Голландия) Вилем ван дер Альстом (Wil van der Aalst) и сотрудником Квинслендского университета г.Брисбена (Австралия) Артуром Хофстеде (Arthur ter Hofstede) в 2002 году. Для языка разработана и поддерживается программная среда, которая свободно распространяется через Интернет (http://sourceforge.net/projects/yawl/) и состоит из нескольких компонентов для различных платформ. Для ознакомительных целей и изучения предназначен компонент YAWL4Study, который просто устанавливается и легко осваивается. На Рис. 19 показан вид интерфейса с редактором YAWLEditor, где показано описание потока работ для примера, который приводился в начале данного вопроса. 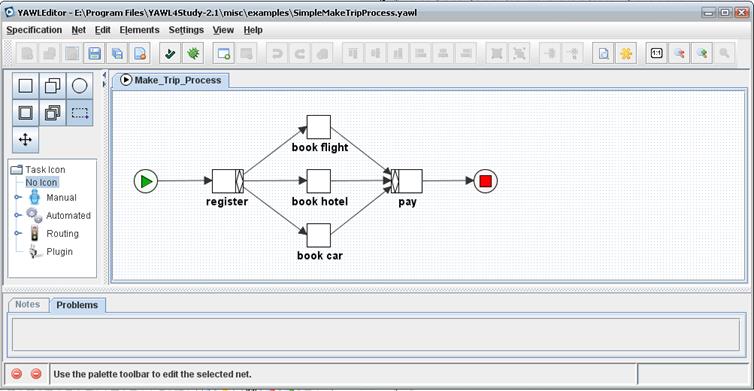 Рис. 19. Пример YAWLEditor Символы на рисунке имеют следующий смысл:
Вопрос 10. Моделирование на основе сетей Петри. Большими возможностями с точки зрения своего использования для моделирования деловых процессов и, в особенности, для моделирования потока работ обладают сеть Петри. Впервые теория сети Петри была предложена в 1962 году немецким исследователем Карлом Адамом Петри для моделирования и анализа систем с параллельно протекающими взаимодействующими процессами. Оригинальное изложение теории основано на применении строгого формального аппарата, что является важной отличительной стороной этой теории и выделяют её из других подходов к моделированию задач указанного класса. Несмотря на то, что математическая строгость является сильной стороной теории, более наглядной для объяснения её сути и более удобной для практического применения является её графическая интерпретация. В ней используется два основных понятия, с которыми связано представление процессов в системе: событие и условие. Событие есть некоторое наблюдаемое в системе действие, возникновение которого определяется множеством условий, представляющих собой логические высказывания (предикаты). Для наступления каждого из событий необходимо, чтобы было выполнено одно или несколько условий, называемых предусловиями. Факт наступления события может привести к тому, что будут выполнены другие условия, называемые постусловиями. Эти понятия реализованы элементами двудольного ориентированного графа, которым может быть представлена классическая сеть Петри. Напомним, что двудольным называется граф, в котором все множество вершин можно представить двумя непересекающимися подмножествами так, что вершины, соединенные дугой графа, всегда принадлежат разным подмножествам (см. Рис. 20): 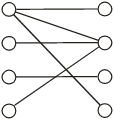 Рис. 20. Двудольный граф Вершины первого множества (будем их обозначать p) называются местами, или позициями (places) и изображаются графически в виде окружностей. Вершины второго множества (будем их обозначать t) называются переходами (transitions) и изображаются графически либо в виде толстых линий, либо в виде прямоугольников (будем далее использовать это обозначение). Вершины соединяются посредством направленных дуг. Соединяться могут вершины только разных типов. Например, на Рис. 21 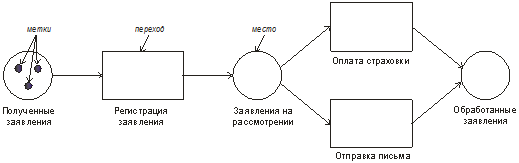 Рис. 21. Пример сети Петри показана модель процесса обработки в страховой компании заявлений на выплату страховой суммы после наступления страхового случая. В этом графе присутствуют три места - Полученные заявления, Заявления на рассмотрении, Обработанные заявления и три перехода - Регистрация заявления, Оплата страховки, Отправка письма. Места в графе подразделяются на входные и выходные. Место p называется входным для перехода t тогда и только тогда, когда существует дуга, направленная из t в p. Место p называется выходным для перехода t тогда и только тогда, когда существует дуга, направленная из p в t. Места могут содержать метки, или фишки, или маркеры (tokens), которые изображаются черными кружками и управляют переходами сети. Запускаться переход может только при условии, что каждое из входных мест содержит число меток, называемых разрешающими метками, не меньшее, чем число исходящих из места дуг. Переход в этом случае называется разрешенным. Так, на Рис. 21 разрешенным является переход Регистрация заявления, переходы Оплата страховки, Отправка письма запрещены. Сеть Петри представляет собой в общем случае мультиграф. На Рис. 22 показан пример сети, содержащей более одной дуги, которые соединяют входное место с переходом: 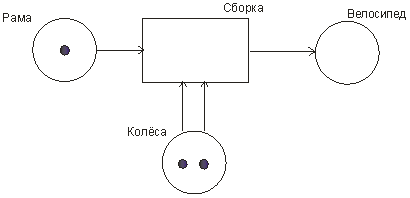 Рис. 22. Сеть Петри с множественными дугами Граф на Рис. 22 отражает тот факт, что для сборки велосипеда необходимо иметь раму и два колеса, на что указывает пара стрелок, идущих из входного места Колёса в переход Сборка. Для того, чтобы переход Сборка был разрешен, необходимо, чтобы входное место Колёса содержало две метки. Когда переход запускается, число используемых переходом меток определяется числом стрелок, входящих в этот переход. В каждый отдельный момент времени сеть однозначно характеризуется своим состоянием,называемым также маркировкой (marking), которое может быть задано перечислением числа меток, находящихся в каждом из мест сети. Например, состояние сети на Рис. 21 можно записать в виде вектора (3,0,0), или выражения [3p1 +0p2 +0p3], означающих, что место Полученные заявления (p1) содержит три метки, место Рассматриваемые заявления (p2) содержит ноль меток и место Обработанные заявления (p3) содержит ноль меток. Переход запускается, или срабатывает (fire) в результате удаления меток из входных мест и внесения меток в выходные места. Например, результатом срабатывания перехода Регистрация заявления на Рис. 21 будет граф, показанный на Рис. 23: 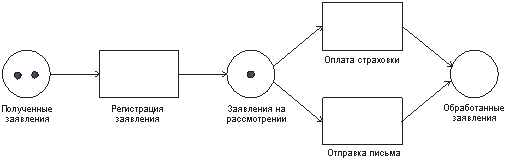 Рис. 23 Результат срабатывания перехода сети Петри Рис. 21 При моделировании деловые процессы отображаются на отдельные элементы сети Петри. К активным элементам сети Петри относятся переходы, срабатывание которых переводит сеть из одного состояния в другое. Переходы могут представлять отдельные операции делового процесса, такие как преобразования или транспортировка каких-либо объектов. К пассивным элементам сети Петри относятся места, которые не меняют состояние сети. Места могут представлять буферные накопители, среду хранения, физическое местонахождение, состояние обработки какого-либо объекта или условие, в котором он находится. Метки сети Петри представляют собой некоторые объекты, которые в зависимости от сущности моделируемой системы могут быть как физической, так и информационной природы. В расширенной сети Петри можно отразить наличие определённых ограничений на протекание процессов (деловых правил). Например, если вместо модели Рис. 22, которая допускает возможность одновременной сборки нескольких велосипедов, необходима модель, в которой будет отражено ресурсное ограничение, допускающее в каждый момент сборку не более одного велосипеда, то граф следует преобразовать в граф Рис. 24. 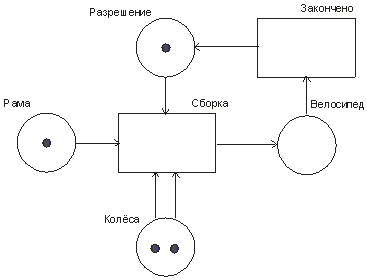 Рис. 24. Сеть Петри с ограничениями В преобразованном варианте в момент, когда очередной комплект компонентов поступит на сборочный участок, место Разрешение, запретит сборку очередного велосипеда. Эта возможность появится по окончании процесса сборки текущего экземпляра и появления метки в месте Разрешено после срабатывания перехода Закончено. Вопрос 11. Высокоуровневые сети Петри. Практическое использование теории сетей Петри довольно скоро привело к выводу об ограниченности её возможностей применительно к моделированию реальных систем. Этот вывод привел к созданию ряда расширений теории, ориентированных на решение этой задачи. Наибольший интерес для моделирования деловых процессов представляют раскрашенные сети Петри, временные сети Петри и высокоуровневые сети Петри, которые называются высокоуровневыми. Раскрашенные сети Петри позволяют преодолеть ограничения обычной сети Петри, вызываемые неразличимостью меток. Так, в рассмотренной выше модели процесса обработки заявлений на выплату страховой суммы (Рис. 21) невозможно отобразить такую, например, характеристику, как величина возмещаемой суммы, что может быть существенным для применения процедурных правил работы с заявлением. Возможность наделить метки набором значений определённых признаков обеспечивается приданием метке «цвета», в котором могут храниться все нужные для применения деловых правил значения. Запуск перехода осуществляется на основе проверки не только наличия меток во входных местах, но и на основе учета значений входных меток. Иначе говоря, предусловие может быть сформулировано более детально. Кроме того, в раскрашенных сетях Петри от значений входных меток зависят как число получаемых выходных меток, так и значения, которые им должны быть присвоены. Временные сети Петри реализует возможность осуществить привязку присутствующих в них событий к временному параметру с помощью временной отметки, или веса (timestamp), которые получает метка в дополнение к своим значениям. Например, значение временной отметки равное 12 будет означать, что метка будет доступна для поглощения в момент времени 12. Переход считается разрешенным в случае, если все метки во входных местах имеют в качестве значений своих временных отметок значения, не превышающие текущего времени. Метки изымаются в соответствии с дисциплиной «первый пришел - первый обслужен», т.е., первой изымается метка с минимальным значением временной отметки. При срабатывании перехода выходные метки получают значения временных отметок не меньшие, чем момент времени срабатывания перехода, увеличенный на время задержки. Величина задержки в общем случае зависит от значений изымаемых входных меток, но может быть и величиной постоянной или случайной. На Рис. 25 представлено описание с помощью сети Петри работы отдела технического обслуживания компьютерного класса, состоящего из n компьютеров (вместо меток в месте Компьютерный класс стоит обозначение n), каждый из которых может выходить из строя. 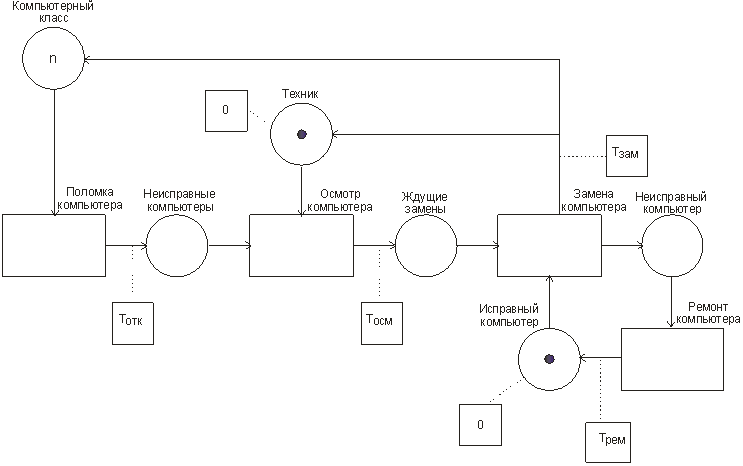 Рис. 25. Временная сеть Петри Сопровождение осуществляет один техник, который после поступления заявки пользователей проводит осмотр и проверку отказавшего компьютера, заменяет его исправным из резерва и отправляет отказавший в ремонт. Отремонтированный компьютер возвращается в резерв, на котором в начале процесса есть один исправный компьютер. Как видно из графа, переход Поломка компьютера будет разрешен, во входном месте Компьютерный класс есть метки. Чтобы отразить тот факт, что компьютеры выходят из строя по прошествии некоторого времени, возле перехода на графе поставлена временная отметка Тотк, представляющая собой значение среднего времени между двумя последовательными поломками (наработка на отказ). Переход Диагностика компьютера, возможный при наличии меток в местах Неисправные компьютеры и Техник свободен, будет запущен с временной задержкой Тосм, равной среднему времени осмотра и проверки. Аналогичным образом, переход Ремонт компьютера, возможный при наличии метки в месте Исправный компьютер будет запускаться с задержкой на время ремонта Трем, переход Замена компьютера будет запускаться с задержкой Тзам. Метки Техник и Исправный компьютер доступны для использования в момент начала моделируемого процесса. Раскрашенные и временные сети Петри позволяют создавать модели довольно сложных процессов, но они не позволяют выявить их структуру. Такую возможность предоставляют иерархические сети Петри. Для представления процессов в укрупненном виде в сеть Петри добавляется элемент, называемый процесс, который обозначается прямоугольником с двойной граничной линией. Например, если мы ходим детализировать переход Ремонт компьютера на Рис. 25, то модель может быть преобразована в вид, показанный на Рис. 26 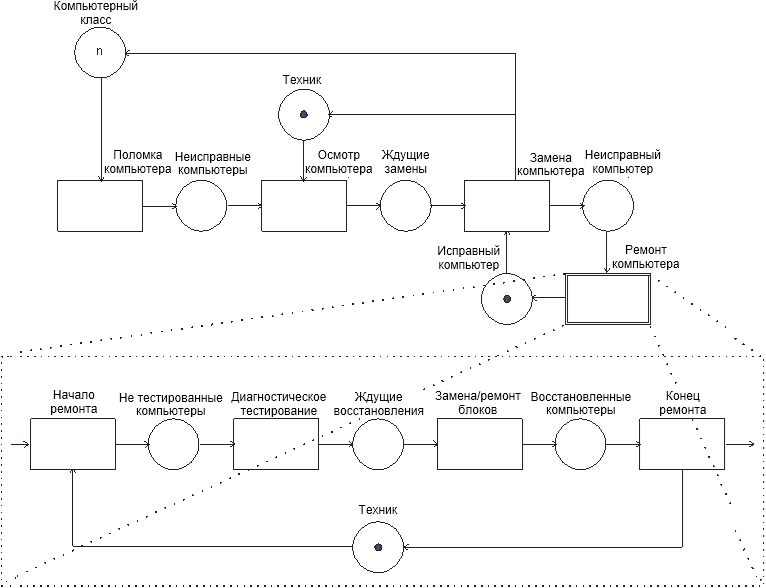 Рис. 26. Иерархическая сеть Петри Представленный как отдельный подпроцесс переход Ремонт компьютера включает теперь этапы Начало ремонта, Диагностическое тестирование, Замена/ремонт блоков, Конец ремонта. При этом число компьютеров, которые могут ремонтироваться одновременно, ограничено одним. Концепция иерархических сетей Петри реализует один из основополагающих принципов системного подхода: систематически применяя принцип декомпозиции процесса на подпроцессы можно значительно упростить анализ в сложных случаях. Кроме того, появляется возможность использовать модели отдельных процессов многократно - в случаях, когда он как подпроцесс встречается в нескольких местах создаваемой модели. Однако непосредственное применение теории сетей Петри для моделирования потока работ сталкивается с рядом проблем, к которым относятся следующие: Раскрашенные сети Петри дают возможность представить несколько реализаций подпроцессов. Однако, средств моделирования их взаимодействия таких, как трассировка, ветвление и слияние реализаций не предусмотрено. В процессе анализа часто возникает необходимость слияния потоков, относительно которых неизвестно, какой вид синхронизации необходим. Если активными являются оба потока, требуется AND-соединение, в противном случае XOR- соединение. Моделировать предварительную синхронизацию для таких ситуаций в модели сети Петри довольно трудно, поскольку правило запуска требует задавать определённый вид соединения (AND-соединение для переходов и XOR- соединение для мест). Запуски переходов разрешаются своими входными местами и изменяют только свои выходные места. Однако эффект наступления некоторых событий, связанных с потоком работ, может выходить за рамки локального. Так, может возникнуть необходимость удалить ошибочные метки из всех мест, где они в данный момент находятся, или реализовать действия, которые требуется принять по истечении контрольного срока. Поэтому для представления моделей в системах управления потоками работ используют сети Петри в адаптированном виде. Вопрос 12. Модель сетевого планирования. Сеть Петри может быть легко преобразована в сетевую модель, которая вместе со связанным с нею методом критического пути появилась в конце пятидесятых годов прошлого века, и находит широкое применение для задач планирования. С ее помощью могут решаться как задачи проектирования информационных систем, так и задачи оптимальной организации потока работ в процессе их моделирования. Сетевая модель (см. пример Рис. 27) базируется на теории ориентированных графов. 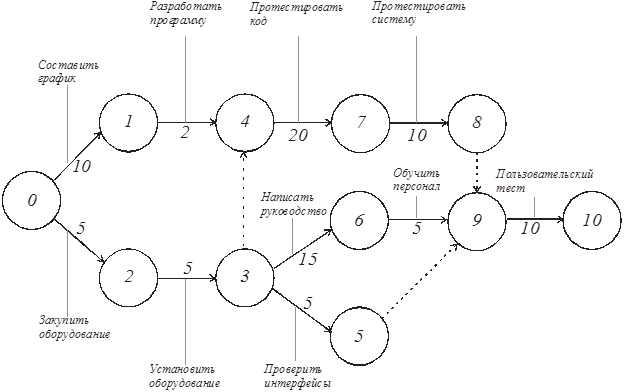 Рис. 27. Пример сетевой модели Основными элементами модели являются событие, работа и путь. Событие (nod) - факт завершения всех предшествующих работ и готовности к выполнению всех последующих. Исходное событие (не имеющее входящих дуг) сети называется начальным, или истоком и обычно обозначается 0, завершающее событие (не имеющее исходящих дуг) называется конечным, или стоком. Работа (task) есть активность, связанная с расходованием ресурсов. Работа определяется своими начальным (i) и конечным (j) событиями. Основным ресурсом, связанным с работами является время ее выполнения, по причине чего на графе проставляются пометки со значениями длительности выполнения работы, выраженной в условных единицах (см. Рис. 27). Работы, показанные на графе Рис. 27 пунктиром, называются фиктивными – они имеют нулевую длительность (пометка 0 обычно не ставится), но необходимы для отражения логической последовательности работ. Например, присутствие фиктивной работы (3,4) означает, что работа (4,7) может начаться после завершения не только работы (1,4), как это было бы в случае отсутствия работы (3,4), но и работы (2,3). Все события (вершины графа) номеруются так, чтобы соблюдалось следующее правило: номер начального события каждой работы должен быть меньше номера ее конечного события. Путь (path)– последовательность работ в сети, в которой конечное событие любой работы совпадает с начальным событием следующей за ней работы. Путь, имеющий наибольшую продолжительность, называется критическим (critical path) Lкр, его длительность обозначается Tкр. Время выполнения процесса (проекта) в целом не может быть меньше Tкр, поэтому первая задача при анализа сетевой модели состоит в нахождении Lкр и критических работ и поиск возможностей по сокращению их длительности. На этом базируется и в этом состоит сущность метода критического пути(Critical Path Method - СРМ). Дадим описание этого метода на примере модели, показанной на Рис. 28, ограничившись решением упрощенной задачи нахождения только величины критического пути. 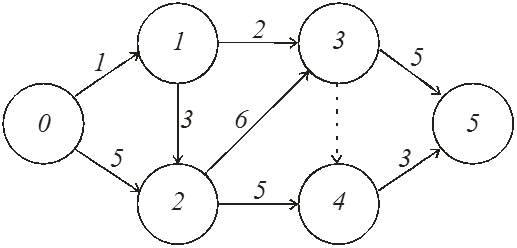 Рис. 28. Пример нахождения критического пути Для нахождения критического пути будем последовательно определять наиболее ранние моменты наступления событий t(i), начиная с начального (i=0). Событие 0. Естественно считать, что событие 0 наступает в момент времени равный 0: t(0)=0. Событие 1. Поскольку в событие 1 входит только одна работа (0,1), то событие 1 наступит тогда, когда завершится работа (0,1). Так как она началась в нулевой момент, то время ее завершения равно ее продолжительности, т.е., t(1)=1. Событие 2. Событие 2 наступит после завершения работ (0,2) и (1,2). Первая из них начинается в момент t(0)=0 и длится 5 единиц времени, вторая – в момент t(1)=1 и длится 3 единицы времени. Таким образом, работа (0,2) закончится в момент (0+5)=5, работа (1,2) – в момент (1+3)=4. Событие 2 наступит тогда, когда завершатся обе работы, т.е., в момент t(2)=max(5,4)=5. Событие 3. Событие 3 наступит после завершения работ (1,3) и (2,3). Первая из них начинается в момент t(1)=1 и длится 2 единицы времени, вторая – в момент t(2)=5 и длится 6 единиц времени. Таким образом, t(3)=max(1+2,5+6)= max(3,11)=11. Событие 4. Событие 4 наступит после завершения работ (3,4) и (2,5). По аналогии с предыдущим получаем t(4)=max(11+0, 5+2)= max(11,7)=11. Событие 5. Событие 5 – конечное, для него t(5)= max(11+5,11+3)= max(16,14)=16. Таким образом, максимально быстро весь процесс может закончиться за время Tкр=16. Полное описание метода, который помимо длины критического позволяет определить сам критический путь, а также параметры событий и работ, можно найти в литературе, рекомендованной для изучения темы. Однако в реальности имеет место неопределенность как в структуре графа (те или иные события или работы могут присутствовать или же нет), так и во временных параметрах - времена выполнения работ, моменты наступления событий, резервы и пр. Поэтому для практических случаев применяются другие методы, одним из которых является метод PERT (Program Evaluation and Review Technique), относящийся к аналитическим методам и позволяющим получить значения вероятностных параметров модели при условии соблюдения некоторых ограничений. Метод, в частности, предполагает, что продолжительности работ t(i,j) подчиняются так называемому β-распределению с одинаковыми значениями параметров и такими, что средние  и дисперсии длительностей работ могут быть приближенно рассчитаны по формулам: (1),и  (2).где и означают минимальную и максимальную продолжительности выполнения работ. Кроме того, предполагается, что длительности работ независимы, а средняя величина критического пути существенно превосходит длительности прочих полных путей. Порядок расчета вероятностной модели методом PERT таков. 1) Вершины графа нумеруются. 2) Для каждой работы находятся оценки и . 3) Определяются математическое ожидание и дисперсия длительностей работ.4) На основании совокупности значений проводится обычный расчет характеристик, как для детерминированной сетевой модели.5) Определяется критический путь и его среднее значение. 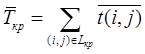 .6) Определяется дисперсия длительностей как сумма дисперсий длительностей критических работ (предположение о независимости работ).  .7) Поскольку длительности – независимые случайные величины, их сумму можно считать случайной величиной, распределенной по нормальному закону 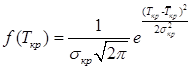 со средним и дисперсией , для которого функция плотности вероятности имеет вид: .8) Из свойств нормального распределения следует (правило «трех сигма»), что с вероятностью 0,9974 значение будет находиться в интервале  ,Поэтому можно утверждать, что  , .9) Если определен некоторый плановый срок выполнения всей совокупности работ (проекта) , то вероятность 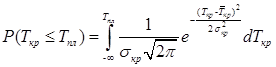 выполнения в этот срок всей совокупности работы определяется следующим образом: (3).Чтобы найти значение функции нужно перейти от 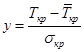 к стандартному распределению  . Для этого осуществляется замена переменной: (4).что приводит к изменению подинтегральной функции и пределов интегрирования: 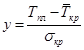 ; ;  ; ; ;y=0; .Тогда 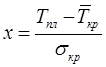 (5),и  .где Ф(х) называется функцией Лапласа. Значение функции можно получить с использованием библиотечных функций, которые присутствуют во многих компиляторах и программных пакетах. Проиллюстрируем применение метода на примере сетевой модели Рис. 28, в которой значения и для каждой работы указаны через точку с запятой, а вычисленные значения показаны жирным шрифтом (Рис. 29). 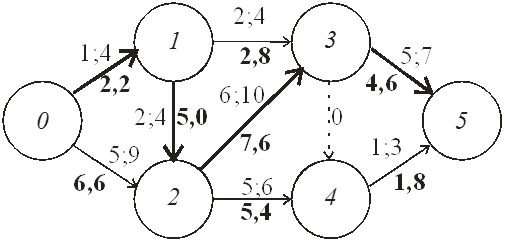 Рис. 29. Пример расчета методом PERT В соответствии с методом по формуле (1) находим средние значения работ. Например,  , .критический путь  (отмечен на Рис. 29 жирной линией)и его величину  .По формуле (2) вычисляются дисперсии работ критического пути 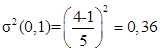 , ,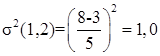 , 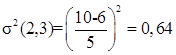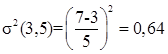.Дисперсия  .и среднее квадратичное отклонение  .критического пути. Определяются граничные значения критического пути  , .(иначе говоря, с вероятностью 0,9974 все работы будут выполнены в срок от 14,5 до 24,3 временных единиц). Оценим вероятность выполнения работы в срок для двух значений =20 и =17.Для этого по формуле (4) находим соответственно значения : 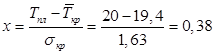 , .по которым определяем (например, с помощью функции НОРМСТРАСП программы Excel) значения вероятности:  , .Из практики известно, что если вероятность  , то проект спланирован с запасом, и даже избыточным. Величина  свидетельствует об угрозе срыва. Видим, что в нашем примере вероятность выполнить все работы в срок 17 временных единиц крайне низка.Другим возможным способом решить задачу является метод статистических испытаний, или метод Монте-Карло, который представляет собой универсальный метод решения многих задач и будет рассматриваться далее. В заключение обсуждения сетевой модели отметим, что наряду с возможностью преобразования модели, созданной на основе аппарата сетей Петри в сетевую модель, возможно и обратное преобразование: сетевая модель может быть легко преобразована в модель на основе сети Петри. Выводы: 1. Прогресс информационных технологий в ряде областей обусловил появление новой концепции организации и моделирования деловых процессов под названием поток работ. Построенные на базе данной концепции автоматизированные системы управления потоками работ позволяют получить ряд существенных выгод от их внедрения. 2. В настоящий момент не существует общепринятого стандарта формального описания потоков работ, поэтому проблема создания унифицированного и независящего от платформы языка моделирования потока работ остается актуальной и исследования в данном направлении продолжаются. 3. Для моделирования потока работ применяются различные методы. Одним из наиболее широко распространенных является подход на основе теории сетей Петри. Вместе с тем, как этот, так и другие подходы имеют ряд ограничений и нуждаются в расширении. 4. Для определения количественных характеристик моделируемых процессов можно использовать разработанные методы и модели, такие как модель сетевого планирования. Степень проработки ее формального аппарата дает возможность применять ее во многих практических ситуациях с достаточной точностью. Вопросы для самопроверки: 1. Что понимается под потоком работ? 2. Какие задачи решаются системой управления потоками работ? 3. Какие преимущества дает использование автоматизированных систем управления потоками работ? 4. Какие средства используются для моделирования потока работ? 5. Что представляет собой сеть Петри? 6. Какие основные объекты определяются в сети Петри? 7. Что такое места (позиции) в сети Петри? 8. Что бывают места в сети Петри? 9. Что такое переходы в сети Петри? 10. Что такое метки (фишки, маркеры) в сети Петри? 11. Что называется состоянием сети Петри и как оно задается? 12. Как реализуются ограничения в сети Петри? 13. Что позволяют описать и каким образом раскрашенные сети Петри? 14. Что позволяют описать и каким образом временныесети Петри? 15. Что позволяют описать и каким образом иерархическиесети Петри? 16. Что ограничивает применениетеориисети Петри для моделирования потока работ? 17. Что называется сетевой моделью? 18. Что понимается под событием? 19. Что называется работой? 20. Что такое фиктивная работа, и в каких случаях она нужна? 21. Что такое путь? 22. Какой путь называется критическим, каков его физический смысл? 23. Опишите логическую последовательность шагов нахождения величины критического пути на сетевом графе. 24. В чем могут состоять отличия между вероятностной и детерминированной сетевыми моделями? Литература по теме: Основная литература: 1. Шапкин А.С., Шапкин В.А. Математические методы и модели исследования операций: Учебник Издательство: Дашков и К, 2012. – То же [Электронный ресурс]. – URL: http://biblioclub.ru/. Дополнительная литература: 1. Wil van der Aalst. Workflow Management: Models, Methods, and Systems/ Wil van der Aalst and Kees Max van Hee-The MIT Press Cambridge, Massachusetts London, 2002 -368p. 2. Питерсон Дж. Сети Петри – М.: Мир, 1984 – 264с. 3. Кофман А., Дебазей Г. Сетевые методы планирования и их применение - М.: Прогресс, 1968. - 182 c. 4. Rob Allen. Workflow: An Introduction http://www.wfmc.org/View-document-details/Workflow-Interoperability-Enabling-E-Commerce-Rob-Allen.html?tmpl=component. 5. Шаблоны потоков работ http://www.workflowpatterns.com/. |
