Задание 1. Тема Задачи прогнозирования электропотребления
 Скачать 66.54 Kb. Скачать 66.54 Kb.
|
Практическое задание 1Распределение активной мощности между тепловыми электростанциями без учета потерь в сетиТема 2. Задачи прогнозирования электропотребления Задание Определите оптимальную загрузку двух тепловых электрических станций: ТЭС-1 (  ) и ТЭС-2 ( ) и ТЭС-2 ( ), работающих параллельно на одинаковом топливе. Расходные характеристики станции ), работающих параллельно на одинаковом топливе. Расходные характеристики станции  и и 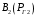 заданы по варианту (табл. 1.1). Нагрузка, на которую работают электрические станции, постоянна, т. е. не зависит от изменений мощности станций и задана в виде заданы по варианту (табл. 1.1). Нагрузка, на которую работают электрические станции, постоянна, т. е. не зависит от изменений мощности станций и задана в виде 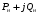 по варианту (табл. 1.1). Питание нагрузки осуществляется по воздушным линиям электропередачи: ЛЭП-1 и ЛЭП-2, от ТЭС-1 и ТЭС-2 соответственно согласно схеме, представленной на рис. 1.1. Потери мощности в ЛЭП не учитывать. Напряжения ЛЭП-1 и ЛЭП-2 одинаковы. по варианту (табл. 1.1). Питание нагрузки осуществляется по воздушным линиям электропередачи: ЛЭП-1 и ЛЭП-2, от ТЭС-1 и ТЭС-2 соответственно согласно схеме, представленной на рис. 1.1. Потери мощности в ЛЭП не учитывать. Напряжения ЛЭП-1 и ЛЭП-2 одинаковы.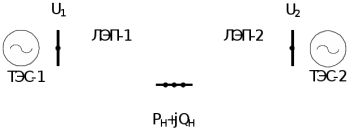 Рис. 1.1. Схема расчетной сети Рекомендации по выполнению практического задания 1Оптимальный режим ЭЭС – режим, соответствующий минимальному удельному расходу топлива на полезно отпущенный 1 кВт∙ч энергии. Расходная характеристика – часовой расход условного топлива в виде зависимости  , где , где 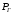 – мощность генерации. – мощность генерации.Характеристика относительных приростов (  ) – частная производная от расходной характеристики. ) – частная производная от расходной характеристики.Условие оптимальности работы электростанций – равенство относительных приростов. 1. Для заданных из условия задачи расходных характеристик станции определите характеристики относительных приростов станции как частные производные расходных характеристик по мощности станции:
где  – номер станции. – номер станции.2. Запишите условия оптимальности работы электрических станций. Так как обе станции работают на одинаковом топливе и потери мощности в сети не учитываются, а нагрузка не зависит от напряжения, то условие оптимальности работы электрических станций имеет вид:
3. Выразите мощность, генерируемую одной из тепловых станций, из условия оптимальности работы (уравнение с суммой мощностей генерации и нагрузки) и подставьте полученное выражение в уравнение равенства относительных приростов. 4. Приведите в полученном уравнении подобные члены и решите полученное уравнение с одним неизвестным. 5. Подставьте полученное значение в выражение, полученное в п. 3, и найдите мощность второй электростанции. Решение 1. Для заданных из условия задачи расходных характеристик станции определите характеристики относительных приростов станции как частные производные расходных характеристик по мощности станции:
где  – номер станции. – номер станции.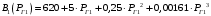 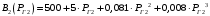 Найдем характеристики относительных приростов станций. 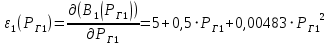 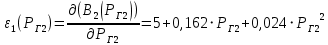 2. Запишите условия оптимальности работы электрических станций. Так как обе станции работают на одинаковом топливе и потери мощности в сети не учитываются, а нагрузка не зависит от напряжения, то условие оптимальности работы электрических станций имеет вид:
Условие оптимальности: 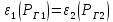  3. Выразите мощность, генерируемую одной из тепловых станций, из условия оптимальности работы (уравнение с суммой мощностей генерации и нагрузки) и подставьте полученное выражение в уравнение равенства относительных приростов.    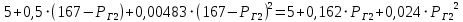 Раскроем скобки и приведем подобные:    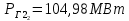 Находим  Ответ: 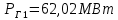 ; ;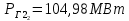 . .Таблица 1.1 Варианты к заданию 1
|

 ,
,
 , МВт
, МВт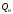 , Мвар
, Мвар