Правило Лопиталя. правило лопиталя. Теорема Лопиталя или правило Бернулли Лопиталя
 Скачать 66.82 Kb.
|
|
Теорема Лопиталя или правило Бернулли – Лопиталя – это метод нахождения пределов функций, раскрывающий неопределенности вида 0/0 и ∞/∞. Обосновывающая метод теорема утверждает, что при некоторых условия предел отношения функций равен пределу отношения их производных. Если: f(x), g(x) – действительнозначные функции, дифференцируемые в поколотой окрестности U точки a, где a – действительное число или один из символов +∞, -∞, ∞, причем 1. 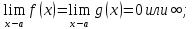 2.  3. существует  тогда существует  Пределы также могут быть односторонними. (действительнозначные функции – где переменная действительная) (односторонний предел – предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны).  Следствие Пусть функция f(x) дифференцируема в проколотой окрестности точки a, в самой этой точке она непрерывна и имеет предел производной  . Тогда функция f(x) дифференцируема и в самой точке a, и  (то есть производная  непрерывна в точке a).Для доказательства  |