самостоятельная работа геометрия 10 класс. геометрия 10 кл сам.раб. 19.01. Теорема о трех перпендикулярах

• Название: Теорема о трех перпендикулярах
• Анкор: самостоятельная работа геометрия 10 класс
• Дата: 24.03.2022
• Размер: 0.66 Mb.
• Имя файла: геометрия 10 кл сам.раб. 19.01.doc
• Тип: Документы; #413521

Задачи для самостоятельной работы по теме:

«Теорема о трех перпендикулярах»

1вариант

1. Угол C треугольника ABC- прямой. AD- перпендикуляр к плоскости треугольника ABC. Докажите, что треугольник BCD- прямоугольный.

2. ABCD- квадрат, диагонали которого пересекаются в точке E. AH- перпендикуляр к плоскости квадрата. Докажите, что прямые HEи BD перпендикулярны.

3. Из вершины A квадрата ABCD со стороной 16 см восстановлен перпендикуляр AE длиной 12 см. докажите, что треугольник BCE- прямоугольный. Найдите его площадь.

( )

4. Из центра O квадрата ABCD со стороной 18 см к его плоскости восстановлен перпендикуляр OM длиной 12 см. Найдите площадь треугольника ABM.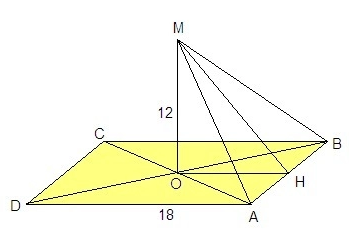
( Центр квадрата - точка О - точка пересечения диагоналей.
Диагонали квадрата равны и точкой пересечения делятся пополам:
ОА = ОВ.
Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные.
ОА - проекция МА на плоскость квадрата, ОВ - проекция МВ, значит
МА = МВ, т.е. ΔМАВ равнобедренный.
Пусть Н - середина АВ. Так как треугольник МАВ равнобедренный, то МН - его медиана и высота.
ОН = 0,5AD = 9 см как средняя линия ΔDAB.

ΔМОН: ∠МОН = 90°, по теореме Пифагора
               МН = √(МО² + ОН²) = √(144 + 81) = √225 = 15 см

Smab = AB · MH / 2 = 18 · 15 / 2 = 135 см²)

5. Отрезок AM перпендикулярен плоскости треугольника ABC и имеет длину 24 см. Найдите расстояние от точки M до прямой BC, если AB=AC=20 см., BC=24 см.
(треугольник АВС, АВ=АС=20, ВС=24, МА=24, проводим высоту АН=медиане, СН=ВН=ВС/2=24/2=12, проводим МН,треугольникАНС прямоугольный, АН=корень(АС в квадрате-СН в квадрате)=корень(400-144)=16, треугольник АМН прямоугольный, МН=корень(АМ в квадрате+МН в квадрате)=корень(576+256)= 8*корень13)

2вариант

1. Угол C треугольника МРC- прямой. МD- перпендикуляр к плоскости треугольника МРC. Докажите, что треугольник РCD- прямоугольный.

2. ABCD- квадрат, диагонали которого пересекаются в точке О. AH- перпендикуляр к плоскости квадрата. Докажите, что прямые HО и BD перпендикулярны.

3. Из вершины A квадрата ABCD со стороной 10 см восстановлен перпендикуляр AE длиной 16 см. докажите, что треугольник BCE- прямоугольный. Найдите его площадь.
(АВСД квадрат, АВ=10, ЕА перпендикулярна АВСД, треугольник АЕВ прямоугольный, ЕВ=корень((АВ в квадрате ЕВ в квадрате)=корень(256 100)=корень356=2*корень89, согласно теореме о трех перпендикяларах, если ЕА перпендикулярна АВ, а АВ перпендикулярна ВС, то ЕВ перпендикулярна ВС, уголЕВС=90, площадь ВСЕ=1/2ЕВ*ВС=1/2*2*корень89*10=10*корень89)

4. Из центра O квадрата ABCD со стороной 8 см к его плоскости восстановлен перпендикуляр OM длиной 10 см. Найдите площадь треугольника ABM
(Квадрат АВСД, АВ= 8 см, МО перпендикулярна (АВС), проведем высоту МН. Высота равна медиане на AB=1/2AD=8/2 = 4см.
МН = медиана на АВ. Треугольник HMA равнобедреный (AM=BM), треугольник НМО прямоугольный. МН=√(МО²+ОН²)=√(10²+4²)=√116=2√29 см
S(ABM) = 1/2 * 8*2√29=8√29 см²)

5. Отрезок AM перпендикулярен плоскости треугольника ABC и имеет длину 14 см. Найдите расстояние от точки M до прямой BC, если AB=AC=24 см., BC=20 см.