Цель деятельности учителя
|
Создать условия для рассмотрения теоремы об отрезках пересекающихся хорд и применения изученного материала при решении задач
|
Термины и понятия
|
Окружность, хорда, радиус, диаметр, дуга; хорда, стягивающая дугу окружности; вписанный угол
|
Планируемые результаты
|
Предметные умения
|
Универсальные учебные действия
|
Владеют базовым понятийным аппаратом по основным разделам содержания
|
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач.
Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач.
Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах.
Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
|
Организация пространства
|
Формы работы
|
Фронтальная (Ф); индивидуальная (И)
|
Образовательные
ресурсы
|
• Учебник.
• Задания для индивидуальной работы
|
I этап. Актуализация опорных знаний учащихся
|
Цель деятельности
|
Совместная деятельность
|
Повторить теоретический материал и выявить трудности, возникшие при выполнении домашнего задания
|
(Ф/И) Решить устно. Найти х.
|
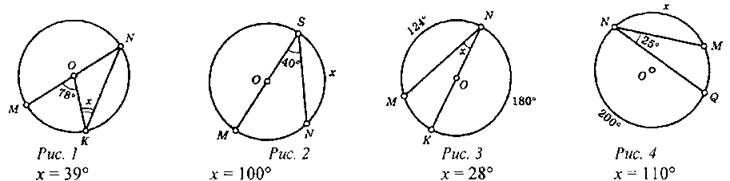
II этап. Мотивация к деятельности
|
Цель деятельности
|
Постановка учебной задачи
|
Подготовить учащихся к восприятию нового материала
|
(Ф/И) Решить задачу.
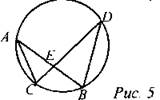
Доказать: ∆АЕС ∆DEB.
Найти: АЕ, если BE = 4 см; DE = 6 см, СЕ = 2 см
|
III этап. Изучение нового материала
|
Цель деятельности
|
Совместная деятельность
|
Вывести доказательство теоремы об отрезках пересекающихся хорд
|
Доказательство теоремы об отрезках пересекающихся хорд можно провести в виде задачи:
Докажите, что если две хорды АВ и CD окружности пересекаются в точке Е, то АЕ ∙ BE = СЕ ∙ DE.
Предложить решить задачу самостоятельно, а затем обсудить ее решение. В тетрадях и на доске записать план-конспект доказательства теоремы
|
IV этап. Закрепление изученного материала
|
Цель деятельности
|
Деятельность учителя
|
Деятельность учащихся
|
Совершенствовать навыки решения задач на применение теоремы о вписанном угле и ее следствий
|
(Ф/И)
Решить № 666 (а; б), 668, 670, 671 (а), 673. У доски можно выполнить № 668, 670
|
№ 668.
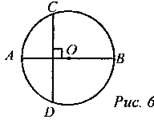
Дано: АВ - диаметр, CD ⊥ АВ, CD ∩ АВ = К.
Доказать: 
Доказательство:
1) Так как CD ⊥ АВ, по аналогичным рассуждениям в предыдущей задаче СК = KD.
2) По свойству хорд: АК ∙ КВ = СК ∙ KD, так как СК = KD, то АК ∙ КВ = СК2;  что и требовалось доказать.
№ 670.
Дано: АВ - касательная, AQ - секущая.
Доказать: АВ2 = АР ∙ AQ.
Доказательство:
Рассмотрим ∆АВР и ∆AQB: ∠A - общий, ∠B = ∠Q. ∆АВР ∆AQB (по двум углам), следовательно, 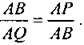 По свойству пропорции, АВ2 = АР ∙AQ, что и требовалось доказать
|
V этап. Итоги урока. Рефлексия
|
Деятельность учителя
|
Деятельность учащихся
|
(Ф/И)
- С какой теоремой познакомились на уроке?
- Закончите фразу:
• Было трудно...
• Я выполнял задания...
• Я понял, что...
• Теперь я могу...
• Я почувствовал, что...
• Я приобрел...
• Я научился...
• У меня получилось...
• Я смог...
• Я попробую...
|
|
Скачать 48.72 Kb.