шабло6н 7 класс. карточка-шаблон 7 класс. Теорема. Первый признак
 Скачать 133.46 Kb. Скачать 133.46 Kb.
|
|
Теорема. Первый признак: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.  Дано:△ABC и △A1B1C1 AC = A1C1 AB = A1B1 ∠A = ∠A1. Доказать: △ABC =△A1B1C1  Доказательство: Рассмотрим △A1B1C1 и △ABC AC = A1C1 AB = A1B1 ∠A = ∠A1. Следовательно, △ABC = △A1B1C1 по 1 признаку равенства треугольников. Теорема доказана. Теорема. Второй признак: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны  Дано:△ABC и △A1B1C1 AC = A1C1 ∠A = ∠A1 ∠C = ∠C1. Доказать: △ABC =△A1B1C1 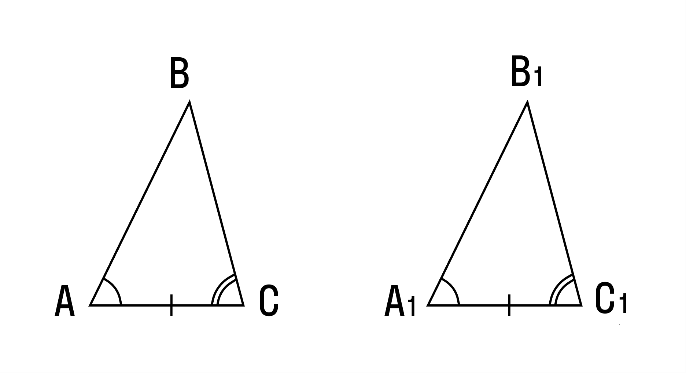 Доказательство: Рассмотрим △A1B1C1 и △ABC AC = A1C1 ∠A = ∠A1 ∠C = ∠C1. Следовательно, △ABC = △A1B1C1 по 2 признаку равенства треугольников. Теорема доказана. Теорема. Третий признак: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.  Дано:△ABC и △A1B1C1 AC = A1C1, AB = A1B1, CB = C1B1 Доказать: △ABC =△A1B1C1 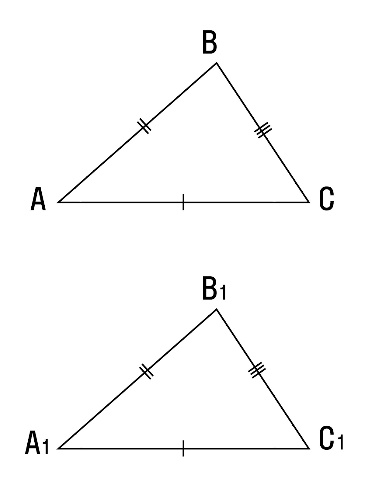 Доказательство: Рассмотрим △A1B1C1 и △ABC AC = A1C1 AB = A1B1, CB = C1B1 Следовательно, △ABC = △A1B1C1 по 3 признаку равенства треугольников. Теорема доказана. Теорема. Признак равенства треугольников по двум катетам: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.  Дано:△ABC и △A1B1C1 AC = A1C1 СB = С1B1 ∠С = ∠С1. Доказать: △ABC =△A1B1C1 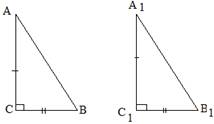 Доказательство: Рассмотрим △A1B1C1 и △ABC 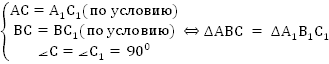 по двум катетам. по двум катетам.Теорема. Признак равенства треугольников по катету и прилежащему к нему углу: Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.  Дано:△ABC и △A1B1C1 AC = A1C1 ∠А = ∠А1. Доказать: △ABC =△A1B1C1 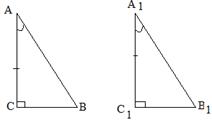 Доказательство: Рассмотрим △A1B1C1 и △ABC 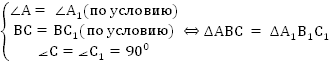 по катету и прилежащему острому углу. по катету и прилежащему острому углу. Дано:△ABC и △A1B1C1 AВ = A1В1 ∠В = ∠В1. Доказать: △ABC =△A1B1C1 Теорема. Признак равенства прямоугольных треугольников по гипотенузе и прилежащему острому углу: если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны.  Доказательство: Рассмотрим △A1B1C1 и △ABC ∠С=∠С1=90 градусов, следовательно, треугольники прямоугольные. АВ = А1В1 ( по условию), ∠В = ∠В1. Следовательно △ABC = △A1B1C1 по гипотенузе и острому углу. Теорема. Признак равенства прямоугольных треугольников по гипотенузе и катету: если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны.  Дано:△ABC и △A1B1C1 AВ = A1В1 АС = А1С1. Доказать: △ABC =△A1B1C1 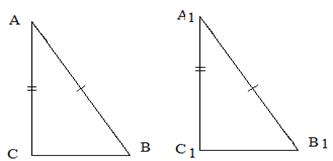 Доказательство: Рассмотрим △A1B1C1 и △ABC ∠С=∠С1=90 градусов, следовательно, треугольники прямоугольные. АВ = А1В1 ( по условию), АС=А1С1 (по условию). Следовательно, △ABC = △A1B1C1по гипотенузе и катету. Теорема. Признак равенства прямоугольных треугольников по катету и противолежащему углу: если катет и противолежащий ему острый угол одного прямоугольного треугольника равны соответственно катету и противолежащему ему острому углу другого прямоугольного треугольника, то такие треугольники равны.  Дано:△ABC и △A1B1C1 АС = А1С1. ∠В = ∠В1 Доказать: △ABC =△A1B1C1 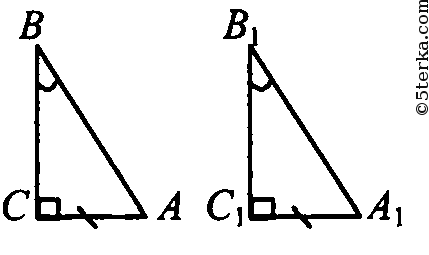 Доказательство: Рассмотрим △A1B1C1 и △ABC ∠С=∠С1=90 градусов, следовательно, треугольники прямоугольные. ∠В=∠В1 ( по условию), АС=А1С1 (по условию). Следовательно, △ABC = △A1B1C1по гипотенузе и катету. |
