критерий манна уитни. U критерий Манна-Уитни. Теоретическая часть Зачем нужен критерий МаннаУитни

• Название: Теоретическая часть Зачем нужен критерий МаннаУитни
• Анкор: критерий манна уитни
• Дата: 23.03.2021
• Размер: 48.15 Kb.
• Имя файла: U критерий Манна-Уитни.docx
• Тип: Документы; #187547

U- критерий Манна-Уитни

1. Теоретическая часть

2. Зачем нужен критерий Манна-Уитни

Как вы понимаете, в психологическом исследовании изучаются не результаты отдельных испытуемых, а обобщенные данные. Например, при изучении особенностей психологических параметров в двух группах изучаются средние значения в этих группах.

Напомню, что среднее (среднее арифметическое) отражает усредненный по группе показатель и рассчитывается среднее значение следующим образом:

• 
  Суммируются показатели у всех испытуемых в группе.
  
• 
  Сумма делиться на число испытуемых.
  

Таким образом, когда мы сравниваем психологические показатели у двух испытуемых, то никакие статистические критерии не нужны. Действительно, пусть в ходе тестирования уровень личностной тревожности Иванова оказался 40 баллов, а Петрова – 50 баллов. В этом случае мы смело говорим, что Петров более тревожен, чем Иванов. Но, если речь идет о сравнении двух групп, то ситуация усложняется.

Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. И как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?

Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.

Для анализа различий средних значений в двух группах используется t-критерий Стъюдента. И существует ещё U-критерий Манна-Уитни, который позволяет сравнивать не средние значения, а выраженность показателей. В этом случае и средние значения параметров в группах будут различаться соответствующим образом.

3. Расчет критерия Манна-Уитни: объяснение простыми словами

В подавляющем большинство психологических исследований расчет статистических критериев в том числе и критерия Манна-Уитни производится с помощью статистических программ. Наиболее известные – это SPSS и STATISTICA. Однако, несмотря на это важно в общих чертах представлять себе сущность расчета – это придаст большее понимание сути происходящего.

Вернёмся к примеру с тревожностью мужчин и женщин. Предположим у нас две группы по 10 человек. У каждого испытуемого есть определенное значение личностной тревожности. Нам нужно выяснить, различаются ли уровни тревожности в группах мужчин и женщин. Расчет критерия Манна-Уитни примерно будет проходить по следующим шагам:

1. 
   Показатели тревожности в группах заносятся в таблицу и ранжируются, то есть располагаются в порядке возрастания.
   
2. 
   Далее данные по мужчинам и женщинам объединяются в общий столбец (при этом они помечаются, например, разными цветом) и опять ранжируются.
   
3. 
   А далее проводится анализ. Если данные мужчин и женщин (синие и красные числа) в основном чередуются, то различий скорее всего нет.
   
4. 
   А вот если данные по мужчинам сгруппированы в основном вверху, где низкие показатели, а у женщин внизу, где высокие, то скорее всего различия есть.
   

Это, можно сказать, - объяснение на пальцах. Статистические программы, которыми мы к сожалению на данном этапе не обладаем, для расчета используют специальные алгоритмы, которые позволяют численно оценить эти пересечения данных обеих групп (синих и красных чисел) и сделать вывод о существовании или не существовании различий.

4. Что нужно знать про критерий Манна-Уитни, если вы им воспользуетесь на защите диплома

U-критерий Манна-Уитни – это непараметрический статистический критерий, использующийся для сравнения выраженности показателей в двух несвязных выборках.

Что такое непараметрический? Я напомню, что здесь нужно понимать следующее: Параметрические статистические критерии более точные, но они предъявляют более строгие требования к данным. То есть, перед расчетом нужно все данные в группах проверять, например, на нормальность распределения. Это значит, что на графике распределения такие данные должны располагаться в виде колокола – больше всего испытуемых со средними значениями, а меньшинство имеют низкие и высокие показатели. t-критерий Стъюдента, с которым вы уже знакомы, является параметрическим критерием.

Непараметрические критерии менее точные, но зато у них нет жестких требований к данным. Эти данные могут быть почти любыми.

Что значит несвязные выборки? Это означает, что группы не пресекаются, то есть в них разные испытуемые. Расчет различий в связных выборках используется, например, при выявлении эффективности тренингов, когда производятся замеры «до» и «после», а потом сравниваются. У критерия Стъюдента есть вариант для связных выборок. Критерий Манна-Уитни используется только для несвязных выборок.

5. Ограничения критерия Манна-Уитни

1. 
   Число испытуемых в группах при использовании критерия Манна-Уитни не должно быть больше 60 человек.
   
2. 
   Минимальное число испытуемых – 3 человека в каждой группе.
   
3. 
   Объем групп не должен быть строго одинаковым, но не должен сильно различаться.
   
4. 
   Сравниваемые показатели могут быть как психологическими (тревожность, агрессивность, самооценка и пр.), так и не психологическими (успешность обучения, эффективность профессиональной деятельности и пр.)
   

6. Если вам зададут вопрос: «Почему вы выбрали для расчета критерий Манна-Уитни, а не критерий Стьюдента?»

В качестве основы для индивидуальных модификаций предлагается следующий ответ:

«В данной работе не проверялись данные на нормальность распределения, поэтому использовался непараметрический статистический критерий Манна-Уитни, предназначенный для выявления различий показателей в двух несвязных выборках».

Важно понимать, что именно эти критерии наиболее часто используются для сравнительного анализа в психологических исследованиях. Но в их основе заложена значительная разница (параметрический и непараметрический). Поэтому в ответе и надо указать, что на нормальность данные не проверяли, например, из-за небольшого объема групп. Поэтому решили остановиться на непараметрическом критерии.

7. Уровень статистической значимости

Если вы будет пользоваться для расчета критерия Манна-Уитни статистической программой, то в выдаче результатов будут присутствовать два важных показателя:

1. 
   U – это, собственно, численное значение критерия. Для определения достоверности различий выраженности показателей в группах нужно сравнить полученное значение Uэмп с критическим значением из специальной таблицы – Uкр. Если Uэмп ≤ Uкр, то различия выраженности показателей в группах статистически значимы.
   
2. 
   р – уровень статистической значимости. Этот показатель присутствует при расчете всех статистических критериев и отражает степень точности вывода о наличие различий. Напоминаю, что в психологических исследованиях приняты два уровня точности:
   

• 
  р≤0,01 – вероятность ошибки 1%;
  
• 
  р≤0,05 – вероятность ошибки 5%.
  

8. Пример анализа данных с помощью критерия Манна-Уитни

Результаты сравнительного анализа показателей жизнестойкости

у молодежи и людей зрелого возраста

	Средние значения		U-критерий Манна-Уитни	Уровень статистической значимости (p)
	молодежь	люди зрелого возраста
Вовлеченность	32,9	40,9	673	0,000*
Контроль	27,2	28,3	1170,5	0,584
Принятие риска	17,9	14,4	686	0,000*
Жизнестойкость	78,0	83,6	1022,5	0,117

* - отмечены показатели, где различия статистически достоверны (р≤0,05 уровень статистической значимости 5%). Чем меньше Uэмп, тем более вероятно, что различия достоверны.

Анализ данных, приведенных в таблице по среднему показателю и по U-критерию, позволяет сделать следующие выводы:

Показатели по шкале «вовлеченность» в группе представителей старшего поколения статистически значимо выше, чем в группе представителей молодежи. Люди зрелого возраста характеризуются более высокой вовлеченностью в происходящее, они в большей степени получают удовольствие от собственной деятельности. В то же время молодежь в большей степени переживает чувство отвергнутости, ощущение себя «вне» жизни. Такой результат связан с психологическими особенностями возрастов: молодые люди еще не нашли своего места в жизни, это обуславливает их недостаточную вовлеченность в происходящее. Зрелые же люди в значительной степени укоренились в жизни, что позволяет им быть на более высоком уровне вовлеченности.

Показатели по шкале «принятие риска» в группе молодежи статистически значимо выше, чем в группе представителей зрелого возраста. Это означает, что молодые люди характеризуются более высокой убежденностью в том, что все то, что с ним случается, способствует его развитию за счет знаний, извлекаемых из опыта. Молодые в больше степени, чем зрелые люди, рассматривают жизнь как способ приобретения опыта, готовы действовать в отсутствие надежных гарантий успеха, на свой страх и риск, считая стремление к простому комфорту и безопасности обедняющим жизнь личности.

Как показывают полученные данные, различия показателей жизнестойкости в группах представителей молодежи и людей зрелого возраста не являются статистически значимыми, что в итоге предопределяет отсутствие различий в общем показателей жизнестойкости в группах испытуемых.

Различия показателей жизнестойкости в группах представителей молодого поколения и людей зрелого возраста носят разнонаправленный характер, так как зона пересечения показателей, что оценивает U-критерий, у этих групп незначительная, и это говорит о том, что у молодежи в большей степени выражено принятие риска, а у людей зрелого возраста – вовлеченность в происходящее.
Практическая часть

Назначение критерия. Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n₁,n₂ ≥3 или n₁= 2, n₂ ≥ 5, и является более мощным, чем критерий Q Розенбаума.

Описание критерия. Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1ым рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2ым рядом — тот, где они предположительно ниже.

Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок. Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше U_эмп, тем более вероятно, что различия достоверны.

9. Гипотезы.

Н0: Уровень признака в группе 2 не ниже уровня признака в группе 1.

Н1: Уровень признака в группе 2 ниже уровня признака в группе 1.

Некоторые возможные представление критерия U.

Рассмотрим три из множества возможных вариантов соотношения двух рядов значений.

а). 2й ряд ниже первого, но ряды почти не перекрещиваются. Область наложения слишком мала (они практически различны и количество совпадений очень мало), чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.

б). 2ой ряд тоже ниже первого, но область перекрещивающихся значений у двух рядов достаточно обширна. Она может еще не достигать критической величины, когда различия придется признать несущественными. Но так ли это, можно определить только путем точного подсчета критерия U.

в). 2ой ряд ниже первого, но область наложения настолько обширна, что различия между рядами скрадываются.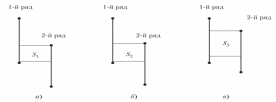



Ограничения критерия U.

1. 
   В каждой выборке должно быть не менее 3 наблюдений: n_1, п₂≥ 3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во 2ой их должно быть не менее 5.
   
2. 
   В каждой выборке должно быть не более 60 наблюдений; п₁, п₂ ≤ 60. Однако уже при
   

n_1, п₂ > 20 ранжирование становится достаточно трудоемким. Если группы большего объема, то лучше использовать t-критерий Стъюдента.

Пример

Рассмотрим результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения невербального интеллекта.

Данные приведены в таблице 1.

Таблица 1.

Индивидуальные значения невербального интеллекта

в выборках студентов физического (n1=14)

и психологического (n2=12) факультетов

Студенты-физики		Студенты-психологи
Код имени испытуемого	Показатель невербального интеллекта	Код имени испытуемого	Показатель невербального интеллекта
1. И. А.	111	1. Н. Т.	113
2. К А.	104	2. О. В.	107
3. К. Е.	107	3. Е. В.	123
4. П. А.	90	4. Ф. О.	122
5. С.А.	115	5, И. Н.	117
6. Ст. А.	107	6. И. Ч.	112
7. Т. Л.	106	7. И. В.	105
8. Ф. А.	107	8. К. О.	108
9. Ч. И.	95	9. Р. Р.	111
10. Ц. А.	116	10. Р. И.	114
11. См. А.	127	11. О. К.	102
12. К. Ан.	115	12. Н. К.	104
13. Б. Л.	102
14. Ф. В.	99

Критерий U требует тщательности и внимания. Прежде всего, необходимо помнить правила ранжирования.

Правила ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.

Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг: (1+2+3)/3 = 6/3 = 2

Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг: (4+5)/2 = 9/2 = 4,5 и т.д.

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:

Σ (Ri) = N * (N+1) / 2

где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.

АЛГОРИТМ

Подсчет критерия U Манна-Уитни.

Мы проведем расчеты вручную, так как этот навык поможет вам справиться с задачей в ситуации, если у вас нет компьютера, снабженного статистическим пакетом (что собственно в моем случае является реальностью).

1. Перенести все данные испытуемых на индивидуальные карточки.

2. Пометить карточки испытуемых выборки 1 одним цветом, скажем, красным, а все карточки из выборки 2 - другим, например, синим.

3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.

4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Всего рангов получится столько, сколько у нас испытаний ( n₁ +п₂ ).

5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.

6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.

7. Определить большую из двух ранговых сумм.

8. Определить значение Uэмп. по формуле:

Uэмп. = (n1 * n2) + (nx * ( nx +1)) / - Tx

где n₁ - количество испытуемых в выборке 1;

n₂ - количество испытуемых в выборке 2;

Т_х - бОльшая из двух ранговых сумм;

n_х - количество испытуемых в группе с бОльшей суммой рангов.

9. Определить критические значения U по таблице «Критические значения критерия U Манна-Уитни для уровней статистической значимости p ≤ 0,05 и p≤ 0,01 (по Гублеру Е.В., Генкину А.А., 1973)».

Если Uэмп. >Uкp 005, Но принимается. Если Uэмп≤Uкp_005, Но отвергается.

Чем меньше значения U, тем достоверность различий выше.

Теперь проделаем всю эту работу на материале данного примера. В результате работы по 1-6 шагам алгоритма построим таблицу.

Таблица 2.

Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов

Студенты-физики (n1=14)			Студенты-психологи (n2=12)
Показатель невербального интеллекта		Ранг	Показатель невербального интеллекта	Ранг
127		26
			123	25
			122	24
			117	23
116		22
115		20,5
115		20,5
			114	19
			113	18
			112	17
111		15,5	111	15.5
			108	14'
107		11.5	107	11,5
107		11,5
107		11,5
106		9
			105	8
104		6.5	104	6,5
102		4,5	102	4,5
99		3
95		2
90		1
Суммы	1501	165	1338	186
Средние	107,2		111,5

Общая сумма рангов: 165+186=351. Расчетная сумма:

Σ (Ri) = N * (N+1) / 2 = 26 * (26+1) / 2 = 351. Равенство реальной и расчетной сумм соблюдено.

Мы видим, что по уровню невербального интеллекта более "высоким" рядом оказывается выборка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186.

Теперь можно сформулировать гипотезы:

H₀: Группа студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта.

Н₁: Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта.

В соответствии со следующим шагом алгоритма определяем эмпирическую величину Uэмп.:

Uэмп. = (n1 * n2) + (nx * ( nx +1)) / 2 - Tx , где напомню: Т_х - бОльшая из двух ранговых сумм;

n_х - количество испытуемых в группе с большей суммой рангов.

(14 * 12) + (12 * (12+1)) / 2 — 186 = 60

Поскольку в нашем случае п1≠ п2, подсчитаем эмпирическую величину Uэмп. и для второй ранговой суммы (165), подставляя в формулу соответствующее ей п_х:

Uэмп. = (n1 * n2) + (nx * ( nx +1)) / - Tx = (14 * 12) + (14 * (14+1)) / 2 — 165 = 108

Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982; Greene J., D'Olivera M., 1989).

Для сопоставления с критическим значением выбираем меньшую величину U: U_эмп=60.

По таблице «Критические значения критерия U Манна-Уитни для уровней статистической значимости p ≤ 0,05 и p≤ 0,01 (по Гублеру Е.В., Генкину А.А., 1973)» определяем критические значения для соответствующих n . Причем меньшее n принимаемза

n₁ =12 и отыскиваем его вверхней строке таблицы. Большее n принимаем за n₂ =14 и находим слева.

Uкр = 51 ( p ≤ 0,05) и Uкр = 38 (p≤ 0,01)

Мы помним, что критерий U является одним из двух исключений из общего правила принятия решения о достоверности различий, а именно, мы можем констатировать достоверные различия, если U_эмп ≤ U_кp

Расположим на "оси значимости" в порядке возрастания полученные значения U.

U_0,01=38 U_0,05=51 U_эмп=60

U_эмп>U_кp

Ответ: H₀ принимается. Группа студентов-психологов не превосходит группы студентов-физиков по уровню невербального интеллекта.

Обратим внимание на то, что для данного случая критерий Q Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в группе психологов: и самое высокое, и самое низкое значение невербального интеллекта приходится на группу физиков (см. Табл.2).